besseli
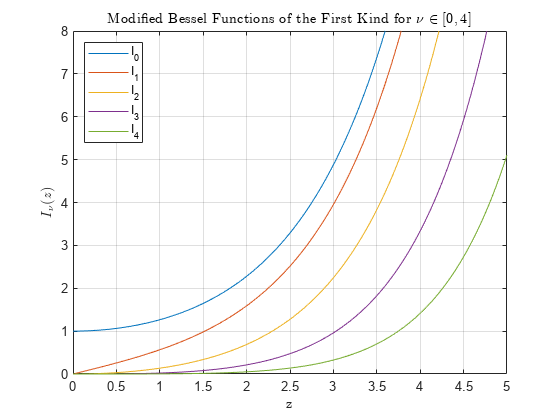
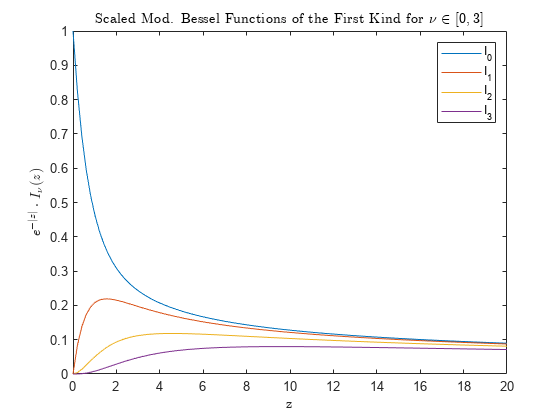
Modified Bessel function of first kind
Description
I = besseli(
computes the modified Bessel function of the first kind
Iν(z) for each element in array nu,Z)Z.
Examples
Input Arguments
More About
References
[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.
Extended Capabilities
Version History
Introduced before R2006a