Filter Data
Filter Difference Equation
Filters are data processing
techniques that can smooth out high-frequency fluctuations in data
or remove periodic trends of a specific frequency from data. In MATLAB®,
the filter function filters
a vector of data x according to the following difference
equation, which describes a tapped delay-line filter.
In this equation, a and b are vectors of coefficients of the filter, Na is the feedback filter order, and Nb is the feedforward filter order. n is the index of the current element of x. The output y(n) is a linear combination of the current and previous elements of x and y.
The filter function uses specified coefficient
vectors a and b to filter the
input data x. For more information on difference
equations describing filters, see [1].
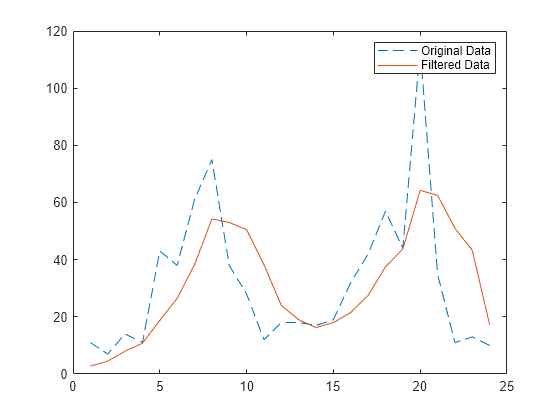
Moving-Average Filter of Traffic Data
The filter function is one way to implement a moving-average filter, which is a common data smoothing technique.
The following difference equation describes a filter that averages time-dependent data with respect to the current hour and the three previous hours of data.
Import data that describes traffic flow over time, and assign the first column of vehicle counts to the vector x.
load count.dat
x = count(:,1);Create the filter coefficient vectors.
a = 1; b = [1/4 1/4 1/4 1/4];
Compute the 4-hour moving average of the data, and plot both the original data and the filtered data.
y = filter(b,a,x); t = 1:length(x); plot(t,x,'--',t,y,'-') legend('Original Data','Filtered Data')
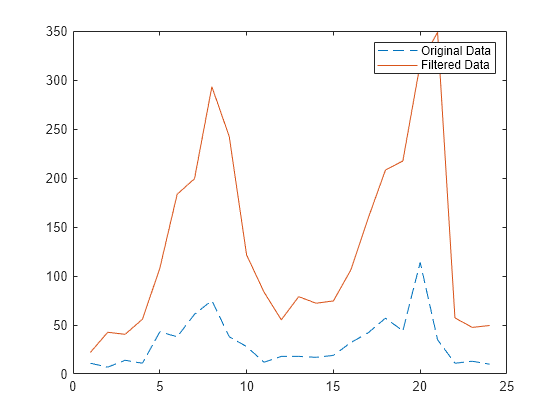
Modify Amplitude of Data
This example shows how to modify the amplitude of a vector of data by applying a transfer function.
In digital signal processing, filters are often represented by a transfer function. The Z-transform of the difference equation
is the following transfer function.
Use the transfer function
to modify the amplitude of the data in count.dat.
Load the data and assign the first column to the vector x.
load count.dat
x = count(:,1);Create the filter coefficient vectors according to the transfer function .
a = [1 0.2]; b = [2 3];
Compute the filtered data, and plot both the original data and the filtered data. This filter primarily modifies the amplitude of the original data.
y = filter(b,a,x); t = 1:length(x); plot(t,x,'--',t,y,'-') legend('Original Data','Filtered Data')
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999.
See Also
filter | conv | filter2 | smoothdata | movmean