smoothdata
Smooth noisy data
Syntax
Description
B = smoothdata(A)A using a moving average.
smoothdata determines the moving window size from the
entries in A. The window slides down the length of the
vector, computing an average over the elements within each window.
If
Ais a matrix, thensmoothdatacomputes the moving average down each column ofA.If
Ais a multidimensional array, thensmoothdataoperates along the first dimension ofAwhose size does not equal 1.If
Ais a table or timetable with numeric variables, thensmoothdataoperates on each variable ofAseparately.
B = smoothdata(___,Name,Value)t is a vector of time values, then
smoothdata(A,"SamplePoints",t) smooths the data in
A relative to the times in t.
[ also returns the moving window size.B,winsize]
= smoothdata(___)
Alternative
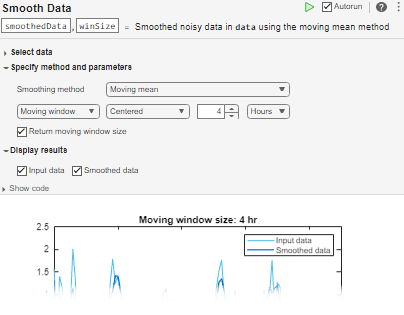
You can use smoothdata functionality interactively by
adding the Smooth
Data task to a live script.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
When the window size for the smoothing method is not specified, smoothdata computes
a default window size based on a heuristic. For a smoothing factor τ,
the heuristic estimates a moving average window size that attenuates
approximately 100*τ percent of the energy of the input data.
Extended Capabilities
Version History
Introduced in R2017aSee Also
Functions
smoothdata2|fillmissing|fillmissing2|movmean|movmedian|movmad|filter









![Given elements 1 to 7, if the current sample point is 4, then the corresponding window spans the range [2, 6].](movwindow_vector.png)
![Given elements 1 to 7, if the current sample point is 2, then the corresponding window spans the range [1, 4].](movwindow_edgetruncate.png)
![Given elements 1 to 7, if the current sample point is 2, then the corresponding window spans the range [1, 5].](movwindow_edgeslide.png)