Vanilla
Vanilla instrument object
Description
Create and price a Vanilla instrument object for one or
more Vanilla instruments using this workflow:
Use
fininstrumentto create aVanillainstrument object for one or more Vanilla instruments.Use
finmodelto specify aBlackScholes,Bachelier,Heston,Bates,Merton,RoughBergomi,RoughHeston, orDupiremodel for theVanillainstrument object.Choose a pricing method.
When using a
BlackScholesmodel, usefinpricerto specify aFiniteDifference,BlackScholes,BjerksundStensland,RollGeskeWhaley,VannaVolga,AssetTree, orAssetMonteCarlopricing method for one or moreVanillainstruments.When using a
Heston,Bates, orMertonmodel, usefinpricerto specify aFiniteDifference,NumericalIntegration,FFT, orAssetMonteCarlopricing method for one or moreVanillainstruments.When using a
Dupiremodel, usefinpricerto specify aFiniteDifferencepricing method for one or moreVanillainstruments.When using a
Bacheliermodel, usefinpricerto specify anAssetMonteCarlopricing method for one or moreVanillainstruments.When using a
RoughBergomiorRoughHestonmodel, usefinpricerto specify aRoughVolMonteCarlopricing method for one or moreVanillainstruments.
For more information on this workflow, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.
For more information on the available models and pricing methods for a
Vanilla instrument, see Choose Instruments, Models, and Pricers.
Creation
Syntax
Description
VanillaObj = fininstrument(InstrumentType,'Strike',strike_value,'ExerciseDate',exercise_date)Vanilla object for one or more Vanilla
instruments by specifying InstrumentType and sets the
properties for the
required name-value pair arguments Strike and
ExerciseDate. For more information on a
Vanilla instrument, see More About.
VanillaObj = fininstrument(___,Name,Value)VanillaObj =
fininstrument("Vanilla",'Strike',100,'ExerciseDate',datetime(2019,1,30),'OptionType',"put",'ExerciseStyle',"American",'Name',"vanilla_instrument")
creates a Vanilla put option with an American exercise.
You can specify multiple name-value pair arguments.
Input Arguments
Instrument type, specified as a string with the value of
"Vanilla", a character vector with the value of
'Vanilla', an
NINST-by-1 string array with
values of "Vanilla", or an
NINST-by-1 cell array of
character vectors with values of 'Vanilla'.
Data Types: char | cell | string
Name-Value Arguments
Specify required
and optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where
Name is the argument name and Value is
the corresponding value. Name-value arguments must appear after other arguments,
but the order of the pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: VanillaObj =
fininstrument("Vanilla",'Strike',100,'ExerciseDate',datetime(2019,1,30),'OptionType',"put",'ExerciseStyle',"American",'Name',"vanilla_instrument")
Required Vanilla Name-Value Pair Arguments
Option strike price value, specified as the comma-separated pair
consisting of 'Strike' and a scalar nonnegative
numeric value or an NINST-by-1
nonnegative numeric vector.
Note
When using a "Bermudan"
ExerciseStyle with a FiniteDifference pricer, the
Strike is a vector.
Data Types: double
Option exercise date, specified as the comma-separated pair
consisting of 'ExerciseDate' and a scalar or an
NINST-by-1 vector using a
datetime array, string array, or date character vectors.
Note
For a European option, there is only one
ExerciseDate on the option expiry
date.
When using a "Bermudan"
ExerciseStyle with a FiniteDifference pricer, the
ExerciseDate is a vector.
To support existing code, Vanilla also
accepts serial date numbers as inputs, but they are not recommended.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the ExerciseDate property is stored as a
datetime.
Optional Vanilla Name-Value Pair Arguments
Option type, specified as the comma-separated pair consisting of
'OptionType' and a scalar string or character
vector or an NINST-by-1 cell
array of character vectors or string array.
A call option gives the holder the right to buy the underlying asset at the strike price, while a put option gives the holder the right to sell the underlying asset at the strike price.
Note
When you use a RollGeskeWhaley pricer with a
Vanilla option,
OptionType must be
'call'.
Data Types: char | cell | string
Option exercise style, specified as the comma-separated pair
consisting of 'ExerciseStyle' and a scalar string
or character vector or an
NINST-by-1 cell array of
character vectors or string array.
Note
When you use a
BlackScholespricer with aVanillaoption, the'American'option type is not supported.When you use a
RollGeskeWhaleyor aBjerksundStenslandpricer with aVanillaoption, you must specify an'American'option.When you use a
NumericalIntegrationpricer with aBates,Merton, orHestonmodel for aVanillaoption, theExerciseStylemust be'European'.When you use a
FFTpricer with aBates,Merton, orHestonmodel for aVanillaoption, theExerciseStylemust be'European'.When you use an
AssetMonteCarlopricer with aBlackScholes,Bates,Merton, orHestonmodel for aVanillaoption, theExerciseStylecan be'American','European', or'Bermudan'.When you use a
FiniteDifferencepricer with aBlackScholes,Bachelier,Dupire,Bates,Merton, orHestonmodel for aVanillaoption, theExerciseStylecan be'American','European', or'Bermudan'.
For more information on
ExerciseStyle, see Supported Exercise Styles.
Data Types: string | cell | char
User-defined name for one of more instruments, specified as the
comma-separated pair consisting of 'Name' and a
scalar string or character vector or an
NINST-by-1 cell array of
character vectors or string array.
Data Types: char | cell | string
Output Arguments
Vanilla instrument, returned as a Vanilla
object.
Properties
Option strike price value, returned as a scalar nonnegative numeric or an
NINST-by-1 nonnegative numeric
vector.
Data Types: double
Option exercise date, returned as a scalar datetime or an
NINST-by-1 vector of
datetimes.
Data Types: datetime
Option type, returned as a scalar string or an
NINST-by-1 string array with
values of "call" or "put".
Data Types: string
Option exercise style, returned as a scalar string or an
NINST-by-1 string array with
values of "European", "American", or
"Bermudan".
Data Types: string
User-defined name for the instrument, returned as a scalar string or an
NINST-by-1 string array.
Data Types: string
Object Functions
setExercisePolicy | Set exercise policy for FixedBondOption,
FloatBondOption, or Vanilla instrument |
Examples
This example shows the workflow to price a Vanilla instrument when you use a BlackScholes model and a BlackScholes pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2018,5,1),'Strike',29,'OptionType',"put",'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "put"
ExerciseStyle: "european"
ExerciseDate: 01-May-2018
Strike: 29
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes",'Volatility',0.25)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2500
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,1,1); Maturity = datetime(2019,1,1); Rate = 0.05; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',1)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 1
Dates: 01-Jan-2019
Rates: 0.0500
Settle: 01-Jan-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create BlackScholes Pricer Object
Use finpricer to create a BlackScholes pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'DiscountCurve',myRC,'Model',BlackScholesModel,'SpotPrice',30,'DividendValue',0.045)
outPricer =
BlackScholes with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 30
DividendValue: 0.0450
DividendType: "continuous"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 1.2046
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: []
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Vega Rho Theta
______ ________ ________ _______ ______ _______ _______
1.2046 -0.36943 0.086269 -9.3396 6.4702 -4.0959 -2.3107
This example shows the workflow to price multiple Vanilla instrument when you use a BlackScholes model and a BlackScholes pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object for three Vanilla instruments.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime([2018,5,1 ; 2018,6,1 ; 2018,7,1]),'Strike',[29 ; 38 ; 70],'OptionType',"put",'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt=3×1 Vanilla array with properties:
OptionType
ExerciseStyle
ExerciseDate
Strike
Name
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes",'Volatility',0.25)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2500
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,1,1); Maturity = datetime(2019,1,1); Rate = 0.05; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',1)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 1
Dates: 01-Jan-2019
Rates: 0.0500
Settle: 01-Jan-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create BlackScholes Pricer Object
Use finpricer to create a BlackScholes pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'DiscountCurve',myRC,'Model',BlackScholesModel,'SpotPrice',30,'DividendValue',0.045)
outPricer =
BlackScholes with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 30
DividendValue: 0.0450
DividendType: "continuous"
Price Vanilla Instruments
Use price to compute the prices and sensitivities for the Vanilla instruments.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 3×1
1.2046
7.9479
38.9392
outPR=3×1 priceresult array with properties:
Results
PricerData
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Vega Rho Theta
______ ________ ________ _______ ______ _______ _______
1.2046 -0.36943 0.086269 -9.3396 6.4702 -4.0959 -2.3107
ans=1×7 table
Price Delta Gamma Lambda Vega Rho Theta
______ ________ ________ _______ ______ _______ _______
7.9479 -0.89786 0.031587 -3.4532 2.9612 -14.535 -0.3563
ans=1×7 table
Price Delta Gamma Lambda Vega Rho Theta
______ ________ __________ ________ __________ _______ ______
38.939 -0.97775 1.2279e-06 -0.77043 0.00013814 -34.136 2.0936
This example shows the workflow to price a Vanilla instrument when you use a BlackScholes model and an AssetTree pricing method using a Leisen-Reimer (LR) binomial tree.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2018,5,1),'Strike',29,'OptionType',"put",'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "put"
ExerciseStyle: "european"
ExerciseDate: 01-May-2018
Strike: 29
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes",'Volatility',0.25)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2500
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,1,1); Maturity = datetime(2019,1,1); Rate = 0.05; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',1)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 1
Dates: 01-Jan-2019
Rates: 0.0500
Settle: 01-Jan-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create AssetTree Pricer Object
Use finpricer to create an AssetTree pricer object for a LR equity tree and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
NumPeriods = 15; LRPricer = finpricer("AssetTree",'DiscountCurve',myRC,'Model',BlackScholesModel,'SpotPrice',50,'PricingMethod',"LeisenReimer",'Maturity',datetime(2018,5,1),'NumPeriods',NumPeriods)
LRPricer =
LRTree with properties:
InversionMethod: PP1
Strike: 50
Tree: [1×1 struct]
NumPeriods: 15
Model: [1×1 finmodel.BlackScholes]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 50
DividendType: "continuous"
DividendValue: 0
TreeDates: [09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
LRPricer.Tree
ans = struct with fields:
Probs: [2×15 double]
ATree: {1×16 cell}
dObs: [01-Jan-2018 09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
tObs: [0 0.0222 0.0444 0.0667 0.0889 0.1111 0.1333 0.1556 0.1778 0.2000 0.2222 0.2444 0.2667 0.2889 0.3111 0.3333]
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(LRPricer,VanillaOpt,["all"])Price = 3.5022e-06
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Vega Lambda Rho Theta
__________ ___________ __________ _________ _______ ___________ ___________
3.5022e-06 -1.9331e-06 1.1068e-06 0.0016243 -30.496 -3.6747e-05 -0.00060106
outPR.PricerData.PriceTree
ans = struct with fields:
PTree: {1×16 cell}
ExTree: {1×16 cell}
tObs: [0 0.0222 0.0444 0.0667 0.0889 0.1111 0.1333 0.1556 0.1778 0.2000 0.2222 0.2444 0.2667 0.2889 0.3111 0.3333]
dObs: [01-Jan-2018 09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
Probs: [2×15 double]
outPR.PricerData.PriceTree.ExTree
ans=1×16 cell array
{[0]} {[0 0]} {[0 0 0]} {[0 0 0 0]} {[0 0 0 0 0]} {[0 0 0 0 0 0]} {[0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]}
This example shows the workflow to price a Vanilla instrument when you use a BlackScholes model and an AssetTree pricing method using a Standard Trinomial (STT) tree.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2018,5,1),'Strike',29,'OptionType',"put",'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "put"
ExerciseStyle: "european"
ExerciseDate: 01-May-2018
Strike: 29
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes",'Volatility',0.25)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2500
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,1,1); Maturity = datetime(2019,1,1); Rate = 0.05; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',1)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 1
Dates: 01-Jan-2019
Rates: 0.0500
Settle: 01-Jan-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create AssetTree Pricer Object
Use finpricer to create an AssetTree pricer object for a Standard Trinomial (STT) equity tree and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
NumPeriods = 15; STTPricer = finpricer("AssetTree",'DiscountCurve',myRC,'Model',BlackScholesModel,'SpotPrice',50,'PricingMethod',"StandardTrinomial",'Maturity',datetime(2018,5,1),'NumPeriods',NumPeriods)
STTPricer =
STTree with properties:
Tree: [1×1 struct]
NumPeriods: 15
Model: [1×1 finmodel.BlackScholes]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 50
DividendType: "continuous"
DividendValue: 0
TreeDates: [09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
STTPricer.Tree
ans = struct with fields:
ATree: {1×16 cell}
Probs: {[3×1 double] [3×3 double] [3×5 double] [3×7 double] [3×9 double] [3×11 double] [3×13 double] [3×15 double] [3×17 double] [3×19 double] [3×21 double] [3×23 double] [3×25 double] [3×27 double] [3×29 double]}
dObs: [01-Jan-2018 09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
tObs: [0 0.0222 0.0444 0.0667 0.0889 0.1111 0.1333 0.1556 0.1778 0.2000 0.2222 0.2444 0.2667 0.2889 0.3111 0.3333]
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(STTPricer,VanillaOpt,["all"])Price = 6.3773e-05
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Vega Lambda Rho Theta
__________ ___________ __________ _________ _______ ___________ _________
6.3773e-05 -9.1432e-06 1.2388e-06 0.0034421 -21.514 -0.00064994 -0.001188
outPR.PricerData.PriceTree
ans = struct with fields:
PTree: {1×16 cell}
ExTree: {1×16 cell}
tObs: [0 0.0222 0.0444 0.0667 0.0889 0.1111 0.1333 0.1556 0.1778 0.2000 0.2222 0.2444 0.2667 0.2889 0.3111 0.3333]
dObs: [01-Jan-2018 09-Jan-2018 17-Jan-2018 25-Jan-2018 02-Feb-2018 10-Feb-2018 18-Feb-2018 26-Feb-2018 06-Mar-2018 14-Mar-2018 22-Mar-2018 30-Mar-2018 07-Apr-2018 15-Apr-2018 23-Apr-2018 01-May-2018]
Probs: {[3×1 double] [3×3 double] [3×5 double] [3×7 double] [3×9 double] [3×11 double] [3×13 double] [3×15 double] [3×17 double] [3×19 double] [3×21 double] [3×23 double] [3×25 double] [3×27 double] [3×29 double]}
outPR.PricerData.PriceTree.ExTree
ans=1×16 cell array
{[0]} {[0 0 0]} {[0 0 0 0 0]} {[0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]} {[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1]}
This example shows the workflow to price an American option for a Vanilla instrument when you use a BlackScholes model and a RollGeskeWhaley pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'Strike',105,'ExerciseDate',datetime(2022,9,15),'OptionType',"call",'ExerciseStyle',"american",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "american"
ExerciseDate: 15-Sep-2022
Strike: 105
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes","Volatility",0.2)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2000
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create RollGeskeWhaley Pricer Object
Use finpricer to create a RollGeskeWhaley pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'Model',BlackScholesModel,'DiscountCurve',myRC,'SpotPrice',100,'DividendValue',timetable(datetime(2021,6,15),0.25),'PricingMethod',"RollGeskeWhaley")
outPricer =
RollGeskeWhaley with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 100
DividendValue: [1×1 timetable]
DividendType: "cash"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 19.9066
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: []
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Vega Theta Rho
______ _______ _________ ______ ______ _______ ______
19.907 0.66568 0.0090971 3.344 72.804 -3.4537 186.68
This example shows the workflow to price a Vanilla instrument for foreign exchange (FX) when you use a BlackScholes model and a BlackScholes pricing method. Assume that the current exchange rate is $0.52 and has a volatility of 12% per annum. The annualized continuously compounded foreign risk-free rate is 8% per annum.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2022,9,15),'Strike',.50,'OptionType',"put",'ExerciseStyle',"european",'Name',"vanilla_fx_option")
VanillaOpt =
Vanilla with properties:
OptionType: "put"
ExerciseStyle: "european"
ExerciseDate: 15-Sep-2022
Strike: 0.5000
Name: "vanilla_fx_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
Sigma = .12; BlackScholesModel = finmodel("BlackScholes","Volatility",Sigma)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.1200
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create BlackScholes Pricer Object
Use finpricer to create a BlackScholes pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument. When pricing currencies using a Vanilla instrument, the DividendType must be 'continuous' and DividendValue is the annualized risk-free interest rate in the foreign country.
ForeignRate = 0.08; outPricer = finpricer("analytic",'DiscountCurve',myRC,'Model',BlackScholesModel,'SpotPrice',.52,'DividendType',"continuous",'DividendValue',ForeignRate)
outPricer =
BlackScholes with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 0.5200
DividendValue: 0.0800
DividendType: "continuous"
Price Vanilla FX Instrument
Use price to compute the price and sensitivities for the Vanilla FX instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 0.0738
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: []
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Vega Rho Theta
________ ________ ______ _______ _______ _______ _________
0.073778 -0.49349 2.0818 -4.7899 0.27021 -1.3216 -0.013019
This example shows the workflow to price an American option for a Vanilla instrument when you use a BlackScholes model and an AssetMonteCarlo pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'Strike',105,'ExerciseDate',datetime(2022,9,15),'OptionType',"call",'ExerciseStyle',"american",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "american"
ExerciseDate: 15-Sep-2022
Strike: 105
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes","Volatility",0.2)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2000
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create AssetMonteCarlo Pricer Object
Use finpricer to create an AssetMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("AssetMonteCarlo",'DiscountCurve',myRC,"Model",BlackScholesModel,'SpotPrice',150,'simulationDates',datetime(2022,9,15))
outPricer =
GBMMonteCarlo with properties:
DiscountCurve: [1×1 ratecurve]
SpotPrice: 150
SimulationDates: 15-Sep-2022
NumTrials: 1000
RandomNumbers: []
Model: [1×1 finmodel.BlackScholes]
DividendType: "continuous"
DividendValue: 0
MonteCarloMethod: "standard"
BrownianMotionMethod: "standard"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 61.2010
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Rho Theta Vega
______ _______ _________ ______ ______ _______ ______
61.201 0.93074 0.0027813 2.2812 313.95 -3.7909 41.626
This example shows the workflow to price an American option for a Vanilla instrument when you use a BlackScholes model and an AssetMonteCarlo pricing method with quasi-Monte Carlo simulation.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'Strike',105,'ExerciseDate',datetime(2022,9,15),'OptionType',"call",'ExerciseStyle',"american",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "american"
ExerciseDate: 15-Sep-2022
Strike: 105
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes","Volatility",0.2)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2000
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create AssetMonteCarlo Pricer Object
Use finpricer to create an AssetMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value argument and the name-value arguments for MonteCarloMethod and BrownianMotionMethod.
outPricer = finpricer("AssetMonteCarlo",'DiscountCurve',myRC,"Model",BlackScholesModel,'SpotPrice',150,'simulationDates',datetime(2022,9,15),'NumTrials',1e3, ... 'MonteCarloMethod',"quasi",'BrownianMotionMethod',"brownian-bridge")
outPricer =
GBMMonteCarlo with properties:
DiscountCurve: [1×1 ratecurve]
SpotPrice: 150
SimulationDates: 15-Sep-2022
NumTrials: 1000
RandomNumbers: []
Model: [1×1 finmodel.BlackScholes]
DividendType: "continuous"
DividendValue: 0
MonteCarloMethod: "quasi"
BrownianMotionMethod: "brownian-bridge"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,"all")Price = 60.7272
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Rho Theta Vega
______ _______ _________ ______ ______ _______ ______
60.727 0.92248 0.0024038 2.2786 310.66 -3.7073 39.466
This example shows the workflow to price an American option for a Vanilla instrument when you use a Heston model and an AssetMonteCarlo pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'Strike',105,'ExerciseDate',datetime(2022,9,15),'OptionType',"call",'ExerciseStyle',"american",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "american"
ExerciseDate: 15-Sep-2022
Strike: 105
Name: "vanilla_option"
Create Heston Model Object
Use finmodel to create a Heston model object.
HestonModel = finmodel("Heston",'V0',0.032,'ThetaV',0.07,'Kappa',0.003,'SigmaV',0.02,'RhoSV',0.09)
HestonModel =
Heston with properties:
V0: 0.0320
ThetaV: 0.0700
Kappa: 0.0030
SigmaV: 0.0200
RhoSV: 0.0900
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create AssetMonteCarlo Pricer Object
Use finpricer to create an AssetMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("AssetMonteCarlo",'DiscountCurve',myRC,"Model",HestonModel,'SpotPrice',150,'simulationDates',datetime(2022,9,15))
outPricer =
HestonMonteCarlo with properties:
DiscountCurve: [1×1 ratecurve]
SpotPrice: 150
SimulationDates: 15-Sep-2022
NumTrials: 1000
RandomNumbers: []
Model: [1×1 finmodel.Heston]
DividendType: "continuous"
DividendValue: 0
MonteCarloMethod: "standard"
BrownianMotionMethod: "standard"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 60.5637
outPR =
priceresult with properties:
Results: [1×8 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×8 table
Price Delta Gamma Lambda Rho Theta Vega VegaLT
______ _______ _________ ______ ______ _______ ______ _______
60.564 0.94774 0.0011954 2.3473 326.36 -3.7126 35.272 0.31155
This example shows the workflow to price a Bermudan option for a Vanilla instrument when you use a BlackScholes model and a FiniteDifference pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'Strike',[110,120],'ExerciseDate',[datetime(2022,9,15) , datetime(2023,9,15)],'OptionType',"call",'ExerciseStyle',"Bermudan",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "bermudan"
ExerciseDate: [15-Sep-2022 15-Sep-2023]
Strike: [110 120]
Name: "vanilla_option"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
BlackScholesModel = finmodel("BlackScholes","Volatility",0.2)
BlackScholesModel =
BlackScholes with properties:
Volatility: 0.2000
Correlation: 1
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create FiniteDifference Pricer Object
Use finpricer to create a FiniteDifference pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("FiniteDifference",'Model',BlackScholesModel,'DiscountCurve',myRC,'SpotPrice',100)
outPricer =
FiniteDifference with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 100
GridProperties: [1×1 struct]
DividendType: "continuous"
DividendValue: 0
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,["all"])Price = 18.6797
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Theta Rho Vega
_____ _______ _________ ______ _______ ______ ______
18.68 0.62163 0.0091406 3.3278 -3.3154 184.31 83.162
This example shows the workflow to price a Vanilla instrument when you use a Heston model and various pricing methods.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle,6); Strike = 80; VanillaOpt = fininstrument('Vanilla','ExerciseDate',Maturity,'Strike',Strike,'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 29-Dec-2017
Strike: 80
Name: "vanilla_option"
Create Heston Model Object
Use finmodel to create a Heston model object.
V0 = 0.04; ThetaV = 0.05; Kappa = 1.0; SigmaV = 0.2; RhoSV = -0.7; HestonModel = finmodel("Heston",'V0',V0,'ThetaV',ThetaV,'Kappa',Kappa,'SigmaV',SigmaV,'RhoSV',RhoSV)
HestonModel =
Heston with properties:
V0: 0.0400
ThetaV: 0.0500
Kappa: 1
SigmaV: 0.2000
RhoSV: -0.7000
Create ratecurve object
Create a ratecurve object using ratecurve.
Rate = 0.03;
ZeroCurve = ratecurve('zero',Settle,Maturity,Rate);Create NumericalIntegration, FFT, and FiniteDifference Pricer Objects
Use finpricer to create a NumericalIntegration, FFT, and FiniteDifference pricer objects and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
SpotPrice = 80; Strike = 80; DividendYield = 0.02; NIPricer = finpricer("NumericalIntegration",'Model', HestonModel,'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve,'DividendValue',DividendYield)
NIPricer =
NumericalIntegration with properties:
Model: [1×1 finmodel.Heston]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 80
DividendType: "continuous"
DividendValue: 0.0200
AbsTol: 1.0000e-10
RelTol: 1.0000e-10
IntegrationRange: [1.0000e-09 Inf]
CharacteristicFcn: @characteristicFcnHeston
Framework: "heston1993"
VolRiskPremium: 0
LittleTrap: 1
FFTPricer = finpricer("FFT",'Model',HestonModel, ... 'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve, ... 'DividendValue',DividendYield,'NumFFT',8192)
FFTPricer =
FFT with properties:
Model: [1×1 finmodel.Heston]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 80
DividendType: "continuous"
DividendValue: 0.0200
NumFFT: 8192
CharacteristicFcnStep: 0.0100
LogStrikeStep: 0.0767
CharacteristicFcn: @characteristicFcnHeston
DampingFactor: 1.5000
Quadrature: "simpson"
VolRiskPremium: 0
LittleTrap: 1
FDPricer = finpricer("FiniteDifference",'Model',HestonModel,'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve,'DividendValue',DividendYield)
FDPricer =
FiniteDifference with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.Heston]
SpotPrice: 80
GridProperties: [1×1 struct]
DividendType: "continuous"
DividendValue: 0.0200
Price Vanilla Instrument
Use the following sensitivities when pricing the Vanilla instrument.
InpSensitivity = ["delta", "gamma", "theta", "rho", "vega", "vegalt"];
Use price to compute the price and sensitivities for the Vanilla instrument that uses the NumericalIntegration pricer.
[PriceNI, outPR_NI] = price(NIPricer,VanillaOpt,InpSensitivity)
PriceNI = 4.7007
outPR_NI =
priceresult with properties:
Results: [1×7 table]
PricerData: []
Use price to compute the price and sensitivities for the Vanilla instrument that uses the FFT pricer.
[PriceFFT, outPR_FFT] = price(FFTPricer,VanillaOpt,InpSensitivity)
PriceFFT = 4.7007
outPR_FFT =
priceresult with properties:
Results: [1×7 table]
PricerData: []
Use price to compute the price and sensitivities for the Vanilla instrument that uses the FiniteDifference pricer.
[PriceFD, outPR_FD] = price(FDPricer,VanillaOpt,InpSensitivity)
PriceFD = 4.7003
outPR_FD =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
Aggregate the price results.
[outPR_NI.Results;outPR_FFT.Results;outPR_FD.Results]
ans=3×7 table
Price Delta Gamma Theta Rho Vega VegaLT
______ _______ ________ _______ ______ ______ ______
4.7007 0.57747 0.03392 -4.8474 20.805 17.028 5.2394
4.7007 0.57747 0.03392 -4.8474 20.805 17.028 5.2394
4.7003 0.57722 0.035254 -4.8483 20.801 17.046 5.2422
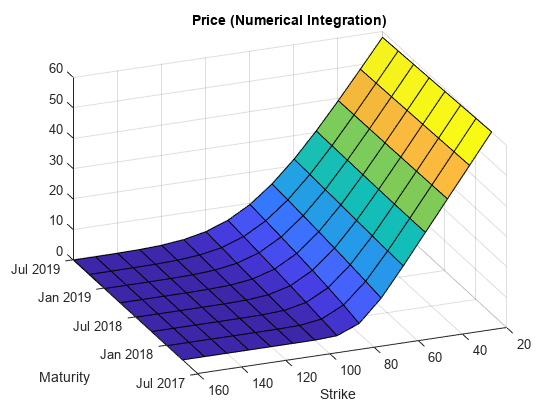
Compute Option Price Surfaces
Use the price function for the NumericalIntegration pricer and the price function for the FFT pricer to compute the prices for a range of Vanilla instruments.
Maturities = datemnth(Settle,(3:3:24)'); NumMaturities = length(Maturities); Strikes = (20:10:160)'; NumStrikes = length(Strikes); [Maturities_Full,Strikes_Full] = meshgrid(Maturities,Strikes); NumInst = numel(Strikes_Full); VanillaOptions(NumInst, 1) = fininstrument("vanilla", ... "ExerciseDate", Maturities_Full(1), "Strike", Strikes_Full(1)); for instidx=1:NumInst VanillaOptions(instidx) = fininstrument("vanilla", ... "ExerciseDate", Maturities_Full(instidx), "Strike", Strikes_Full(instidx)); end Prices_NI = price(NIPricer, VanillaOptions); Prices_FFT = price(FFTPricer, VanillaOptions); figure; surf(Maturities_Full,Strikes_Full,reshape(Prices_NI,[NumStrikes,NumMaturities])); title('Price (Numerical Integration)'); view(-112,34); xlabel('Maturity') ylabel('Strike')
figure; surf(Maturities_Full,Strikes_Full,reshape(Prices_FFT,[NumStrikes,NumMaturities])); title('Price (FFT)'); view(-112,34); xlabel('Maturity') ylabel('Strike')

Since R2024a
This example shows the workflow to price a Vanilla instrument when you use a RoughBergomi model and a RoughVolMonteCarlo pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2019,1,30),'Strike',105,'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 30-Jan-2019
Strike: 105
Name: "vanilla_option"
Create RoughBergomi Model Object
Use finmodel to create a RoughBergomi model object.
RoughBergomiModel = finmodel("RoughBergomi",Alpha=-0.032,Xi=0.1,Eta=0.003,RhoSV=0.9)RoughBergomiModel =
RoughBergomi with properties:
Alpha: -0.0320
Xi: 0.1000
Eta: 0.0030
RhoSV: 0.9000
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create RoughVolMonteCarlo Pricer Object
Use finpricer to create an RoughVolMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("RoughVolMonteCarlo",DiscountCurve=myRC,Model=RoughBergomiModel,SpotPrice=100,SimulationDates=datetime(2019,1,30))outPricer =
RoughBergomiMonteCarlo with properties:
DiscountCurve: [1×1 ratecurve]
SpotPrice: 100
SimulationDates: 30-Jan-2019
NumTrials: 1000
RandomNumbers: []
Model: [1×1 finmodel.RoughBergomi]
DividendType: "continuous"
DividendValue: 0
MonteCarloMethod: "standard"
BrownianMotionMethod: "standard"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,"all")Price = 7.7862
outPR =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×7 table
Price Delta Gamma Lambda Rho Theta Vega
______ _______ ________ ______ ______ ______ ______
7.7862 0.50369 0.012632 6.469 15.947 1.0273 30.741
Since R2024b
This example shows the workflow to price a Vanilla instrument when you use a RoughHeston model and a RoughVolMonteCarlo pricing method.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2019,1,30),'Strike',105,'ExerciseStyle',"european",'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 30-Jan-2019
Strike: 105
Name: "vanilla_option"
Create RoughHeston Model Object
Use finmodel to create a RoughHeston model object.
RoughBergomiModel = finmodel("RoughHeston",V0=0.4,ThetaV=0.3,Kappa=0.2,SigmaV=0.1,Alpha=-0.02,RhoSV=0.3)RoughBergomiModel =
RoughHeston with properties:
Alpha: -0.0200
V0: 0.4000
ThetaV: 0.3000
Kappa: 0.2000
SigmaV: 0.1000
RhoSV: 0.3000
Create ratecurve Object
Create a flat ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Maturity = datetime(2023,9,15); Rate = 0.035; myRC = ratecurve('zero',Settle,Maturity,Rate,'Basis',12)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 12
Dates: 15-Sep-2023
Rates: 0.0350
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create RoughVolMonteCarlo Pricer Object
Use finpricer to create an RoughVolMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value argument.
outPricer = finpricer("RoughVolMonteCarlo",DiscountCurve=myRC,Model=RoughBergomiModel,SpotPrice=100,SimulationDates=datetime(2019,1,30))outPricer =
RoughHestonMonteCarlo with properties:
DiscountCurve: [1×1 ratecurve]
SpotPrice: 100
SimulationDates: 30-Jan-2019
NumTrials: 1000
RandomNumbers: []
Model: [1×1 finmodel.RoughHeston]
DividendType: "continuous"
DividendValue: 0
MonteCarloMethod: "standard"
BrownianMotionMethod: "standard"
Price Vanilla Instrument
Use price to compute the price and sensitivities for the Vanilla instrument.
[Price, outPR] = price(outPricer,VanillaOpt,"all")Price = 13.9392
outPR =
priceresult with properties:
Results: [1×8 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×8 table
Price Delta Gamma Lambda Rho Theta Vega VegaLT
______ _______ ________ ______ ______ _______ ______ ______
13.939 0.54193 0.011253 3.8878 15.143 -22.098 24.539 0
More About
A vanilla option is a category of options that includes only the most standard components.
A vanilla option is based on an underlying asset, which can include stocks, bonds, commodities, currencies, or market indices. The value of the option is derived from the price movement of the underlying asset.
Vanilla options come in two forms: call options and put options. A call option gives the holder the right to buy the underlying asset at the strike price, while a put option gives the holder the right to sell the underlying asset at the strike price. The buyer of a vanilla option pays a premium to the seller or writer of the option in exchange for the rights provided by the option contract. The premium represents the cost of acquiring the option and is influenced by factors such as the price of the underlying asset, time to expiration, volatility, and prevailing market conditions.
The strike price, also known as the exercise price, is the predetermined price at which the underlying asset can be bought (in the case of a call option) or sold (in the case of a put option) if the option is exercised.
A vanilla option has an expiration date and straightforward strike price. After the expiration date, the option becomes void. American-style options and European-style options are both categorized as vanilla options.
The payoff for a vanilla option is as follows:
For a call:
For a put:
where:
St is the price of the underlying asset at time t.
K is the strike price.
For more information, see Vanilla Option.
Tips
After creating a Vanilla instrument object, you can use setExercisePolicy to
change the size of the options. For example, if you have the following
instrument:
VanillaOpt = fininstrument("Vanilla",'ExerciseDate',datetime(2021,5,1),'Strike',29,'OptionType',"put",'ExerciseStyle',"European")Vanilla instrument's size by changing the
ExerciseStyle from "European" to
"American", use setExercisePolicy:VanillaOpt = setExercisePolicy(VanillaOpt,[datetime(2021,1,1) datetime(2022,1,1)],100,'American')
Version History
Introduced in R2020aThe Vanilla instrument object supports pricing with a RoughHeston model and
a RoughVolMonteCarlo pricing method.
The Vanilla instrument object supports pricing with a RoughBergomi model
and a RoughVolMonteCarlo pricing method.
Although Vanilla supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
See Also
Functions
Topics
- Price European Vanilla Call Options Using Black-Scholes Model and Different Equity Pricers
- Use Black-Scholes Model to Price Asian Options with Several Equity Pricers
- Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments
- Choose Instruments, Models, and Pricers
- Supported Exercise Styles
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)