Use Black-Scholes Model to Price Asian Options with Several Equity Pricers
This example shows how to compare arithmetic and geometric Asian option prices using the BlackScholes model and various pricing methods. The pricing methods are: the Kemna-Vorst, Levy, Turnbull-Wakeman, and Cox-Ross-Rubinstein methods and Monte Carlo simulation. This example also demonstrates how variations in spot prices affect option and delta sensitivity values on European vanilla and Asian options.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2019,01,01); Maturity = datetime(2025,01,01); Rate = 0.035; Compounding = -1; Basis = 1; ZeroCurve = ratecurve('zero',Settle,Maturity,Rate,'Compounding',Compounding,'Basis', Basis)
ZeroCurve =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 1
Dates: 01-Jan-2025
Rates: 0.0350
Settle: 01-Jan-2019
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create BlackScholes Model Object
Use finmodel to create a BlackScholes model object.
Volatility = .20; BSModel = finmodel("BlackScholes",'Volatility',Volatility)
BSModel =
BlackScholes with properties:
Volatility: 0.2000
Correlation: 1
Create Asian Instrument Objects
Use fininstrument to create two Asian instrument objects, one using an arithmetic average and the other using a geometric average.
ExerciseDates = datetime(2020,01,01); Strike = 90; OptionType = 'call'; AverageType = 'geometric'; AsianOptArith = fininstrument("Asian",'ExerciseDate',ExerciseDates,'Strike',Strike, ... 'OptionType',OptionType,'Name',"CallAsianArith")
AsianOptArith =
Asian with properties:
OptionType: "call"
Strike: 90
AverageType: "arithmetic"
AveragePrice: 0
AverageStartDate: NaT
ExerciseStyle: "european"
ExerciseDate: 01-Jan-2020
Name: "CallAsianArith"
AsianOptGeo = fininstrument("Asian",'ExerciseDate',ExerciseDates,'Strike',Strike, ... 'OptionType',OptionType,'AverageType', AverageType,'Name',"CallAsianGeo")
AsianOptGeo =
Asian with properties:
OptionType: "call"
Strike: 90
AverageType: "geometric"
AveragePrice: 0
AverageStartDate: NaT
ExerciseStyle: "european"
ExerciseDate: 01-Jan-2020
Name: "CallAsianGeo"
Create Analytic, AssetTree, and AssetMonteCarlo Pricer Objects
Use finpricer to create BlackScholes, AssetTree, and AssetMonteCarlo pricer objects and use the ratecurve object for the 'DiscountCurve' name-value argument.
SpotPrice = 100; InpSensitivity = "delta"; % Analytic Pricers LevyPricer = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', SpotPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "Levy"); TWPricer = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', SpotPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "TurnbullWakeman"); KVPricer = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', SpotPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "KemnaVorst"); % AssetTree Pricer % Define the number of levels of the tree. NumPeriods = 50; CRRPricer = finpricer("AssetTree",'DiscountCurve',ZeroCurve,'Model',BSModel, 'SpotPrice',SpotPrice, ... 'PricingMethod',"CoxRossRubinstein",'NumPeriods', NumPeriods,... 'Maturity', ExerciseDates); % AssetMonteCarlo Pricer % Define the number of simulation trials. NumTrials = 2000; SimDates =[Settle:days(2):ExerciseDates ExerciseDates]; MCPricer = finpricer("AssetMonteCarlo", 'Model', BSModel, 'SpotPrice', SpotPrice, 'DiscountCurve', ZeroCurve, ... 'SimulationDates', SimDates, 'NumTrials', NumTrials);
Calculate the Price of the Arithmetic and Geometric Asian Options Using Different Pricers
Calculate the Asian option prices using the price function for the Analytic, AssetTree, and AssetMonetCarlo pricing methods.
% Analytic [LevyPrice,LevyoutPR] = price(LevyPricer, AsianOptArith,InpSensitivity); [TWPrice, TWoutPR] = price(TWPricer, AsianOptArith, InpSensitivity); [KVPrice, KVoutPR] = price(KVPricer, AsianOptGeo, InpSensitivity); % Cox-Ross-Rubinstein [CRRArithPrice, CRRArithoutPR] = price(CRRPricer, AsianOptArith, InpSensitivity); [CRRGeoPrice, CRRGeooutPR] = price(CRRPricer, AsianOptGeo, InpSensitivity); % Monte Carlo [MCArithPrice, MCArithoutPR] = price(MCPricer, AsianOptArith, InpSensitivity); [MCGeoPrice, MCGeooutPR] = price(MCPricer, AsianOptGeo, InpSensitivity);
Compare Asian Option Prices
Compare the Asian option call prices using the displayPricesAsianCallOption function defined in Local Functions.
displayPricesAsianCallOption(KVPrice,LevyPrice,TWPrice,CRRArithPrice,CRRGeoPrice,MCArithPrice,MCGeoPrice)
Comparison of Asian prices: Arithmetic Asian Levy: 12.164734 Turnbull-Wakeman: 12.164734 Cox-Ross-Rubinstein: 12.126509 Monte Carlo: 12.102669 Geometric Asian Kemna-Vorst: 11.862580 Cox-Ross-Rubinstein: 11.852462 Monte Carlo: 11.988051
The table contrasts the results from closed approximation models against price simulations implemented using the Cox-Ross-Rubinstein binomial tree and Monte Carlo pricing methods. Observe that arithmetic average Asian options are more expensive than their geometric average counterparts.
Compare Asian and Vanilla Options
Asian options are popular instruments since they tend to be less expensive than comparable vanilla calls and puts. This is because the volatility in the average value of an underlier tends to be lower than the volatility of the value of the underlier itself. You can compare the price and delta sensitivity values of Asian options against their vanilla counterparts.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object with same Maturity and Strike as the two Asian options.
EuropeanCallOption = fininstrument("Vanilla",'ExerciseDate',ExerciseDates,'Strike',Strike, ... 'OptionType',OptionType,'Name',"CallVanilla")
EuropeanCallOption =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 01-Jan-2020
Strike: 90
Name: "CallVanilla"
Create Analytic Pricer Object
Use finpricer to create a BlackScholes pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
BLSPricer = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', SpotPrice, 'DiscountCurve', ZeroCurve)
BLSPricer =
BlackScholes with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.BlackScholes]
SpotPrice: 100
DividendValue: 0
DividendType: "continuous"
Compute price and delta sensitivity.
[BLSPrice, BLSoutPR] = price(BLSPricer, EuropeanCallOption, InpSensitivity);
Compare Prices for Asian and Vanilla Options
Compare option prices using the displayVanillaAsianComparison function defined in Local Functions.
displayVanillaAsianComparison('Prices', BLSPrice, KVPrice,LevyPrice,TWPrice)Comparison of Vanilla and Asian Option Prices: Vanilla BLS: 15.743809 Asian Kemna-Vorst: 11.862580 Asian Levy: 12.164734 Asian Turnbull-Wakeman: 12.164734
Observe that both the geometric and arithmetic Asian option prices are lower than their vanilla counterparts.
Compare Delta Sensitivity for Asian and Vanilla Options
The delta value measures the option price sensitivity to changes in the price of the underlying asset. As the underlier changes, the proportions of the instruments forming the portfolio might need to be adjusted to keep the sensitivities within the desired range.
displayVanillaAsianComparison('Delta', BLSoutPR.Results.Delta, KVoutPR.Results.Delta, LevyoutPR.Results.Delta,TWoutPR.Results.Delta)Comparison of Vanilla and Asian Option Delta: Vanilla BLS: 0.788666 Asian Kemna-Vorst: 0.844986 Asian Levy: 0.852806 Asian Turnbull-Wakeman: 0.852806
The table shows the delta values for both the vanilla and arithmetic and geometric Asian options. Observe that the geometric Asian delta value is lower than the delta value for the arithmetic Asian option.
Analyze Effect of Variations of Underlying Asset on Option Prices
Examine the effect of changes of underlying asset prices. Create a plot to show the effect of variations in the price of the underlying asset on the vanilla and Asian option prices.
StockPrices = (50:5:120)'; PriceBLS = nan(size(StockPrices)); PriceKV = PriceBLS; PriceLevy = PriceBLS; PriceTW = PriceBLS; DeltaBLS = PriceBLS; DeltaLevy = PriceBLS; DeltaTW = PriceBLS; DeltaKV = PriceBLS; InpSensitivity = "delta"; idx = 1; for AssetPrice = StockPrices' PricerBLS = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', AssetPrice, ... 'DiscountCurve', ZeroCurve); [PriceBLS(idx), outPRBLS] = price(PricerBLS, EuropeanCallOption, InpSensitivity); DeltaBLS(idx) = outPRBLS.Results.Delta; PricerLevy = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', AssetPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "Levy"); [PriceLevy(idx), outPRLevy] = price(PricerLevy, AsianOptArith, InpSensitivity); DeltaLevy(idx) = outPRLevy.Results.Delta; PricerTW = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', AssetPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "TurnbullWakeman"); [PriceTW(idx), outPRBTW] = price(PricerTW, AsianOptArith, InpSensitivity); DeltaTW(idx) = outPRBTW.Results.Delta; PricerKV = finpricer('Analytic', 'Model', BSModel, 'SpotPrice', AssetPrice, ... 'DiscountCurve', ZeroCurve, 'PricingMethod', "KemnaVorst"); [PriceKV(idx), outPRKV] = price(PricerKV, AsianOptGeo, InpSensitivity); DeltaKV(idx) = outPRKV.Results.Delta; idx = idx+1; end figure('menubar', 'none', 'numbertitle', 'off') plot(StockPrices, [PriceBLS PriceKV PriceLevy PriceTW]); xlabel 'Spot Price ($)' ylabel 'Option Price ($)' title 'Asian and Vanilla Option Price Comparison' legend('Vanilla', 'KV Geometric Asian', 'Levy Arithmetic Asian', 'TW Arithmetic Asian', 'location','northwest');
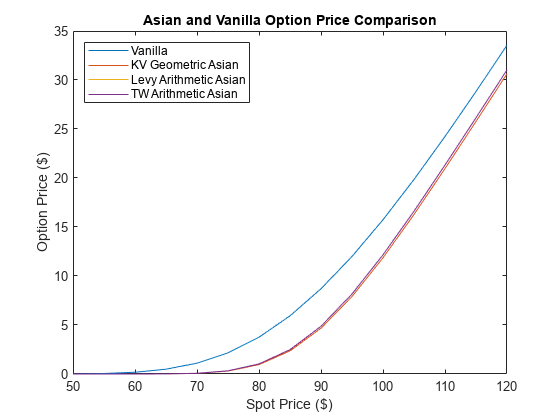
The plot displays vanilla and Asian option prices with respect to the underlying asset price. Observe that the price of the Asian options is cheaper than the price of the vanilla option.
Analyze Effect of Variations of the Underlying Asset on the Options Delta
Examine the effect of changes of underlying asset prices on delta sensitivity. The following plot demonstrates the behavior of the delta value for the Vanilla and Asian options as a function of the underlying price.
figure('menubar', 'none', 'numbertitle', 'off') plot(StockPrices, [DeltaBLS DeltaKV DeltaLevy DeltaTW]); xlabel 'Spot Price ($)' ylabel 'Call Delta' title 'Asian and Vanilla Option Delta Comparison (Strike Price = $90)' legend('Vanilla', 'KV Geometric Asian', 'Levy Arithmetic Asian', 'TW Arithmetic Asian', 'location', 'northwest');

The plot displays the vanilla and Asian delta sensitivity values with respect to the underlying asset price. A vanilla or Asian in-the-money (ITM) call option is more sensitive to price movements than an out-of-the-money (OTM) option. If the asset price is deep in the money, then it is more likely to be exercised. The opposite is the case for an out-of-the-money option. Observe that the Asian delta value is lower for out-of-the-money options and higher for in-the-money options compared with the vanilla European counterpart.
Local Functions
function displayPricesAsianCallOption(KVPrice,LevyPrice,TWPrice,CRRArithPrice,CRRGeoPrice,MCArithPrice,MCGeoPrice) fprintf('Comparison of Asian prices:\n'); fprintf('\n'); fprintf('Arithmetic Asian\n'); fprintf('Levy: %f\n', LevyPrice); fprintf('Turnbull-Wakeman: %f\n', TWPrice); fprintf('Cox-Ross-Rubinstein: %f\n', CRRArithPrice); fprintf('Monte Carlo: %f\n', MCArithPrice); fprintf('\n'); fprintf('Geometric Asian\n'); fprintf('Kemna-Vorst: %f\n', KVPrice); fprintf('Cox-Ross-Rubinstein: %f\n', CRRGeoPrice); fprintf('Monte Carlo: %f\n', MCGeoPrice); end function displayVanillaAsianComparison(type, BLS, KV, Levy, TW) fprintf('Comparison of Vanilla and Asian Option %s:\n', type); fprintf('\n'); fprintf('Vanilla BLS: %f\n', BLS); fprintf('Asian Kemna-Vorst: %f\n', KV); fprintf('Asian Levy: %f\n', Levy); fprintf('Asian Turnbull-Wakeman: %f\n', TW); end
See Also
Topics
- Pricing Asian Options
- Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments
- Choose Instruments, Models, and Pricers
- Supported Exercise Styles