filter
Forward recursion of Bayesian nonlinear non-Gaussian state-space model
Since R2023b
Syntax
Description
filter estimates state-distribution moments of a
Bayesian nonlinear non-Gaussian state-space model (bnlssm), conditioned on model
parameters Θ, for each period of the specified response data by using importance sampling and
resampling in the sequential Monte Carlo (SMC) framework. filter
approximates the state filtering distribution and likelihood function by applying
particles, or weighted random samples.
[
returns approximate state-distribution means X,logL] = filter(Mdl,Y,params)X for each sampling time in
the input response data Y and the corresponding loglikelihood
logL resulting from performing forward recursion of, or filtering, the
Bayesian nonlinear state-space model Mdl.
filter evaluates the parameter map
Mdl.ParamMap by using the vector of parameter values
params.
filter filters Y and particles, weighted
random samples representing state values, through the model by using SMC.
[
additionally returns the following quantities using any of the input-argument combinations
in the previous syntaxes:X,logL,Output,RND] = filter(___)
Output— Filtering results by sampling periodApproximate loglikelihood values associated with the input data, input parameters, and particles
Filter estimate of state-distribution means
Filter estimate of state-distribution covariance
Custom statistics
Effective sample size
Flags indicating which data the software used to filter
Flags indicating resampling
RND— Normal random variables generated byfilterused to reproduce results or reuse random variates generated by a previous call offilter
Examples
This example uses simulated data to compute filter estimates of state distribution means of the following Bayesian nonlinear state-space model in equation. The state-space model contains two independent, stationary, autoregressive states each with a model constant. The observations are a nonlinear function of the states with Gaussian noise. The prior distribution of the parameters is flat. Symbolically, the system of equations is
and are the unconditional means of the corresponding states. The initial distribution moments of each state are their unconditional mean and covariance.
Create a Bayesian nonlinear state-space model characterized by the system. The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series is additive, linear, and Gaussian. The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function and the prior distribution of the parameters. You can use the functions only within this script.
Mdl = bnlssm(@paramMap,@priorDistribution)
Mdl =
bnlssm with properties:
ParamMap: @paramMap
ParamDistribution: @priorDistribution
ObservationForm: "equation"
Multipoint: [1×0 string]
Mdl is a bnlssm model specifying the state-space model structure and prior distribution of the state-space model parameters. Because Mdl contains unknown values, it serves as a template for posterior analysis with observations.
Simulate a series of 100 observations from the following stationary 2-D VAR process.
where the disturbance series are standard Gaussian random variables.
rng(1,"twister") % For reproducibility T = 100; thetatrue = [0.9; 1; -0.75; -1; 0.3; 0.2; 0.1]; MdlSim = varm(AR={diag(thetatrue([1 3]))},Covariance=diag(thetatrue(5:6).^2), ... Constant=thetatrue([2 4])); XSim = simulate(MdlSim,T);
Compose simulated observations using the following equation.
where the innovation series is a standard Gaussian random variable.
ysim = log(sum(exp(XSim - mean(XSim)),2)) + thetatrue(7)*randn(T,1);
To compute state estimates, the filter function requires response data and a model with known state-space model parameters. Choose a random set with the following constraints:
and are within the unit circle. Use to generate values.
and are real numbers. Use the distribution to generate values.
, , and are positive real numbers. Use the distribution to generate values.
theta13 = (-1+(1-(-1)).*rand(2,1)); theta24 = 3*randn(2,1); theta567 = chi2rnd(1,3,1); theta = [theta13(1); theta24(1); theta13(2); theta24(2); theta567];
Compute filtered state estimates and corresponding loglikelihood by passing the Bayesian nonlinear model, simulated data, and parameter values to filter.
[FilterX,logL] = filter(Mdl,ysim,theta); size(FilterX)
ans = 1×2
100 4
logL
logL = -134.1053
FilterX is a 100-by-4 matrix of filter state estimates, with rows corresponding to periods in the sample and columns corresponding to the state variables. logL is the approximate loglikelihood function estimate evaluated at the data and parameter values.
Compare the loglikelihood logL and the loglikelihood computed using from the data simulation.
[FilterXSim,logLSim] = filter(Mdl,ysim,thetatrue); logLSim
logLSim = -0.4078
logLSim > logL, suggesting that the model evaluated at thetaSim has the better fit.
Plot the two sets of filter state estimates with the true state values.
figure tiledlayout(2,1) nexttile plot([FilterX(:,1) FilterXSim(:,1) XSim(:,1)]) title("x_{t,1}") legend("Filter State, random \theta","Filter State, true \theta","XSim") nexttile plot([FilterX(:,3) FilterXSim(:,3) XSim(:,2)]) title("x_{t,3}") legend("Filter State, random \theta","Filter State, true \theta","XSim")

The filter state estimates using the true value of and the simulated state paths are close. The filter state estimates are far from the simulated state paths.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = @(x)blkdiag([theta(1) theta(2); 0 1],[theta(3) theta(4); 0 1])*x; B = [theta(5) 0; 0 0; 0 theta(6); 0 0]; C = @(x)log(exp(x(1)-theta(2)/(1-theta(1))) + ... exp(x(3)-theta(4)/(1-theta(3)))); D = theta(7); Mean0 = [theta(2)/(1-theta(1)); 1; theta(4)/(1-theta(3)); 1]; Cov0 = diag([theta(5)^2/(1-theta(1)^2) 0 theta(6)^2/(1-theta(3)^2) 0]); StateType = [0; 1; 0; 1]; % Stationary state and constant 1 processes end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta([1 3])) >= 1) (theta(5:7) <= 0)]; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
This example shows how to use filter and Bayesian optimization to calibrate a Bayesian nonlinear state-space. Consider this nonlinear state-space model.
where has a flat prior and the series and are standard Gaussian random variables.
Simulate Series
Simulate a series of 100 observations from the following stationary 2-D VAR process.
where the series and are standard Gaussian random variables.
rng(10,"twister") % For reproducibility T = 100; thetaDGP = [0.5; 0.6; -1; 2; 0.75]; numparams = numel(thetaDGP); MdlSim = arima(AR=thetaDGP(1),Variance=sqrt(thetaDGP(2)), ... Constant=0); xsim = simulate(MdlSim,T); ysim = exp(thetaDGP(3).*xsim) + thetaDGP(4) + thetaDGP(5)*randn(T,1);
Create Bayesian Nonlinear Model
Create a Bayesian nonlinear state-space model. The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function and the prior distribution of the parameters. You can use the functions only within this script. Specify Multipoint=["A" "C"] because the state-transition and measurement-sensitivity parameter mappings in paraMap can evaluate multiple particles simultaneously.
Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint=["A" "C"]);
Perform Random Exploration
One way to explore the parameter space for the point that maximizes the likelihood is by random exploration:
Randomly generated set of parameters.
Compute the loglikelihood for that set.
Repeat steps 1 and 2 many times.
Choose the set of parameters that yields the largest loglikelihood.
Perform random exploration for 500 epochs. Choose a random set using the following arbitrary recipe:
.
and are .
and are.
numepochs = 500; numparticles = 10000; theta = NaN(numparams,numepochs); logL = NaN(numepochs,1); for j = 1:numepochs theta(:,j) = [(-1+(1-(-1)).*rand(1,1)); chi2rnd(1,1,1); ... 2*randn(2,1); chi2rnd(1,1,1);]; [~,logL(j)] = filter(Mdl,ysim,theta(:,j),NumParticles=numparticles); end
Choose the set of parameters that maximizes the loglikelihood.
[bestlogL,idx] = max(logL); bestTheta = theta(:,idx); [bestTheta thetaDGP]
ans = 5×2
0.4934 0.5000
0.4843 0.6000
-1.4906 -1.0000
1.6399 2.0000
0.7260 0.7500
The values that maximize the likelihood are fairly close to the values that generated the data.
Perform Bayesian Optimization
Bayesian optimization requires you to specify which variables require optimization and their support. To do this, use optimizableVariable to provide a name to the variable and its support. This example limits the support of each variable to a small interval; you must experiment with the support for your application.
thetaOp(5) = optimizableVariable("theta5",[0,2]); thetaOp(1) = optimizableVariable("theta1",[0,0.9]); thetaOp(2) = optimizableVariable("theta2",[0,2]); thetaOp(3) = optimizableVariable("theta3",[-3,0]); thetaOp(4) = optimizableVariable("theta4",[-3,3]);
thetaOp is an optimizableVariable object specifying the name and support of each variable of .
bayesopt accepts a function handle to the function that you want to minimize with respect to one argument and the optimizable variable specifications. Therefore, provide the function handle neglog, which is associated with the negative loglikelihood function filterneglogl located in Local Functions. Specify the Expected Improvement Plus acquisition function and an exploration ratio of 1.
neglogl = @(var)filterneglogl(var,Mdl,ysim,numparticles); rng(1,"twister") results = bayesopt(neglogl,thetaOp,AcquisitionFunctionName="expected-improvement-plus", ... ExplorationRatio=1);
|==================================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | theta1 | theta2 | theta3 | theta4 | theta5 |
| | result | | runtime | (observed) | (estim.) | | | | | |
|==================================================================================================================================================|
| 1 | Best | 1035.3 | 0.40397 | 1035.3 | 1035.3 | 0.0761 | 0.51116 | -0.78522 | -2.272 | 0.44888 |
| 2 | Best | 331.41 | 0.17732 | 331.41 | 372.47 | 0.5021 | 0.8957 | -0.11662 | -1.1518 | 1.8165 |
| 3 | Best | 249.01 | 0.29428 | 249.01 | 249.04 | 0.67392 | 0.54178 | -2.091 | -0.82814 | 0.63451 |
| 4 | Accept | 381.54 | 0.27129 | 249.01 | 249.17 | 0.74179 | 1.8872 | -1.9159 | -2.5691 | 1.596 |
| 5 | Best | 183.98 | 0.18452 | 183.98 | 184.25 | 0.60884 | 0.17723 | -1.2634 | 2.9947 | 1.8405 |
| 6 | Best | 182.33 | 0.16385 | 182.33 | 183.34 | 0.60034 | 1.5367 | -2.5329 | 2.5026 | 0.91717 |
| 7 | Accept | 247.19 | 0.26901 | 182.33 | 183.13 | 0.89999 | 0.70185 | -1.537 | -1.1312 | 0.7421 |
| 8 | Accept | 274.28 | 0.25769 | 182.33 | 174.46 | 0.59232 | 1.7554 | -1.597 | 0.78832 | 0.13249 |
| 9 | Best | 177.47 | 0.1615 | 177.47 | 177.45 | 0.89577 | 0.097083 | -0.37012 | 2.9984 | 1.5053 |
| 10 | Accept | 1055.7 | 0.26395 | 177.47 | 177.48 | 0.77811 | 1.0092 | -2.4812 | 2.9977 | 0.16125 |
| 11 | Best | 172.82 | 0.35829 | 172.82 | 172.81 | 0.067163 | 0.45713 | -2.0117 | 2.3819 | 1.3694 |
| 12 | Accept | 182.61 | 0.1973 | 172.82 | 172.81 | 0.1524 | 1.3513 | -1.2805 | 1.7846 | 0.96486 |
| 13 | Accept | 293.62 | 0.24223 | 172.82 | 172.8 | 0.020503 | 0.68288 | -0.90552 | -0.39937 | 1.0775 |
| 14 | Accept | 213.33 | 0.13446 | 172.82 | 172.79 | 0.66738 | 1.6267 | -2.0922 | 1.7538 | 1.9997 |
| 15 | Accept | 247.38 | 0.17018 | 172.82 | 172.79 | 0.3893 | 1.9718 | -2.4707 | 1.0908 | 1.5419 |
| 16 | Accept | 221.54 | 0.23971 | 172.82 | 172.78 | 0.72965 | 1.352 | -1.1343 | 0.65708 | 0.6377 |
| 17 | Accept | 188.49 | 0.1662 | 172.82 | 172.88 | 0.89937 | 1.4508 | -2.1551 | 2.0858 | 1.2099 |
| 18 | Accept | 263.15 | 0.25712 | 172.82 | 172.9 | 0.25159 | 1.5215 | -2.4842 | 0.39488 | 1.9982 |
| 19 | Accept | 177.36 | 0.09513 | 172.82 | 172.93 | 0.57453 | 1.14 | -0.67847 | 2.3751 | 1.7098 |
| 20 | Best | 166.08 | 0.11553 | 166.08 | 166.07 | 0.65195 | 0.28152 | -2.3512 | 2.7417 | 1.1739 |
|==================================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | theta1 | theta2 | theta3 | theta4 | theta5 |
| | result | | runtime | (observed) | (estim.) | | | | | |
|==================================================================================================================================================|
| 21 | Accept | 247.18 | 0.15466 | 166.08 | 166.02 | 0.84878 | 1.0539 | -0.32036 | -2.9995 | 1.9983 |
| 22 | Accept | 337.73 | 0.30141 | 166.08 | 166.05 | 0.89869 | 1.5269 | -2.6155 | -0.39382 | 0.97507 |
| 23 | Best | 160.07 | 0.1699 | 160.07 | 159.85 | 0.33986 | 0.23909 | -0.067419 | 2.4482 | 1.0867 |
| 24 | Accept | 173.63 | 0.30559 | 160.07 | 159.86 | 0.00091906 | 1.8085 | -0.45066 | 1.2493 | 0.64013 |
| 25 | Accept | 414.36 | 0.15147 | 160.07 | 159.88 | 0.0704 | 0.13671 | -1.6195 | -2.2701 | 1.9933 |
| 26 | Accept | 333.12 | 0.2776 | 160.07 | 159.87 | 0.021032 | 1.2185 | -2.5641 | -0.33455 | 0.031058 |
| 27 | Accept | 194.78 | 0.2505 | 160.07 | 159.89 | 0.026875 | 0.37482 | -2.8859 | 2.4594 | 1.9964 |
| 28 | Accept | 308.59 | 0.50505 | 160.07 | 160.1 | 0.0012325 | 1.8785 | -1.0062 | -1.135 | 1.1707 |
| 29 | Accept | 187.71 | 0.14556 | 160.07 | 159.92 | 0.052699 | 1.9929 | -0.60616 | 2.7538 | 1.4581 |
| 30 | Accept | 265.81 | 0.20233 | 160.07 | 160.05 | 0.0020435 | 1.6173 | -2.8881 | 1.0742 | 0.92197 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 25.4598 seconds
Total objective function evaluation time: 6.8876
Best observed feasible point:
theta1 theta2 theta3 theta4 theta5
_______ _______ _________ ______ ______
0.33986 0.23909 -0.067419 2.4482 1.0867
Observed objective function value = 160.0736
Estimated objective function value = 160.0527
Function evaluation time = 0.1699
Best estimated feasible point (according to models):
theta1 theta2 theta3 theta4 theta5
_______ _______ _________ ______ ______
0.33986 0.23909 -0.067419 2.4482 1.0867
Estimated objective function value = 160.0527
Estimated function evaluation time = 0.16991

results is a BayesianOptmization object containing properties summarizing the results of Bayesian optimization.
Extract the value that minimizes the negative loglikelihood from results by using bestPoint.
bestPoint(results)
ans=1×5 table
theta1 theta2 theta3 theta4 theta5
_______ _______ _________ ______ ______
0.33986 0.23909 -0.067419 2.4482 1.0867
The results are fairly close to the values that generated the data.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and the log prior distribution of the parameters, and they compute the negative loglikelihood of the model.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = @(x)theta(1)*x; B = theta(2); C = @(x)exp(theta(3).*x) + theta(4); D = theta(5); Mean0 = 0; Cov0 = 1; StateType = 0; % Stationary state process end function logprior = priorDistribution(theta) paramconstraints = [abs(theta(1)) >= 1; theta([2 4]) <= 0]; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end function neglogL = filterneglogl(theta,mdl,resp,np) theta = table2array(theta); [~,logL] = filter(mdl,resp,theta,NumParticles=np); neglogL = -logL; end
When a set of state-space parameters are close in space, they can yield sufficiently different loglikelihood function values. This phenomenon is due to Monte Carlo sampling error. To address Monte Carlo sampling error so that comparisons among of loglikelihoods evaluated from similar parameter values during calibration is more fair, apply Hilbert sorting to the particles. This example reproduces results to show the effects of sorting particles.
Consider this simple linear Gaussian state-space model.
where the error series and are standard Gaussian random variables.
Assuming that the observation innovation variance is 1, simulate a response series of length 300 from the model. The Local Functions section contains the parameter mapping.
T = 300; rng(1,"twister") % For reproducibility MdlTrue = ssm(@paramMap); y = simulate(MdlTrue,T,Params=1);
Specify two values of , at which to evaluate the model, that are close to each other.
theta1 = 0.5; theta2 = 0.5 + 1e-7;
Evaluate the true loglikelihood at each value of by using the filter function of ssm.
[~,logL1] = filter(MdlTrue,y,Params=theta1); [~,logL2] = filter(MdlTrue,y,Params=theta2); [logL1 logL2 abs(logL1-logL2)]
ans = 1×3
-627.5987 -627.5987 0.0000
The values of yield practically identical loglikelihood values.
Create a Bayesian nonlinear state-space model using the parameter mapping and log prior density functions.
Mdl = bnlssm(@paramMap,@priorDistribution);
Evaluate the Bayesian loglikelihood at the values of .
[~,logL1] = filter(Mdl,y,theta1); [~,logL2] = filter(Mdl,y,theta2); [logL1 logL2 abs(logL1-logL2)]
ans = 1×3
-629.1780 -628.4513 0.7267
Despite the arguments being close, there is a difference between their corresponding loglikelihoods. The difference can be attributed to Monte Carlo sampling.
Evaluate the loglikelihood at the value of again using the Bayesian model, but return the normal random variates to reproduce subsequent calls of filter.
[~,logL1,~,rnd] = filter(Mdl,y,theta1); rnd
rnd = struct with fields:
Autocorrelation: 1
Time: 300
Initial: [0×1000 double]
Proposal: {300×1 cell}
Resample: {300×1 cell}
ResampleFlag: [300×1 logical]
rnd is a structure array containing sampling information.
Evaluate the loglikelihood at the value of again, but use the same normal random variates used to evaluate the loglikelihood at .
[~,logL2] = filter(Mdl,y,theta2,RND=rnd); [logL1 logL2 abs(logL1-logL2)]
ans = 1×3
-629.3398 -629.2906 0.0491
Still, the loglikelihoods are different.
Evaluate the loglikelihood at the values of by passing them and normal variates to filter again. Apply Hilbert sorting to the particles.
[~,logL1,~,rnd] = filter(Mdl,y,theta1,SortParticles=true); [~,logL2] = filter(Mdl,y,theta2,RND=rnd,SortParticles=true); [logL1 logL2 abs(logL1-logL2)]
ans = 1×3
-631.4925 -631.4925 0.0000
Although the loglikelihood magnitudes are different from the frequentist state-space model, they are practically the same for values of that are very close to each other.
Local Functions
These functions specify the state-space model parameter mapping, in equation form, and log prior distribution of the parameter.
function [A,B,C,D,mean0,Cov0] = paramMap(theta) A = 1; B = 1; C = 1; D = theta; mean0 = 0; Cov0 = 0; end function logprior = priorDistribution(theta) paramconstraints = theta <= 0; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
This example compares the performance of several SMC proposal particle resampling methods for obtaining filtered state estimates of a quasi-nonnegative constrained state space model, which models nonnegative state quantities such as interest rates and prices:
and are iid standard Gaussian random variables.
Generate Artificial Data
Consider the following data-generating process (DGP)
Generate a random series of 200 observations from the DGP.
a0 = 0.1; a1 = 0.95; b = 1; d = 0.5; theta = [a0; a1; b; d]; T = 50; % Preallocate variables x = zeros(T,1); y = zeros(T,1); rng(0,"twister") % For reproducibility u = randn(T,1); e = randn(T,1); for t = 2:T x(t) = max(0,a0 + a1*x(t-1)) + b*u(t); y(t) = x(t) + d*e(t); end
Create Bayesian Nonlinear State-Space Model
The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function paramMap and the prior distribution of the parameters priorDistribution. You can use the functions only within this script.
The paramMap function has these qualities:
Functions can simultaneously evaluate the state equation for multiple values of
A. Therefore, you can speed up calculations by specifying theMultipoint="A"option.The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series is additive, linear, and Gaussian.
The priorDistribution function specifies a flat prior, which has a density that is proportional to 1 everywhere in the parameter space; it constrains the error standard deviations to be positive.
Create a Bayesian nonlinear state-space model characterized by the system.
Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint="A");Obtain Filtered State Estimates Using Each Proposal Sampler Method
Obtain filtered state estimates using the joint distribution of the parameters, at a randomly drawn set of values in [0,1], using the bootstrap, optimal, and one-pass unscented particle resampling methods. Specify drawing 5000 particles for SMC.
numParticles = 5000; params = rand(4,1); smcMethod = ["bootstrap" "optimal" "unscented"]; for j = 3:-1:1 % Set last element first to preallocate entire cell vector xFilter{j} = filter(Mdl,y,params,NewSamples=smcMethod(j),NumParticles=numParticles); end
Compare the posterior means from each method with the true values.
figure tiledlayout(3,1) for j = 1:3 nexttile plot([x xFilter{j}]) title("SMC Method: " + upper(smcMethod(j))) end legend("True","Filter")
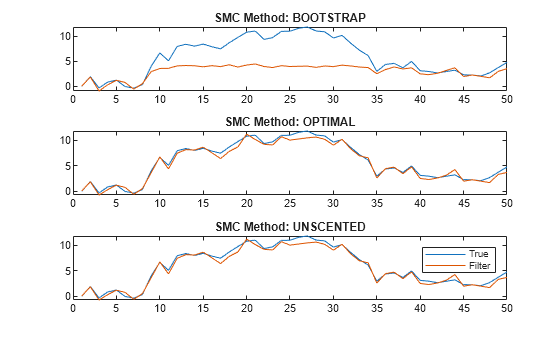
The figure shows that, in this case, the optimal and one-pass unscented methods yield filtered state estimates closer to the true values than the bootstrap method. For the bootstrap method, filtered state estimates in periods 10 through 35 level off around 5, while the true values jump as high as 10. The reason is the bootstrap filter updates particles solely by the transition equation—observations do not inform how particles are updated unlike the optimal and unscented methods.
Regardless of method, filter weighs particles by the observation densities. In this example, the observation equation is (as specified in params). For the bootstrap filter, the normally distributed observation innovation, with small loading 0.17, cannot accommodate large jumps, such as from 5 to 10. Consequently, the weights are degenerate: the largest particle takes all the weight, and filter discards the remaining particles during resampling because they have zero weight. The filtered states level off until period 35 when the observations fall below 5.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.
function [A,B,C,D,mean0,Cov0] = paramMap(params) a0 = params(1); a1 = params(2); b = params(3); d = params(4); A = @(x) max(0,a0+a1.*x); B = b; C = 1; D = d; mean0 = 0; Cov0 = 1; end function logprior = priorDistribution(theta) paramconstraints = theta(3:4) <= 0; % b and d are greater than 0 if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
Input Arguments
Observed response data, specified as a numeric matrix or a cell vector of numeric vectors.
If
Mdlis time invariant with respect to the observation equation,Yis a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row ofYcontains the latest observations.If
Mdlis time varying with respect to the observation equation,Yis a T-by-1 cell vector.Y{t}contains an nt-dimensional vector of observations for period t, where t = 1, ..., T. For linear observation models, the corresponding dimensions of the coefficient matrices, outputs ofMdl.ParamMap,C{t}, andD{t}must be consistent with the matrix inY{t}for all periods. For nonlinear observation models, the dimensions of the inputs and outputs associated with the observations must be consistent. Regardless of model type, the last cell ofYcontains the latest observations.
NaN elements indicate missing observations. For details on how
filter accommodates missing observations, see Algorithms.
Data Types: double | cell
State-space model parameters Θ to evaluate the parameter mapping
Mdl.ParamMap, specified as a numparams-by-1
numeric vector. Elements of params must correspond to the elements of
the first input arguments of Mdl.ParamMap and
Mdl.ParamDistribution.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: filter(Mdl,Y,params,NumParticles=1e4,Resample="residual")
specifies 1e4 particles for the SMC routine and to resample
residuals.
Number of particles for SMC, specified as a positive integer.
Example: NumParticles=1e4
Data Types: double
Since R2025a
SMC proposal (importance) distribution, specified as a value in this table.
| Value | SMC Sampler | Description |
|---|---|---|
"bootstrap" | Bootstrap forward filter [7] | SMC samples particles form the state transition distribution (observations do not inform the sampler). This option
is available only for models with observation noise (nonzero
This method has a relatively low computational cost, but it does not inform the routine of the current observations, which can increase the Monte Carlo sampling variance. |
"optimal" | Conditionally optimal proposal [5] | SMC samples particles from the one-step filtering distribution with incremental weights proportional to the likelihood (observations inform the sampler). The weights have minimum variance. This option is available for the following tractable models supplied in equation form:
|
"unscented" | Unscented transformation [9] | SMC proposal distribution is the one-step filtering distribution approximated by the unscented transformation (observations inform the sampler). This option is
available only for models in equation form with observation noise
(nonzero By default, this option
uses the filtered state mean as the representative point, around
which the algorithm generates sigma points. To specify all particles
as representative points for the unscented transformation, set
|
Example: NewSamples="unscented"
Data Types: char | string
Since R2025a
Flag to apply unscented transformation to all particles, specified as a value in this table.
| Value | Description |
|---|---|
false | The filtered state mean is the representative point, around which the algorithm generates sigma points. This
option is less computationally expensive than
|
true | All particles are the representative points. This option is more computationally expensive than the default, but it can yield a higher-quality proposal distribution. |
Example: MultiPassUnscented=false
Data Types: logical
SMC resampling method, specified as a value in this table.
| Value | Description |
|---|---|
"multinomial" | At time t, the set of previously generated particles (parent set) follows a standard multinomial distribution, with probabilities proportional to their weights. An offspring set is resampled with replacement from the parent set [1]. |
"residual" | Residual sampling, a modified version of multinomial resampling that can produce an estimator with lower variance than the multinomial resampling method [8]. |
"systematic" | Systematic sampling, which produces an estimator with lower variance than the multinomial resampling method [3]. |
Resampling methods downsample insignificant particles to achieve a smaller estimator variance than if no resampling is performed and to avoid sampling from a degenerate proposal [6].
Example: Resample="residual"
Data Types: char | string
Effective sample size threshold, below which filter resamples particles, specified as a nonnegative scalar. For more details, see [6], Ch. 12.3.3.
Tip
To resample during every period, set
Cutoff=numparticles, wherenumparticlesis the value of theNumParticlesname-value argument.To avoid resampling, set
Cutoff=0.
Example: Cutoff=0.75*numparticles
Data Types: double
Flag for sorting particles before resampling, specified as a value in this table.
| Value | Description |
|---|---|
true | filter sorts the generated particles before resampling them. |
false | filter does not sort the generated particles. |
When SortPartiles=true, filter uses Hilbert sorting during the SMC routine to sort the particles. This action can reduce Monte Carlo variation, which is useful when you compare loglikelihoods resulting from evaluating several params arguments that are close to each other [4]. However, the sorting routine requires more computation resources, and can slow down computations, particularly in problems with a high-dimensional state variable.
Example: SortParticles=true
Data Types: logical
Custom function of particles and normalized weights for monitoring the SMC, specified as a function handle (@customstats).
The associated function signature must have this form:
function stat = customStatistics(particles,weights)
where:
customStatisticsparticlesis the mt-by-NumParticleschosen particles at forward-filtering time t of the SMC routine.weightsis the 1-by-NumParticlesnormalized importance weights, corresponding toparticles, at forward-filtering time t of the SMC routine.statis the evaluation ofcustomStatisticsatparticlesandweightsat forward-filtering time t of the SMC routine. For example,statcan be a numeric vector or structure array.
Example: You can return the particles and weights at each filtering step by setting CustomStatistics=@customstats, where you write customstats to return those inputs in a structure array: stat.p = particles; stat.w = weights;
Data Types: function_handle
Previously generated normal random numbers to reproduce filter results, specified as the RND output, a structure array, of previous filter call.
The default is an empty structure array, which causes filter to generate new random numbers.
Data Types: struct
Output Arguments
Approximate filtered state estimates E(xt|y1,…,yt), returned as a T-by-m numeric matrix or a T-by-1 cell vector of numeric vectors.
Each row corresponds to a time point in the sample. The last row contains the latest filtered states.
For time-invariant models, filter returns a matrix. Each
column corresponds to a state variable
xt.
If Mdl is time varying, X is a cell vector.
Cell t contains a column vector of filtered state estimates with
length mt. Each column corresponds to a state
variable.
Approximate loglikelihood function value log p(y1,…,yT).
The loglikelihood value has noise induced by SMC.
Missing observations do not contribute to the loglikelihood.
SMC filtering results by period, returned as a structure array.
Output is a T-by-1 structure, where element
t corresponds to the filtering result for time
t.
| Field | Description | Estimate/Approximation of |
|---|---|---|
LogLikelihood | Scalar approximate loglikelihood objective function value | log p(yt|y1,…,yt) |
FilteredStates | mt-by-1 vector of approximate filtered state estimates | |
FilteredStatesCov | mt-by-mt variance-covariance matrix of filtered states | |
CustomStatistics | Determined by CustomStatistics setting | Determined by CustomStatistics setting |
EffectiveSampleSize | Effective sample size for importance sampling, a scalar in
[0,NumParticles] | N/A |
DataUsed | ht-by-1 flag indicating whether
the software filters using a particular observation. For example, if
observation j at time t is a
NaN, element j in
DataUsed at time t is
0. | N/A |
Resampled | Flag indicating whether filter resampled
particles | N/A |
SMC normal random variate information to reproduce results of subsequent calls of
filter, returned as a structure array.
To reproduce subsequent filtering results or to use the same random variates as previously used:
Set a random number seed by using the
rngfunction.Return
RNDwhen you callfilter.Set the
RNDname-value argument to the outputRNDwhen you callfilteragain to reproduce results or reuse the random variates inRND.
Tips
Smoothing has several advantages over filtering.
The smoothed state estimator is more accurate than the online filter state estimator because it is based on the full-sample data, rather than only observations up to the estimated sampling time.
A stable approximation to the gradient of the loglikelihood function, which is important for numerical optimization, is available from the smoothed state samples of the simulation smoother (finite differences of the approximated loglikelihood computed from the filter state estimates is numerically unstable).
You can use the simulation smoother to perform Bayesian estimation of the nonlinear state-space model via the Metropolis-within-Gibbs sampler.
Unless you set
Cutoff=0,filterresamples particles according to the specified resampling methodResample. Although resampling particles with high weights improves the results of the SMC, you should also allow the sampler traverse the proposal distribution to obtain novel, high-weight particles. To do this, experiment withCutoff.Avoid an arbitrary choice of the initial state distribution.
bnlssmfunctions generate the initial particles from the specified initial state distribution, which impacts the performance of the nonlinear filter. If the initial state specification is bad enough, importance weights concentrate on a small number of particles in the first SMC iteration, which might produce unreasonable filtering results. This vulnerability of the nonlinear model behavior contrasts with the stability of the Kalman filter for the linear model, in which the initial state distribution usually has little impact on the filter because the prior is washed out as it processes data.
Algorithms
filter accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.
References
[1] Andrieu, Christophe, Arnaud Doucet, and Roman Holenstein. "Particle Markov Chain Monte Carlo Methods." Journal of the Royal Statistical Society Series B: Statistical Methodology 72 (June 2010): 269–342. https://doi.org/10.1111/j.1467-9868.2009.00736.x.
[2] Andrieu, Christophe, and Gareth O. Roberts. "The Pseudo-Marginal Approach for Efficient Monte Carlo Computations." Ann. Statist. 37 (April 2009): 697–725. https://dx.doi.org/10.1214/07-AOS574.
[3] Carpenter, James, Peter Clifford, and Paul Fearnhead. "Improved Particle Filter for Nonlinear Problems." IEE Proceedings - Radar, Sonar and Navigation 146 (February 1999): 2–7. https://doi.org/10.1049/ip-rsn:19990255.
[4] Deligiannidis, George, Arnaud Doucet, and Michael Pitt. "The Correlated Pseudo-Marginal Method." Journal of the Royal Statistical Society, Series B: Statistical Methodology 80 (June 2018): 839–870. https://doi.org/10.1111/rssb.12280.
[5] Doucet, Arnaud, Simon Godsill, and Christophe Andrieu. "On Sequential Monte Carlo Sampling Methods for Bayesian Filtering." Statistics and Computing 10 (July 2000): 197–208. https://doi.org/10.1023/A:1008935410038.
[6] Durbin, J, and Siem Jan Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.
[7] Gordon, Neil J., David J. Salmond, and Adrian F. M. Smith. "Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation." IEE Proceedings F Radar and Signal Processing 140 (April 1993): 107–113. https://doi.org/10.1049/ip-f-2.1993.0015.
[8] Liu, Jun, and Rong Chen. "Sequential Monte Carlo Methods for Dynamic Systems." Journal of the American Statistical Association 93 (September 1998): 1032–1044. https://dx.doi.org/10.1080/01621459.1998.10473765.
[9] van der Merwe, Rudolph, Arnaud Doucet, Nando de Freitas, and Eric Wan. "The Unscented Particle Filter." Advances in Neural Information Processing Systems 13 (November 2000). https://dl.acm.org/doi/10.5555/3008751.3008833.
Version History
Introduced in R2023bWhile the SMC routine implements forward filtering, it resamples particles to align them to
the target distribution. The NewSamples name-value argument enables you
to choose how the SMC sampler chooses the particles. The supported algorithms are the
bootstrap forward filter ("bootstrap"), the conditionally optimal
proposal ("optimal"), and the unscented transformation
("unscented).
By default, the unscented transformation uses the filtered state mean as the representative
point, around which sigma points are generated. The MultiPassUnscented
name-value argument enables you to specify all particles as representative points for the
unscented transformation.
Before R2025a, the functions implement forward filtering using only the bootstrap filter.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)