dsp.DCBlocker
Block DC component (offset) from input signal
Description
The dsp.DCBlocker
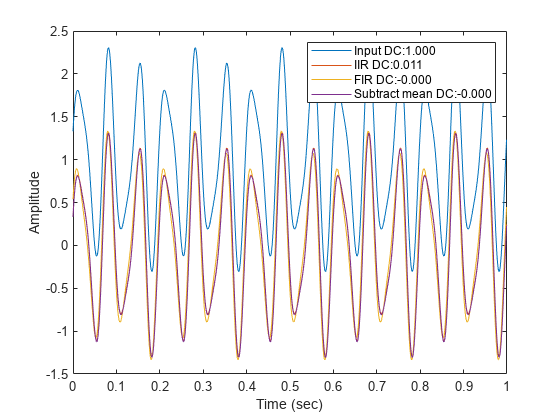
System object™ removes the DC offset from each channel (column) of the input signal. The
operation runs over time to continually estimate and remove the DC offset.
To block the DC component of the input signal:
Create the
dsp.DCBlockerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
The object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.
Creation
Description
dcblker = dsp.DCBlockerdcblker, to block the DC component from each channel
(column) of the input signal.
dcblker = dsp.DCBlocker(Name=Value)NormalizedBandwidth to 0.004.
Properties
Usage
Description
dcblkerOut = dcblker(input)
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Nezami, M. “Performance Assessment of Baseband Algorithms for Direct Conversion Tactical Software Defined Receivers: I/Q Imbalance Correction, Image Rejection, DC Removal, and Channelization.” MILCOM, 2002.