Channelizer
Polyphase FFT analysis filter bank
Libraries:
DSP System Toolbox /
Filtering /
Multirate Filters
Description
The Channelizer block separates a broadband input signal into multiple
narrow subbands using an FFT-based analysis filter bank. The filter bank uses a
prototype lowpass filter and is implemented using a polyphase structure. You can specify
the filter coefficients directly or through design parameters. When you specify the
design parameters, the filter is designed using the designMultirateFIR function.
This block accepts variable-size inputs, so you can change the size of each input channel during simulation. However, the number of channels cannot change.
Examples
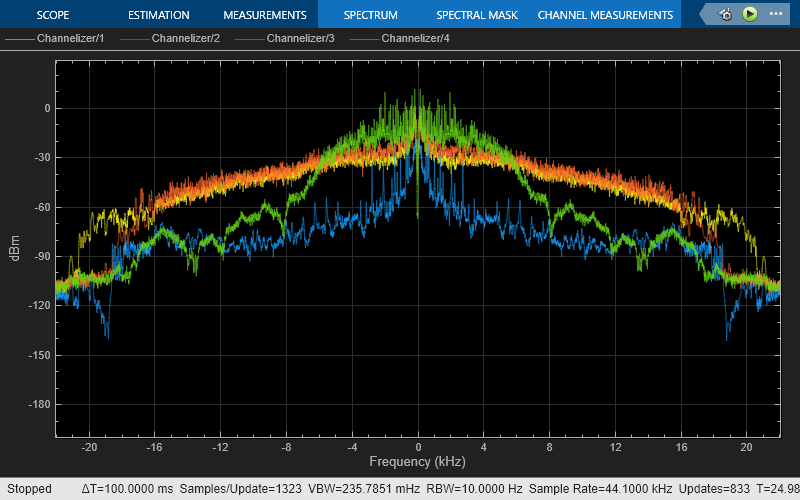
High Resolution Filter-Bank-Based Power Spectrum Estimation
Perform high resolution spectral analysis by using an efficient polyphase filter bank sometimes referred to as a channelizer.
Ports
Input
Specify the input broadband signal that the channelizer splits into multiple narrow bands.
When you input a variable-size signal (frame length changes during simulation), the frame length of the signal can be arbitrary, that is, the input frame length does not have to be a multiple of the decimation factor.
When you input a fixed-size signal (frame length does not change during simulation), the frame length can be arbitrary only when you select the Allow arbitrary frame length for fixed-size input signals parameter.
This port is unnamed until you set Polyphase filter
specification to Coefficients
and select the Specify coefficients from input port
parameter.
Data Types: single | double
Complex Number Support: Yes
Coefficients of the prototype lowpass filter. There must be at least one coefficient per frequency band. If the length of the lowpass filter is less than the number of frequency bands, the block zero-pads the coefficients.
If you specify complex coefficients, the block designs a prototype filter that is centered at a nonzero frequency, also known as a bandpass filter. The modulated versions of the prototype bandpass filter appear with respect to the prototype filter and are wrapped around the frequency range [−Fs Fs].
Dependencies
This port appears when you set Polyphase filter
specification to
Coefficients and select the
Specify coefficients from input port
parameter.
Data Types: single | double
Complex Number Support: Yes
Output
Multiple narrow subbands of the input broadband signal, returned as a vector, matrix, or 3-D array. The number of output ports and the dimension of each port depends on the dimensions of the input signal and whether you select the Bands as separate output ports (Max. of 16 bands) parameter. (since R2024a)
When you select the
Bands as separate output ports (Max. of 16
bands) parameter, the block outputs each narrowband
signal at a separate port. The number of output ports is in the range [1
min(Number of frequency
bands, 16)]. When you clear the Bands as
separate output ports (Max. of 16 bands) parameter, the
block outputs each narrowband signal as a separate column in the output
array and outputs the array at a single output port. (since R2024a)
This table provides more information on the dimensions of the output signal when you input a fixed-size input signal (frame size does not change during simulation).
| Input Signal | Conditions | Output Signal |
|---|---|---|
L-by-1 column vector, where L is a multiple of M and M is the number of frequency bands. You can specify M using the Number of frequency bands parameter. | Clear the Bands as separate output ports (Max. of 16 bands) parameter | (L/M)-by-M |
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M narrowband signals of size (L/M)-by-1 at each of the M output ports. If M > 16, the size of the narrowband signal at the last output port is (L/M)-by-(M−15). | |
L-by-1 column vector, where L is not a multiple of M Select the Allow arbitrary frame length for fixed-size input signals parameter. If you do not select Allow arbitrary frame length for fixed-size input signals, the block errors. | Clear the Bands as separate output ports (Max. of 16 bands) parameter |
|
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M
narrowband signals of size
If M > 16, the
size of the narrowband signal at the last output
port is
| |
L-by-N matrix, where L is a multiple of M | Clear the Bands as separate output ports (Max. of 16 bands) parameter | (L/M)-by-M-by-N |
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M narrowband signals of size (L/M)-by-N at each of the M output ports. If M > 16, the size of the narrowband signal at the last output port is (L/M)-by-(M−15)-by-N. | |
L-by-N matrix, where L is not a multiple of M Select the Allow arbitrary frame length for fixed-size input signals parameter. If you do not select Allow arbitrary frame length for fixed-size input signals, the block errors. | Clear the Bands as separate output ports (Max. of 16 bands) parameter |
|
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M
narrowband signals of size
If M > 16, the
size of the narrowband signal at the last output
port is
|
This table provides more information on the dimensions of the output signal when you input a variable-size input signal (where signal frame size changes during simulation).
| Input Signal | Conditions | Output Signal |
|---|---|---|
L-by-1 column vector, where L is a multiple of M | Clear the Bands as separate output ports (Max. of 16 bands) parameter | (L/M)-by-M |
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M narrowband signals of size (L/M)-by-1 at each of the M output ports. If M > 16, the size of the narrowband signal at the last output port is (L/M)-by-(M−15). | |
L-by-1 column vector, where L is not a multiple of M The block ignores the Allow arbitrary frame length for fixed-size input signals parameter. | Clear the Bands as separate output ports (Max. of 16 bands) parameter |
|
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M
narrowband signals of size
If M > 16, the
size of the narrowband signal at the last output
port is
| |
L-by-N matrix, where L is a multiple of M | Clear the Bands as separate output ports (Max. of 16 bands) parameter | (L/M)-by-M-by-N |
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M narrowband signals of size (L/M)-by-N at each of the M ports. If M > 16, the size of the narrowband signal at the last output port is (L/M)-by-(M−15)-by-N. | |
L-by-N matrix, where L is not a multiple of M The block ignores the Allow arbitrary frame length for fixed-size input signals parameter. | Clear the Bands as separate output ports (Max. of 16 bands) parameter |
|
Select the Bands as separate output ports (Max. of 16 bands) parameter | The block outputs M
narrowband signals of size
If M > 16, the
size of the narrowband signal at the last output
port is
|
Data Types: single | double
Complex Number Support: Yes
Parameters
If a parameter is listed as tunable, then you can change its value during simulation.
Specify the number of frequency bands M into which the block separates the input broadband signal. This parameter indicates the FFT length and the decimation factor used by the algorithm.
Specify the decimation factor D to one of these:
Number of frequency bands–– When you change the value of the Number of frequency bands parameter, the decimation factor changes automatically. (since R2024a)Positive integer less than or equal to the number of frequency bands M.
If the decimation factor D equals the number of frequency bands M, then the M/D ratio equals 1, and the channelizer is known as the maximally decimated channelizer.
If the M/D ratio is greater than
1, the output sample rate is different from the
channel spacing, and the channelizer is known as the non-maximally decimated
channelizer. If the ratio is an integer, the channelizer is known as the
integer-oversampled channelizer. If the ratio is not an integer, say 4/3,
the channelizer is known as the rationally oversampled channelizer. For more
details, see Algorithm.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Number of taps per band and stopband attenuation— Specify the filter design parameters through the Number of filter taps per frequency band and Stopband attenuation (dB) parameters. When you specify the design parameters, the filter is designed using thedesignMultirateFIRfunction.Coefficients— Specify the filter coefficients directly using the Prototype lowpass filter coefficients parameter or input them through the coeffs port.
Number of filter coefficients that each polyphase branch uses. The number of polyphase branches matches the number of frequency bands. The total number of filter coefficients for the prototype lowpass filter is given by Number of frequency bands × Number of filter taps per frequency band. For a given stopband attenuation, increasing the number of taps per band narrows the transition width of the filter. As a result, there is more usable bandwidth for each frequency band, at the expense of increased computation.
Dependencies
To enable this parameter, set Polyphase filter
specification to Number of taps per band and
stopband attenuation.
Stopband attenuation of the lowpass filter, in dB. This value controls the maximum amount of aliasing from one frequency band to the next. As the stopband attenuation increases, the passband ripple decreases.
Dependencies
To enable this parameter, set Polyphase filter
specification to Number of taps per band and
stopband attenuation.
When you select this parameter, the lowpass filter coefficients are input through the coeffs port. When you clear this parameter, the coefficients are specified on the block dialog through the Prototype lowpass filter coefficients parameter.
Dependencies
To enable this parameter, set Polyphase filter
specification to
Coefficients.
Coefficients of the prototype lowpass filter. The default value is the
coefficients vector that rcosdesign(0.25,6,8,'sqrt')
returns. There must be at least one coefficient per frequency band. If the
length of the lowpass filter is less than the number of frequency bands, the
block zero-pads the coefficients.
If you specify complex coefficients, the block designs a prototype filter that is centered at a nonzero frequency, also known as a bandpass filter. The modulated versions of the prototype bandpass filter appear with respect to the prototype filter and are wrapped around the frequency range [−Fs Fs].
Tunable: Yes
Dependencies
To enable this parameter, set Polyphase filter
specification to Coefficients
and clear the Specify coefficients from input port
parameter.
Complex Number Support: Yes
Specify whether fixed-size input signals (whose size does not change during simulation) can have an arbitrary frame length, where the frame length does not have to be a multiple of the decimation factor. The block uses this parameter setting only for fixed-size input signals and ignores this parameter if the input has a variable-size.
When the input signal is a variable-size signal, the signal can have arbitrary frame length, that is, the frame length does not have to be a multiple of the decimation factor.
For fixed-size input signals, if you:
Select the Allow arbitrary frame length for fixed-size input signals parameter, the frame length of the signal does not have to be a multiple of the decimation factor. If the input is not a multiple of the decimation factor, then the output is generally a variable-size signal. Therefore, to support arbitrary input size, the block must also support variable-size operations, which you can enable by selecting the Allow arbitrary frame length for fixed-size input signals parameter.
Clear the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length must be a multiple of the decimation factor.
Since R2024a
When you select this parameter, the block provides a separate output port
for each frequency band. The number of output ports equals
min(Number of frequency bands,
16). The block labels each output port as
Bandx, where
x can be a value in the range [1
min(Number of frequency bands,
16)].
For more information on the signal size on each output port, see the Output(s) port description.
Specify the type of simulation to run. You can set this parameter to:
Interpreted execution–– Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation–– Simulate model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
The generic analysis filter bank consists of a series of parallel bandpass filters that split an input broadband signal, x[n], into a series of narrow subbands. Each bandpass filter retains a different portion of the input signal. After the bandwidth is reduced by one of the bandpass filters, the signal is downsampled to a lower sampling rate commensurate with the new bandwidth.

To implement the analysis filter bank efficiently, the channelizer uses a prototype lowpass filter.
The prototype lowpass filter has an impulse response of h[n], a normalized two-sided bandwidth of 2π/M, and a cutoff frequency of π/M. M is the number of frequency bands, that is, the branches of the analysis filter bank. This value corresponds to the FFT length that the filter bank uses. M can be high on the order of 2048 or more. The stopband attenuation determines the minimum level of interference (aliasing) from one frequency band to another. The passband ripple must be small so that the input signal is not distorted in the passband.
The prototype lowpass filter corresponds to H0(z) in the filter bank. The first branch of the filter bank contains H0(z) followed by the decimator. The other M – 1 branches contain filters that are modulated versions of the prototype filter. The modulation factor is given by the following equation:
The transfer function of the modulated kth bandpass filter is given by:
This figure shows the frequency response of M filters.

To obtain the frequency response characteristics of the filter Hk(z), where k = 1, … , M−1, uniformly shift the frequency response of the prototype filter, H0(z), by multiples of 2π/M. Each subband filter, Hk(z), {k = 1, … , M – 1}, is derived from the prototype filter.
Following is an equivalent representation of the frequency response diagram with ω ranging from [−π π].

The frequency components in the input signal, x[n], are translated in frequency to baseband by multiplying x[n] with the complex exponentials, , where , and . The resulting product signals are passed through the lowpass filters, H0(z). The output of the lowpass filter is relatively narrow in bandwidth. Downsample the signal commensurate with the new bandwidth. Choose a decimation factor, D ≤ M, where M is the number of branches of the analysis filter bank. When D < M, the channelizer is known as oversampled or non-maximally decimated channelizer.
The figure shows an analysis filter bank that uses the prototype lowpass filter.

y1[m], y2[m], … , yM−1[m] are narrow subband signals translated into baseband.
Algorithms
The analysis filter bank can be implemented efficiently using the polyphase structure. For more details on the analysis filter bank, see Analysis Filter Bank.
To derive the polyphase structure, start with the transfer function of the prototype lowpass filter:
N + 1 is the length of the prototype filter.
You can rearrange this equation as follows:
M is the number of polyphase components.
You can write this equation as:
E0(zM), E1(zM), … , EM−1(zM) are polyphase components of the prototype lowpass filter H0(z).
The other filters in the filter bank, Hk(z), where k = 1, … , M−1, are modulated versions of this prototype filter.
You can write the transfer function of the kth modulated bandpass filter as .
Replacing z with ze-jwk and ,
In polyphase form, the equation is as follows:
For all M channels in the filter bank, the transfer function H(z) is given by:
When D = M, the channelizer is known as the maximally decimated channelizer or critically sampled channelizer.
Here is the multirate noble identity for decimation, assuming that D = M.
![]()
For example, consider the first branch of the filter bank that contains the lowpass filter.
![]()
Replace H0(z) with its polyphase representation.

After applying the noble identity for decimation, you can replace the delays and the decimation factor with a commutator switch. The switch starts on the first branch 0 and moves in the counterclockwise direction as shown in the following diagram. The accumulator at the output receives the processed input samples from each branch of the polyphase structure and accumulates these processed samples until the switch goes to branch 0. When the switch goes to branch 0, the accumulator outputs the accumulated value.

For all M channels in the filter bank, the transfer function H(z) is given by:
The matrix on the left is an inverse discrete Fourier transform (IDFT) matrix. With the IDFT matrix, the efficient implementation of the lowpass prototype-based filter bank looks like the following.
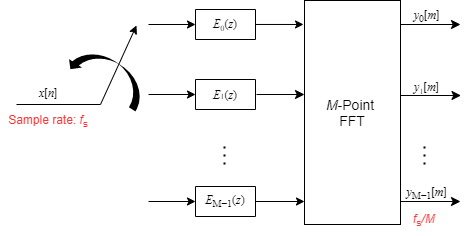
When the channelizer receives the first input sample, the switch feeds this input to the branch 0 and the channelizer computes the first set of output values. As more input samples come in, the switch moves in the counterclockwise direction through branches M−1, M−2, all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as the data keeps coming in. Every time the switch comes to the first branch 0, the channelizer outputs y0[m], y1[m], … , yM-1[m]. Each branch in the channelizer effectively outputs one sample for every M samples it receives. Hence, the sample rate at the output of the channelizer is fs/M.
If you use the M-point FFT, the implementation looks like the following.
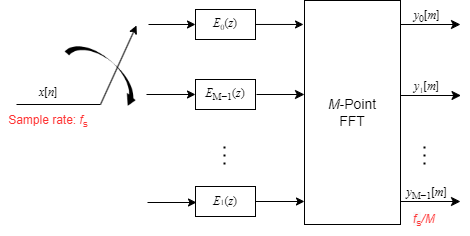
When the switch delivers the first sample to branch 0, the channelizer computes the first set of output values. As more data comes in, the switch moves in the clockwise direction to branches M−1, M−2, all the way up to branch 1, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as more data keeps coming in.
When D < M, the channelizer is known as the non-maximally decimated channelizer or oversampled channelizer. In this configuration, the output sample rate is different from the channel spacing. The non-maximally decimated channelizers offer increased design freedom, but at the expense of increasing computational cost.
If the ratio M/D equals an integer that is greater than 1 and is less than or equal to M−1, the channelizer is known as integer-oversampled channelizer. If the ratio M/D is not an integer, then the channelizer is known as rationally-oversampled channelizer.
In this configuration, when the first input sample is delivered, the switch feeds this input to branch 0 and the channelizer computes the first set of output values. As more input samples come in, the switch moves in the counterclockwise direction through branches D−1, D−2, all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as the data keeps coming in. Every time the switch comes to the first branch 0, the channelizer outputs y0[m], y1[m], … , yM-1[m].
As more data keeps coming in and the switch feeds these samples to the first D addresses, the formal contents of these addresses are shifted to the next set of D addresses, and this process of data shift continues every time there is a new set of D input samples.
For every D input samples that are fed to the polyphase structure, the channelizer outputs M samples, y0[m], y1[m], … , yM-1[m]. This process increases the output sample rate from fs/M in the case of a maximally decimated channelizer, to fs/D in the case of a non-maximally decimated channelizer.
For more details, see [2].
After each D-point data sequence is delivered to the partitioned M-stage polyphase filter, the outputs of the M stages are computed and conditioned for delivery to the M-point FFT. The data shifting through the filter introduces frequency-dependent phase shift. To correct for this phase shift and alias all bands to DC, a circular shift buffer is inserted after the polyphase filters and before the M-point FFT.
With the commutator switch followed by M-stage polyphase filter, circular shift buffer, and a DFT matrix, the efficient implementation of the lowpass prototype-based filter bank looks like this.

References
[1] Harris, Fredric J, Multirate Signal Processing for Communication Systems, Prentice Hall PTR, 2004.
[2] Harris, F.J., Chris Dick, and Michael Rice. "Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications." IEEE® Transactions on Microwave Theory and Techniques. 51, no. 4 (2003).
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2017aWhen you select the Bands as separate output ports (Max. of 16 bands) parameter, the block outputs each narrowband signal at a separate port. The block can output a maximum of 16 narrowband signals separately. When you clear this parameter, the block concatenates all the narrowband signals to form a single output array.
You can now set the Decimation factor parameter to
Number of frequency bands. When you change the value
of the Number of frequency bands parameter, the decimation
factor changes automatically.
Existing Simulink models using the Channelizer block continue to run in R2024a.
Channelizer block supports input signals with arbitrary frame lengths when the:
Input signal is a fixed-size signal (frame length does not change during simulation) and you select the Allow arbitrary frame length for fixed-size input signals parameter
Input signal is a variable-size signal (frame length changes during simulation)
The frame length is arbitrary when it is not a multiple of the decimation factor.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)