dsp.AllpassFilter
Single section or cascaded allpass filter
Description
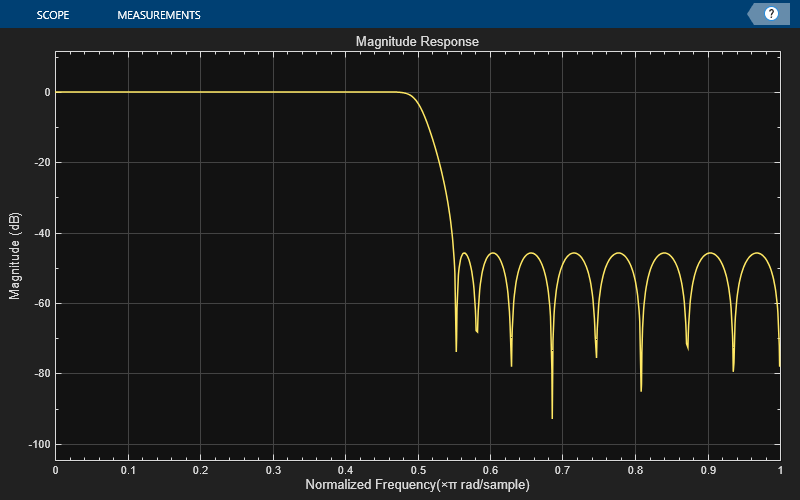
The dsp.AllpassFilter object filters each channel of the input using
allpass filter implementations. To import this object into Simulink®, use the MATLAB® System block.
To filter each channel of the input:
Create the
dsp.AllpassFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
Allpass = dsp.AllpassFilterAllpass, that filters each channel of the input signal
independently using an allpass filter, with the default structure and coefficients.
Allpass = dsp.AllpassFilter(Name=Value)Allpass, with each property set to the specified value
by one or more Name-Value pair arguments. Name
is the property name and Value is the corresponding value. For
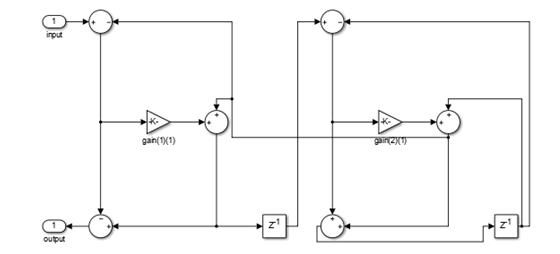
example, to set the filter structure as "Lattice", set
Structure to "Lattice".
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Regalia, Philip A. and Mitra Sanjit K. and Vaidyanathan, P. P. (1988) “The Digital All-Pass Filter: A Versatile Signal Processing Building Block.” Proceedings of the IEEE, Vol. 76, No. 1, 1988, pp. 19–37
[2] M. Lutovac, D. Tosic, B. Evans, Filter Design for Signal Processing Using MATLAB and Mathematica. Upper Saddle River, NJ: Prentice Hall, 2001.