designHalfbandIIR
Design and implement halfband IIR filter in the form of a coupled allpass filter
Since R2023b
Syntax
Description
[
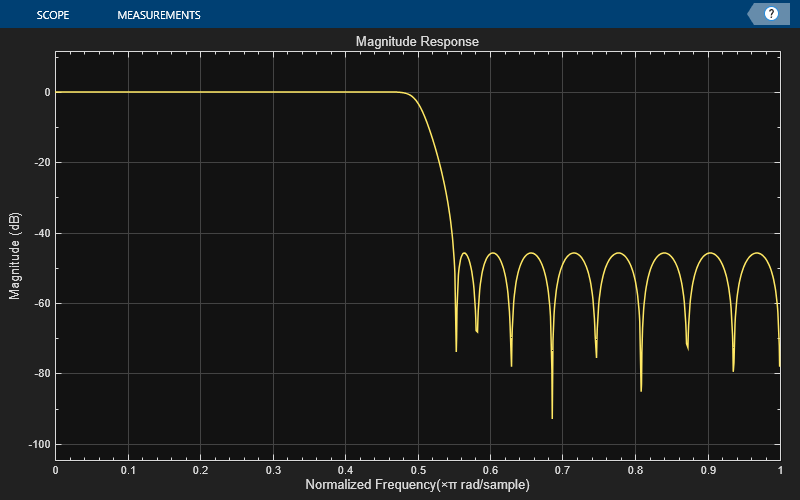
designs a halfband IIR filter in the form of a coupled allpass filter with the filter
order of 17 by using the Butterworth design method. The function completes any
unspecified design parameters with appropriate default values.a0,a1] = designHalfbandIIR
a0 and a1 are the polynomial coefficients
of the two allpass filters A0(z) and
A1(z). These filters form the two
branches of the coupled allpass filter. The transfer function of the IIR halfband filter
is given by:
The designHalfbandIIR function implements the allpass filters in
the minimum multiplier form. For more information, see Algorithms.
The System object™ argument is false by default. To implement the filter,
assign the filter coefficients in a0, a1 to
one of the supported System objects.
[
specifies options using one or more name-value arguments.a0,a1] = designHalfbandIIR(Name=Value)
For example, [
designs a halfband IIR filter with the filter order of 31 and transition width of 0.2 by
using the Elliptic window design method.a0,a1] =
designHalfbandIIR(FilterOrder=31,TransitionWidth=0.2,DesignMethod="ellip")
When you specify only a partial list of filter parameters, the function designs the filter by setting the other design parameters to their default values.
The function supports two design methods. Each design method supports a specific set
of design combinations. For more information, see DesignMethod.
This function supports code generation under certain conditions. For more information, see Code Generation.
filtObj = designHalfbandIIR(Name=Value)
This syntax applies when you set the SystemObject argument to
true.
Examples
Name-Value Arguments
Output Arguments
Algorithms
The designHalfbandIIR function models the IIR halfband filter in
the form of a coupled allpass filter using the minimum multiplier structure (single-rate
implementation) or in the form of an efficient polyphase structure (multirate
implementation).
The transfer function of the IIR halfband filter is
The transfer function of A0(z) and A1(z) in the elliptic form is
and
where N is the number of filter sections of the allpass filters A0(z) and A1(z).
Single-Rate Filter Implementation
When you set Structure to "single-rate", the
designHalfbandIIR function implements a coupled allpass filter
object comprising of a cascaded parallel structure of dsp.AllpassFilter and dsp.Delay filter objects.
This is a diagrammatic representation of the filter in the minimum multiplier form when
you set Structure to "single-rate". The structure
of the coupled allpass filter is composed of two allpass filters
A0(z) and
A1(z) connected in parallel. The
designHalfbandIIR function computes the overall filter output by
adding the output of the two respective branches.

You can design the filters A0(z) and A1(z) using the elliptic design method or the Butterworth design method.
Multirate Filter Implementation
When you set Structure to "interp" or
"decim", the function implements the filter using an efficient
two-branch polyphase structure. For more information on the polyphase implementation, see
the Algorithms section in the dsp.IIRHalfbandInterpolator and dsp.IIRHalfbandDecimator object pages.
References
[1] Orfanidis , SJ. High-Order Digital Parametric Equalizer Design. 2005, pp. 1026–46.