LTI System

Use linear time invariant system model object in Simulink

• 

Libraries:
Control System Toolbox

Description

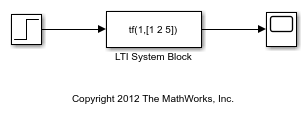
The LTI System block imports linear system model objects into the Simulink^® environment. You specify the LTI model to import in the LTI system variable parameter. You can import any type of proper linear time-invariant dynamic system model. If the imported system is a state-space (ss) model, you can specify initial state values in the Initial states parameter.

Examples

Simulate LTI Model in Simulink

The LTISystemBlockSimulation model shows how to use an LTI System block to simulate the response of a SISO transfer function to a step input.

• Open Model

Import MIMO LTI Model into Simulink

How to use an LTI System block to represent a MIMO linear system in Simulink®.

• Open Model

Ports

Input

Port_1(In1) — Input signal

scalar | vector

For a single-input LTI system, the input signal is a scalar. For multiple-input systems, combine the system inputs into a vector signal, using blocks such as:

• Mux (Simulink)

• Vector Concatenate (Simulink)

• Bus Creator (Simulink)

Output

Port_1(Out1) — Output signal

scalar | vector

For a single-output LTI system, the output signal is a scalar. For multiple-output systems, the output signal is a vector. To split system outputs into scalar signals, use blocks such as:

• Demux (Simulink)

• Bus Selector (Simulink)

Parameters

LTI system variable — Linear system

dynamic system model

Specify the linear system for the block as a MATLAB^® expression or a variable in the MATLAB workspace, the model workspace, or a data dictionary. The model can be SISO or MIMO.

Most linear time-invariant dynamic system models are supported, except:

• Frequency-response data models, such as frd and genfrd models.

• Nonlinear identified models, such as idnlarx.

• Models with unmodeled dynamics, such as udyn.

The specified model must be proper (see isproper).

The model can be either continuous time or discrete time. When the LTI system block is in a Simulink model with synchronous state control (see the State Control (HDL Coder) block), you must specify a discrete-time model.

Simulink converts the model to its state-space equivalent prior to initializing the simulation.

Initial states (state-space only) — Initial state values for state-space model

[] (default) | vector | scalar

If the linear system is in state-space form, specify the initial state values as a vector with as many entries as the system has states. If you specify a scalar value, the block applies that value to each state in the system. The default value, [], initializes all states to zero.

The concept of initial state is not well-defined for linear systems that are not in state-space form, such as transfer functions or zero-pole-gain models. For such models, the initial state depends on the choice of state coordinates used by the realization algorithm. As a result, the block ignores this parameter for such models.

Pade order (for linearization) — Order of Pade approximation

0 (default) | positive integer | vector

Set the order of the Pade approximation for linearization routines.

• The default value is 0, which results in a unity gain with no dynamic states.

• Setting the order to a positive integer n adds n states to your model, but results in a more accurate linear model of the delay.

Use a vector of positive integers to specify a different order for each input channel.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a

R2024a: Simulate state-space models with offsets

You can now simulate a state-space model with offsets using the LTI System block. Use the LTI system variable parameter to specify a state-space variable containing model offsets in the Offsets property. Offsets usually arise when linearizing nonlinear dynamics at some operating conditions. For more information about how to store offsets, see ss.

R2024a: Support for LTI models with complex coefficients

You can now simulate LTI models with complex coefficients using the LTI System block.