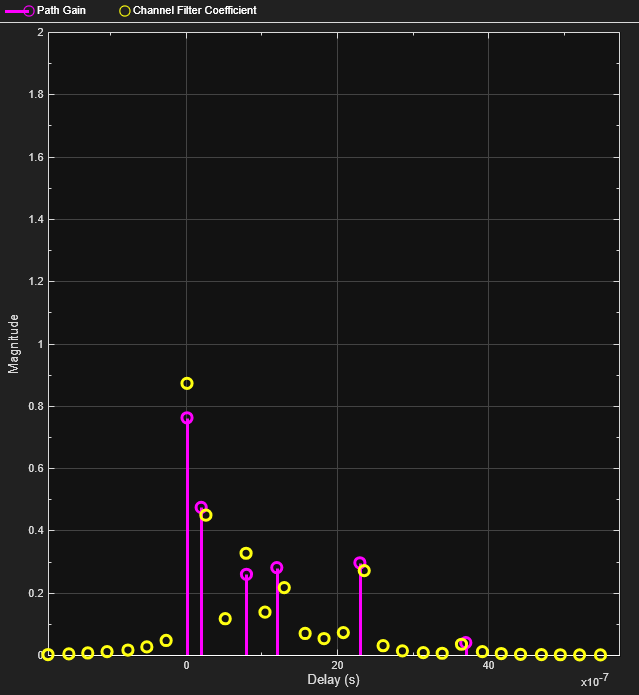
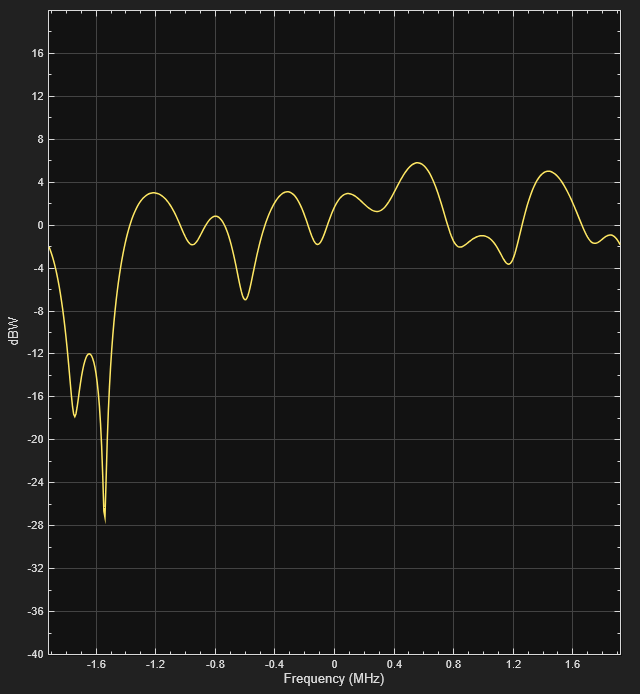
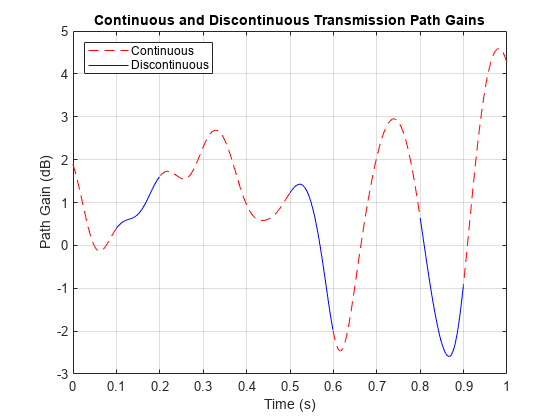
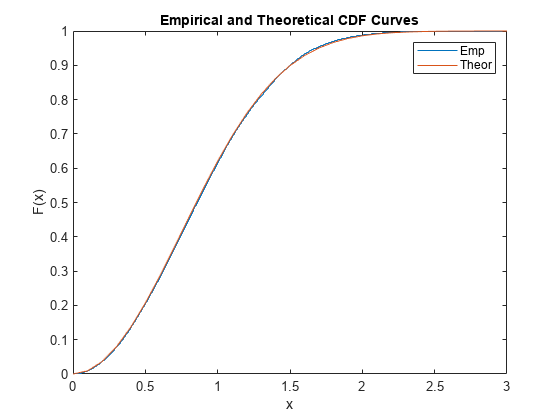
comm.RicianChannel
Filter input signal through multipath Rician fading channel
Description
The comm.RicianChannel
System object™ filters an input signal through a multipath Rician fading channel. For more
information on fading model processing, see the Methodology for Simulating
Multipath Fading Channels section.
To filter an input signal through a multipath Rician fading channel:
Create the
comm.RicianChannelobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
ricianchan = comm.RicianChannel
ricianchan = comm.RicianChannel(Name=Value)comm.RicianChannel(SampleRate=2) sets the input signal sample rate to
2.
Properties
Usage
Syntax
Description
Y = ricianchan(X)X through a multipath Rician fading channel
and returns the result in Y.
To enable this syntax, set the ChannelFiltering property
to true.
Y = ricianchan(X,inittime)
To enable this syntax, set the FadingTechnique property to
'Sum of sinusoids' and the InitialTimeSource
property to 'Input port'.
[
also returns the channel path gains of the underlying multipath Rician fading process in
Y,pathgains] = ricianchan(___)pathgains using any of the input argument combinations in the
previous syntaxes.
To enable this syntax, set the PathGainsOutputPort
property to true.
pathgains = ricianchan()
To enable this syntax, set the ChannelFiltering property
to false.
pathgains = ricianchan(inittime)
To enable this syntax, set the FadingTechnique property to
'Sum of sinusoids', the InitialTimeSource
property to 'Input port', and the ChannelFiltering property
to false.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Oestges, Claude, and Bruno Clerckx., MIMO Wireless Communications: From Real-World Propagation to Space-Time Code Design. 1st ed. Boston, MA: Elsevier, 2007.
[2] Correia, Luis M., and European Cooperation in the Field of Scientific and Technical Research (Organization), eds. Mobile Broadband Multimedia Networks: Techniques, Models and Tools for 4G. 1st ed. Amsterdam; Boston: Elsevier/Academic Press, 2006.
[3] Kermoal, J.P., L. Schumacher, K.I. Pedersen, P.E. Mogensen, and F. Frederiksen. “A Stochastic MIMO Radio Channel Model with Experimental Validation.” IEEE® Journal on Selected Areas in Communications 20, no. 6 (August 2002): 1211–26. https://doi.org/10.1109/JSAC.2002.801223.
[4] Jeruchim, Michel C., Philip Balaban, and K. Sam Shanmugan. Simulation of Communication Systems. Second edition. Boston, MA: Springer US, 2000.
[5] Patzold, M., Cheng-Xiang Wang, and B. Hogstad. “Two New Sum-of-Sinusoids-Based Methods for the Efficient Generation of Multiple Uncorrelated Rayleigh Fading Waveforms.” IEEE Transactions on Wireless Communications 8, no. 6 (June 2009): 3122–31. https://doi.org/10.1109/TWC.2009.080769.