geoTrajectory
Waypoint trajectory in geodetic coordinates
Description
The geoTrajectory
System object™ generates trajectories based on waypoints in geodetic coordinates. When you
create the System object, you can specify the time of arrival, velocity, and orientation at each
waypoint. The geoTrajectory
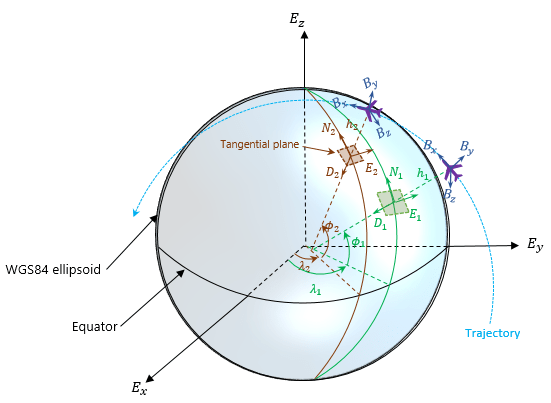
System object involves three coordinate systems. For more details, see Coordinate Frames in Geo Trajectory.
To generate an Earth-centered waypoint trajectory in geodetic coordinates:
Create the
geoTrajectoryobject and set its properties.Call the object as if it were a function.
To learn more about how System objects work, see What Are System Objects?.
Creation
Syntax
Description
trajectory = geoTrajectory(Waypoints,TimeOfArrival)geoTrajectory System object, trajectory,
based on the specified geodetic waypoints, Waypoints, and the
corresponding time, TimeOfArrival.
trajectory = geoTrajectory(Waypoints,TimeOfArrival,Name,Value)Name to the specified
Value. Unspecified properties and creation arguments have default or
inferred values.
Example: trajectory =
geoTrajectory([10,10,1000;10,11,1100],[0,3600]) creates a geodetic waypoint
trajectory System object, geojectory, that moves one degree in
longitude and 100 meters in altitude in one hour.
Creation Arguments
Creation arguments are properties which are set during creation of the System object and cannot be modified later. If you do not explicitly set a creation argument value, the property value is inferred.
You can specify Waypoints and TimeOfArrival as
value-only arguments or name-value pairs.
Properties
Usage
Description
[
outputs a frame of trajectory data based on specified creation arguments and properties,
where positionLLA,orientation,velocity,acceleration,angularVelocity,ecef2ref] = trajectory()trajectory is a geoTrajectory object.
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)