1903 Wright Flyer
This case study describes a model of the 1903 Wright Flyer. Built by Orville and Wilbur Wright, the Wright Flyer took to the skies in December 1903 and opened the age of controlled flight. The Wright brothers' flying machine achieved the following goals:
Left the ground under its own power
Moved forward and maintained its speed
Landed at an elevation no lower than where it started
Note
The final section of this study requires the Simulink 3D Animation software.
This model is based on an earlier simulation [1] that explored the longitudinal stability of the Wright Flyer and therefore modeled only forward and vertical motion along with the pitch angle. The Wright Flyer suffered from numerous engineering challenges, including dynamic and static instability. Laterally, the Flyer tended to overturn in crosswinds and gusts, and longitudinally, its pitch angle would undulate [2].
Under these constraints, the model recreates the longitudinal flight dynamics that pilots of the Wright Flyer would have experienced. Because they were able to control lateral motion, Orville and Wilbur Wright were able to maintain a relatively straight flight path.
Note, running this model generates information messages in the MATLAB® Command Window and assertion warning messages in the Diagnostic Viewer. This is because the model illustrates the use of the Assertion block to indicate that the flyer is hitting the ground when landing.
Wright Flyer Model
Open the Wright Flyer model by entering openExample('aeroblk_wf_3dof_noVR')
at the MATLAB command line.

Airframe Subsystem
The Airframe subsystem simulates the rigid body dynamics of the Wright Flyer airframe, including elevator angle of attack, aerodynamic coefficients, forces and moments, and three-degrees-of-freedom equations of motion.

The Airframe subsystem consists of the following parts:
Elevator Angle of Attack Subsystem
The Elevator Angle of Attack subsystem calculates the effective elevator angle for the Wright Flyer airframe and feeds its output to the Pilot subsystem.

Aerodynamic Coefficients Subsystem
The Aerodynamic Coefficients subsystem contains aerodynamic data and equations for calculating the aerodynamic coefficients, which are summed and passed to the Forces and Moments subsystem. Stored in data sets, the aerodynamic coefficients are determined by interpolation using Prelookup blocks.

Forces and Moments Subsystem
The aerodynamic forces and moments acting on the airframe are generated from aerodynamic coefficients. The Forces and Moments subsystem calculates the body forces and body moments acting on the airframe about the center of gravity. These forces and moments depend on the aerodynamic coefficients, thrust, dynamic pressure, and reference airframe parameters.

3DOF (Body Axes) Block
The 3DOF (Body Axes) block use equations of motion to define the linear and angular motion of the Wright Flyer airframe. It also performs conversions from the original model's axis system and the body axes.
3DOF (Body Axes) Block Parameters
![3DOF (Body Axes) block with parameters filled for 1903 Wright Flyer: units are English, mass type is Fixed, initial velocity is 47.26, initial body attitude is -(wf_alphaa-wf_incidence)*pi/180, initial incidence is wf_alphaa*pi/180, initial position is [0 -0.1], initial body rotation rate is wf_q, initial mass is wf_weight/wf_gravity, inertia is wf_inertia.](wright_airframe_3dof.png)
Environment Subsystem
The first and final flights of the Wright Flyer occurred on December 17, 1903. Orville and Wilbur Wright chose an area near Kitty Hawk, North Carolina, situated near the Atlantic coast. Wind gusts of more than 25 miles per hour were recorded that day. After the final flight on that blustery December day, a wind gust caught and overturned the Wright Flyer, damaging it beyond repair.
The Environment subsystem of the Wright Flyer model contains a variety of blocks from the Environment sublibrary of the Aerospace Blockset™ software, including wind, atmosphere, and gravity, and calculates airspeed and dynamic pressure. The Discrete Wind Gust Model block provides wind gusts to the simulated environment. The other blocks are
The Incidence & Airspeed block calculates the angle of attack and airspeed.
The COESA Atmosphere Model block calculates the air density.
The Dynamic Pressure block computes the dynamic pressure from the air density and velocity.
The WGS84 Gravity Model block produces the gravity at the Wright Flyer's latitude, longitude, and height.

Pilot Subsystem
The Pilot subsystem controls the aircraft by responding to both pitch angle (attitude) and angle of attack. If the angle of attack differs from the set angle of attack by more than one degree, the Pilot subsystem responds with a correction of the elevator (canard) angle. When the angular velocity exceeds +/- 0.02 rad/s, angular velocity and angular acceleration are also taken into consideration with additional corrections to the elevator angle.
Pilot reaction time largely determined the success of the flights [1]. Without an automatic controller, a reaction time of 0.06 seconds is optimal for successful flight. The Delay of Pilot (Variable Transport Delay) block recreates this effect by producing a delay of no more than 0.08 second.

Run the Simulation
The default values for this simulation allow the Wright Flyer model to take off and land successfully. The pilot reaction time (wf_B3) is set to 0.06 seconds, the desired angle of attack (wf_alphaa) is constant, and the altitude attained is low. The Wright Flyer model reacts similarly to the actual Wright Flyer. It leaves the ground, moves forward, and lands on a point as high as that from which it started. This model exhibits the longitudinal undulation in attitude of the original aircraft.
Attitude Scope (Measured in Radians)
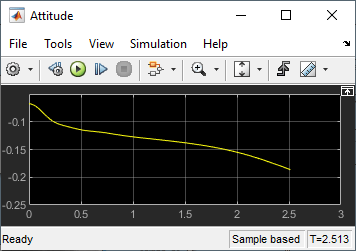
A pilot with quick reaction times and ideal flight conditions makes it possible to fly the Wright Flyer successfully. The Wright Flyer model confirms that controlling its longitudinal motion was a serious challenge. The longest recorded flight on that day lasted a mere 59 seconds and covered 852 feet.
Unreal Engine Visualization of the Wright Flyer
Note
This section requires the Simulink 3D Animation.
The Wright Flyer model offers visualization through Unreal Engine®. A 3D model is available in Virtual Reality Modeling Language (VRML) file format [3]. Simulation 3D Actor (Simulink 3D Animation) block reads and displays the 3D model, enabling a three-dimensional view of the flight motion.

References
[1] Hooven, Frederick J., “Longitudinal Dynamics of the Wright Brothers' Early Flyers: A Study in Computer Simulation of Flight,” from The Wright Flyer: An Engineering Perspective, ed. Howard S. Wolko, Smithsonian Institution Press, 1987.
[2] Culick, F. E. C. and H. R. Jex, “Aerodynamics, Stability, and Control of the 1903 Wright Flyer,” from The Wright Flyer: An Engineering Perspective, ed. Howard S. Wolko, Smithsonian Institution Press, 1987.
[3] Thaddeus Beier created the initial Wright Flyer model in Inventor format, and Timothy Rohaly converted it to VRML.
See Also
3DOF (Body Axes) | Incidence & Airspeed | COESA Atmosphere Model | Dynamic Pressure | WGS84 Gravity Model