Leveraging Stochastic Processes | Understanding Discrete-Event Simulation, Part 3
From the series: Understanding Discrete-Event Simulation
Learn how discrete-event simulation uses stochastic processes, in which aspects of a system are randomized, in this MATLAB® Tech Talk by Will Campbell. Stochastic processes are particularly important to discrete-event simulation, as they are a method you can use to approximate the details of a system that you either can’t or choose not to model. The video explores why you would choose different random distributions, and why you would mix determinism and non-determinism. It explores how careful placement of probabilistic terms enables you to conduct meaningful analyses without overcomplicating the model.
Published: 6 Jul 2017
Let’s discuss stochastic processes in the context of discrete-event simulation. A stochastic process is one in which aspects of the system are randomized. Since there is no definitive outcome as to how the processes will evolve over time, they are often referred to as "non-deterministic." Stochastic processes are particularly important to discrete-event simulation as a method of approximating the details of a system that we either can’t or choose not to model. If we neglect these details altogether and define all the parameters of our model as constants, the simulation would be trivial and uninformative.
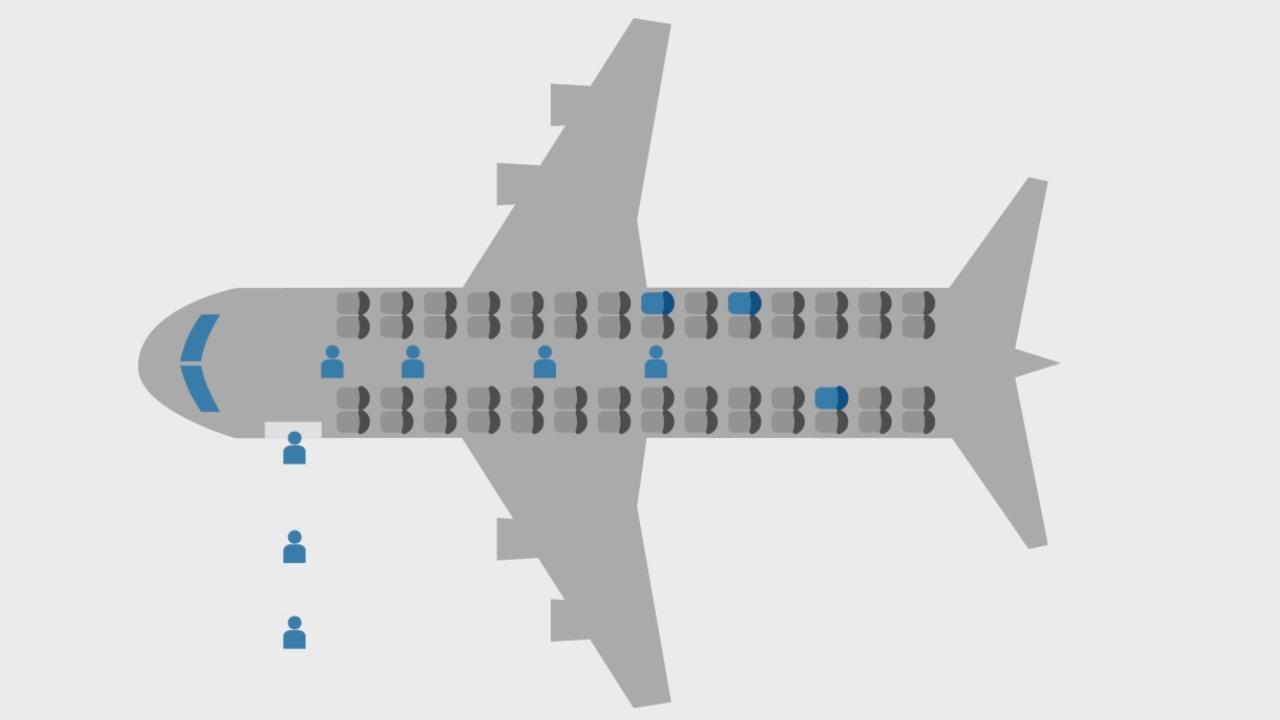
To illustrate this concept, consider a discrete-event simulation of passengers boarding an aircraft. One way to achieve this is to model the aisle as a series of queues and servers that the entities, in this case the passengers, move through until they reach their assigned seat. When they reach the correct row, passengers stow their carry-ons in the overhead bin before working their way into their seat. All you have to do is define the time necessary for each passenger to complete these tasks in order to simulate how long it takes for the plane to completely board.
A first-order approximation of this process is to assume that every passenger takes the exact same amount of time to complete the task of stowing carry-ons and getting into their seat. But we all know from personal experience that this is not the case; some people are just slower than others. A simulation should therefore model variability in task durations to provide more meaningful results. The question is how best to go about this. We can’t possibly model every nuance of a person’s behavior as they get situated in their seat. But, we can move closer to reality by randomizing the time each passenger spends in the servers.
Now of course, we have to put some constraints on the model so that the randomized values are reasonable. We can accomplish this by defining a probability distribution for the time an entity spends in a server. The distribution is just the odds of a particular number being selected. One strategy would be to use a uniform distribution in which the same odds are placed on every value within a specified range. In our case, we could say that it takes passengers between 2 and 10 seconds to get in their seat.
But if you actually measured the time passengers spent completing this task, you might find that more of them clump around a particular value in the middle of this range, while fewer are found at the extremes. This is a common statistical result, which is why you often see Gaussian or normal distributions used in models. However, in the case of passenger loading, a Gaussian distribution probably isn’t the best choice. Since it’s impossible for a task to take less than zero seconds, a Poisson or Weibull distribution might make more sense. But whatever distribution you opt for is going to depend on the phenomenon you’re attempting to characterize.
Now it’s not all or nothing when it comes to employing probability in discrete-event simulations. You choose how much to model deterministically and rely on probability to fill in the rest. In general, you want to focus on including system details that don’t conform well to a probability distribution. For instance, the time required to get into a seat on a plane depends heavily on whether or not a seated passenger is in the way. If that person has to get up to make room, the duration of the seating process increases significantly. So in this case, you’d really want to employ probabilities specific to the situation instead of a single, blanket rule.
It’s this technique of mixing determinism and non-determinism that makes discrete-event simulations so valuable. Judicious placement of probabilistic terms enables you to conduct meaningful analyses without overcomplicating the model.