orthfilt
Orthogonal wavelet filters
Description
Examples
Input Arguments
Output Arguments
Algorithms
For an orthogonal wavelet in the multiresolution framework, start with the scaling function ϕ and the wavelet function ψ. One of the fundamental relations is the twin-scale relation:
All the filters used in the dwt and idwt functions are intimately related to the sequence . If ϕ is compactly supported, the sequence
(wn) is finite and can be viewed as an
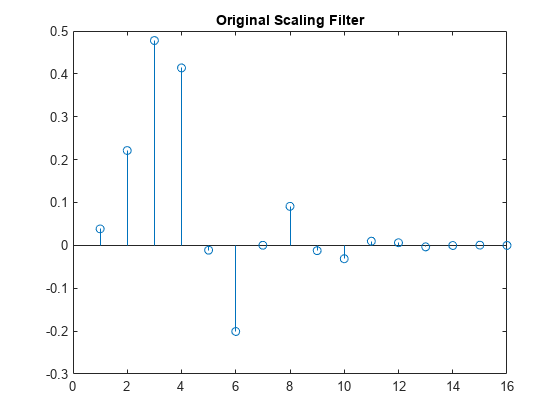
FIR filter. The scaling filter W is a lowpass FIR filter of length
2N, with the sum 1, and with the norm of 1/√2.
For example, for a db3 scaling filter,
w = dbwavf("db3")
w = 0.2352 0.5706 0.3252 -0.0955 -0.0604 0.0249
sum(w)
= 1.000
norm(w)
= 0.7071
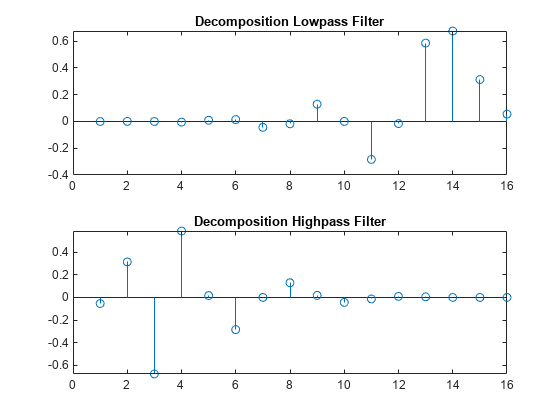
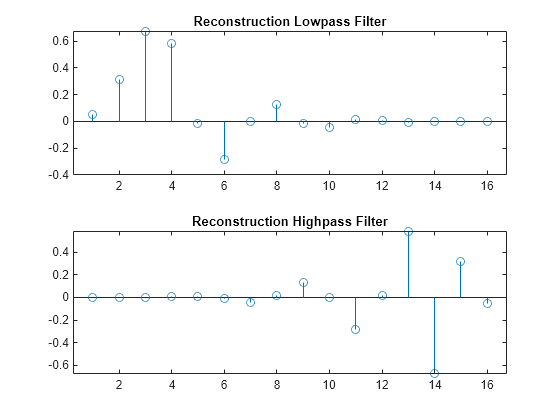
Define four FIR filters from filter W of length 2N and norm
1.
The function computes the four filters using the following scheme.

HiR and LoR are quadrature mirror filters:
HiR(k) = (-1)kLoR(2N + 1 -
k), for k = 1, 2, … , 2N. Because wrev reverses vectors, HiD and
LoD are also quadrature mirror filters.
References
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
Extended Capabilities
Version History
Introduced before R2006a