dlicwt

Deep learning inverse continuous 1-D wavelet transform

Since R2024b

Syntax

x = dlicwt(cfs,psifvec,filteridx)

x = dlicwt(cfs,psifvec,filteridx,DataFormat=fmt)

Description

x = dlicwt(cfs,psifvec,filteridx) inverts the continuous wavelet transform (CWT) coefficient matrix cfs using the reduced-weight CWT filter bank psifvec and bookkeeping matrix filteridx. The dlicwt function requires Deep Learning Toolbox™.

x = dlicwt(cfs,psifvec,filteridx,DataFormat=fmt) specifies the data format of cfs.

Examples

Invert Deep Learning Continuous Wavelet Transform of Multisignal

Load the Espiga3 EEG dataset. The data consists of 23 channels of EEG sampled at 200 Hz. There are 995 samples in each channel. Save the multisignal as a dlarray, specifying the dimensions in order. dlarray permutes the array dimensions to the "CBT" shape expected by a deep learning network.

load Espiga3
Fs = 200;
[N,ch] = size(Espiga3);
dlx = dlarray(Espiga3,"TCB");
whos Espiga3 dlx

  Name           Size                Bytes  Class      Attributes

  Espiga3      995x23               183080  double               
  dlx           23x1x995            183110  dlarray              

dims(dlx)

ans = 
'CBT'

Create a CWT filter bank that is compatible with the channels. Specify periodic boundary conditions. Then use the cwtfilters2array function to convert the filter bank to a reduced-weight tensor suitable for deep learning. Include the lowpass filter in the tensor.

fb = cwtfilterbank(SignalLength=N,SamplingFrequency=Fs, ...
    Boundary="periodic");
[psifvec,filteridx] = cwtfilters2array(fb,IncludeLowpass=true);

Obtain the deep learning CWT of the multisignal.

dlcfs = dlcwt(dlx,psifvec,filteridx);
whos dlcfs

  Name        Size                     Bytes  Class      Attributes

  dlcfs      72x23x1x995            26363528  dlarray    complex   

dims(dlcfs)

ans = 
'SCBT'

To reconstruct the signal, compute the deep learning inverse CWT.

dlxrec = dlicwt(dlcfs,psifvec,filteridx);
whos dlxrec

  Name         Size                Bytes  Class      Attributes

  dlxrec      23x1x995            183086  dlarray              

dims(dlxrec)

ans = 
'CBT'

Convert the output to a numeric array. To match the dimensions of the original multisignal, permute the output dimensions to correspond with the "TCB" format. The result is a matrix because there is only one batch.

xrec = extractdata(dlxrec);
xrec = permute(xrec,[3 1 2]);
whos xrec Espiga3

  Name           Size             Bytes  Class     Attributes

  Espiga3      995x23            183080  double              
  xrec         995x23            183080  double              

Choose two of the channels. Compare the original channel with its reconstruction.

channelIdx = [2 6];
tiledlayout(2,1)
for k=1:2
    idx = channelIdx(k);
    nexttile
    xorig = Espiga3(:,idx);
    xreco = xrec(:,idx);
    plot(xorig)
    ylabel("Channel "+num2str(idx))
    hold on
    plot(xreco,"--")
    hold off
    legend("Original","Reconstruction")
    title("MSE: "+mean((xorig-xreco).^2))
    grid on
end

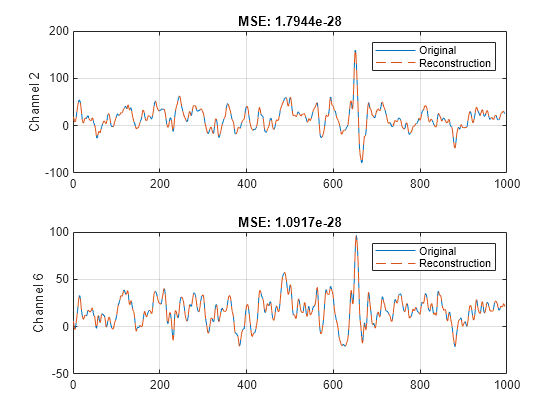
Input Arguments

cfs — Continuous wavelet transform

dlarray object | numeric array

Continuous wavelet transform, specified as a formatted or unformatted dlarray (Deep Learning Toolbox) or numeric array. cfs is the CWT of a real-valued signal.

• If cfs if a formatted dlarray, it must be in the "SCBT" or "CBT" format.

• If cfs is in the "CBT" format, the dlicwt function unflattens cfs to the "SCBT" shape.

• If cfs is real-valued, the number of channels C must be even because the dlicwt function assumes that the true number of channels is C/2.

• If cfs is an unformatted dlarray, it must be compatible with the "SCBT" or "CBT" formats and you must set DataFormat.

The dlicwt function computes the inverse CWT along the "S" dimension of cfs. The "S" dimension corresponds to scale, or equivalently, the center frequency of the wavelet bandpass filters.

Data Types: single | double
Complex Number Support: Yes

psifvec — Reduced-weight CWT filter bank

dlarray object | numeric array

Reduced-weight CWT filter bank, specified as a real-valued 1-by-1-by-Nr tensor, where Nr is the number of weights in the filter bank. Use cwtfilters2array to obtain psifvec.

Data Types: single | double

filteridx — Bookkeeping matrix

matrix

Bookkeeping matrix, specified as a matrix. In order to invert the CWT, the dlicwt function uses filteridx and psifvec to reconstruct an approximation to the CWT filter bank. Use cwtfilters2array to obtain filteridx.

You can use array2cwtfilters to reconstruct the CWT filter bank from psifvec and filteridx.

fmt — CWT format

character vector | string scalar

CWT format, specified as a character vector or string scalar. This argument is valid only if cfs is unformatted.

Each character in this argument must be one of these labels:

• "S" —Spatial (scale) dimension

• "C" — Channel

• "B" — Batch observations

• "T" — Time

The dlicwt function accepts any permutation of "CBT" or "SCBT". Each element of the argument labels the matching dimension of cfs. You can specify at most one of each of the "S", "C", "B", and "T" labels.

Example: x = dlicwt(cfs,psifvec,filteridx,DataFormat="SBCT") specifies the format of the unformatted dlarray object cfs as "SBCT".

Output Arguments

x — Reconstructed signal

dlarray object

Reconstructed signal, returned as a formatted or unformatted dlarray object.

• If cfs is a formatted dlarray, then x is a "CBT" formatted dlarray.

• If cfs is an unformatted dlarray, then x is an unformatted dlarray. The dimension order in x is "CBT".

Data Types: single | double

Version History

Introduced in R2024b