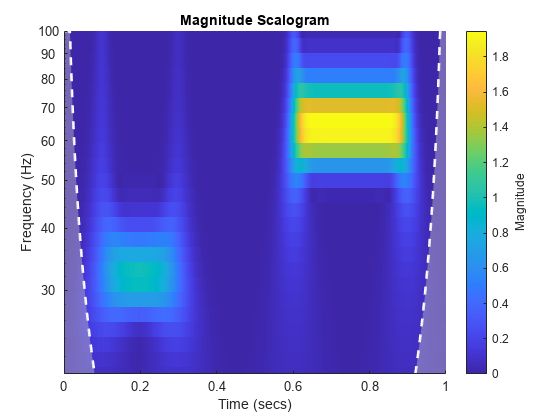
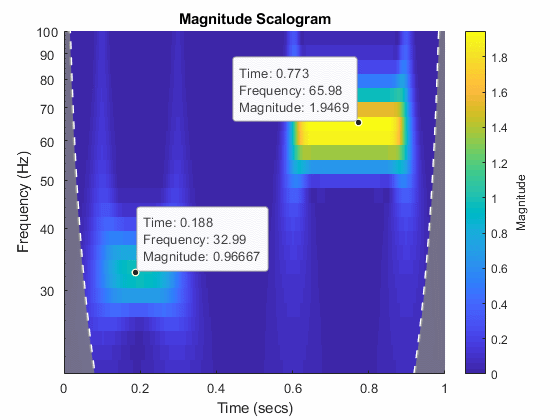
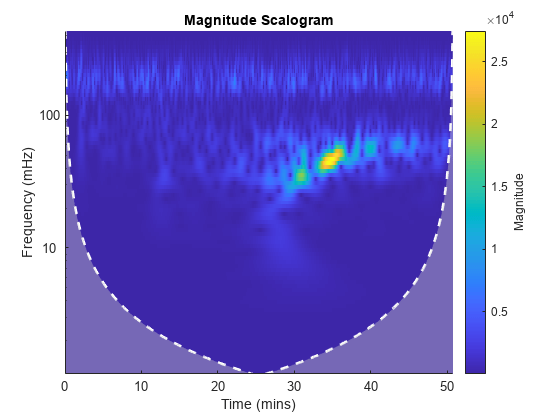
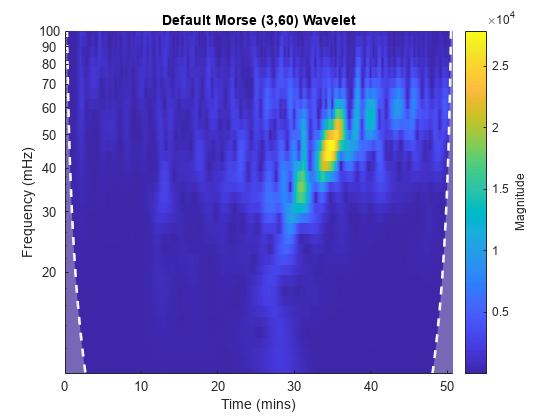
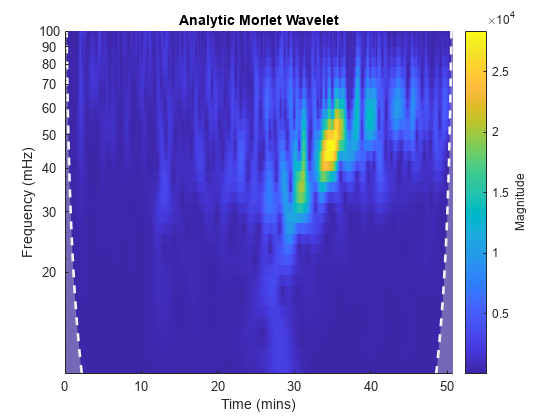
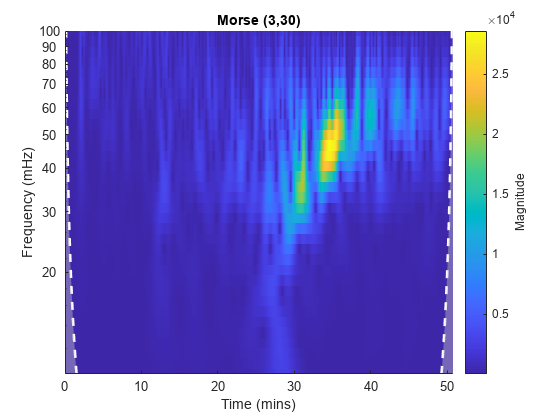
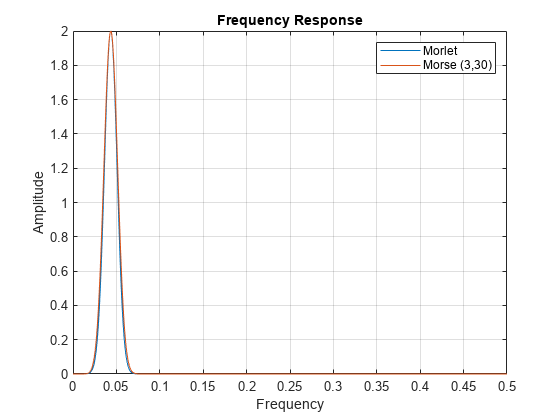
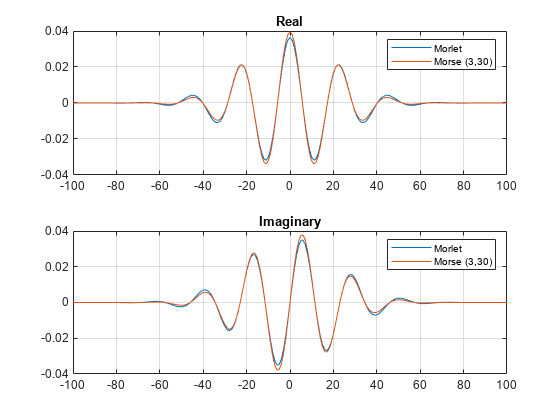
cwtfilterbank
Continuous wavelet transform filter bank
Description
Use cwtfilterbank to create a continuous wavelet
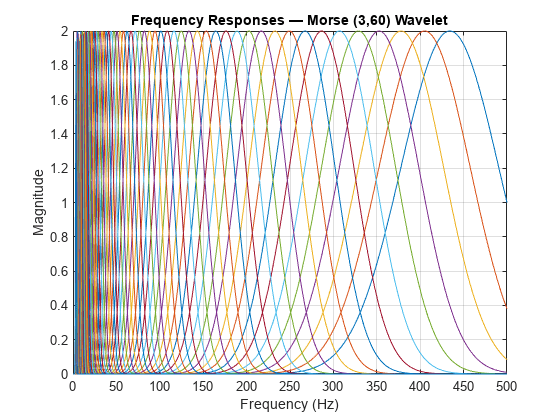
transform (CWT) filter bank. The default wavelet used in the filter bank is the analytic
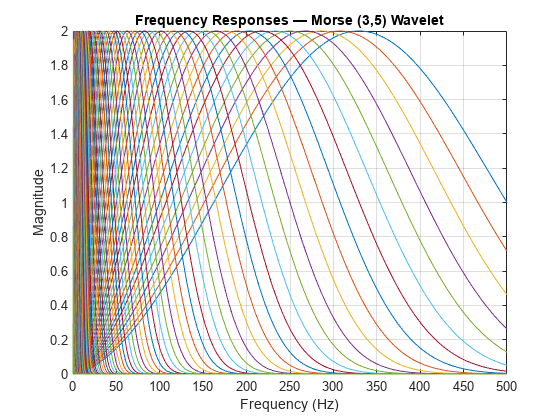
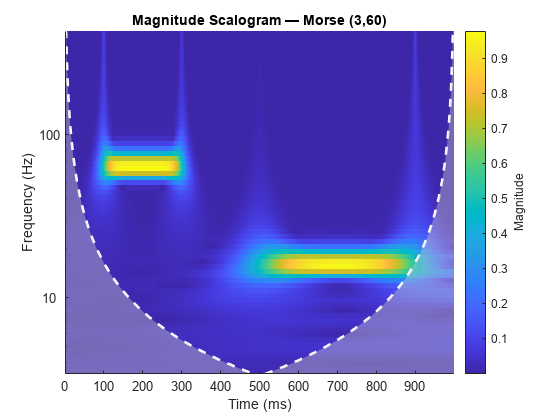
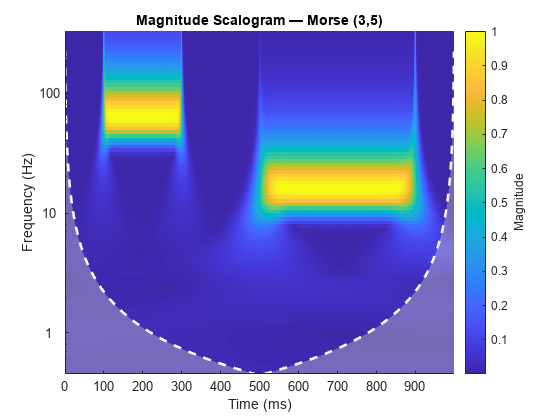
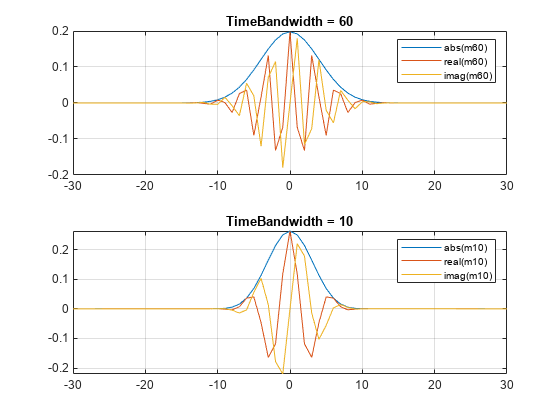
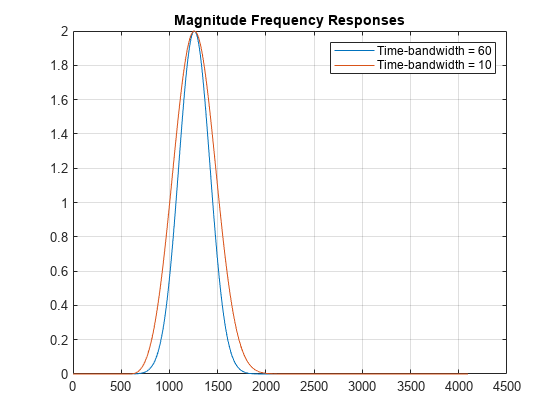
Morse (3,60) wavelet. You can vary the time-bandwidth and symmetry parameters for the
Morse wavelets, to tune the Morse wavelet for your needs. You can also use the analytic
Morlet (Gabor) wavelet or bump wavelet. When analyzing multiple signals in
time-frequency, for improved computational efficiency, you can precompute the filters
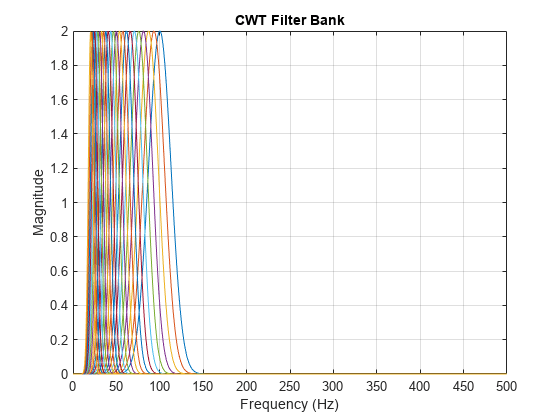
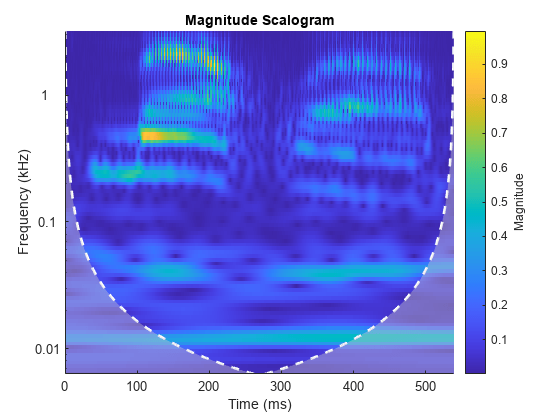
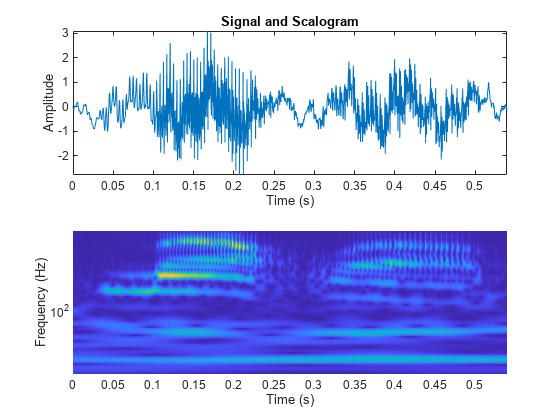
once and then pass the filter bank as input to cwt. With the filter bank, you can visualize wavelets in time and
frequency. You can also create filter banks with specific frequency or period ranges,
and measure 3-dB bandwidths. You can determine the quality factor for the wavelets in
the filter bank.
Creation
Description
fb = cwtfilterbankfb. The
filters are normalized so that the peak magnitudes for all passbands are
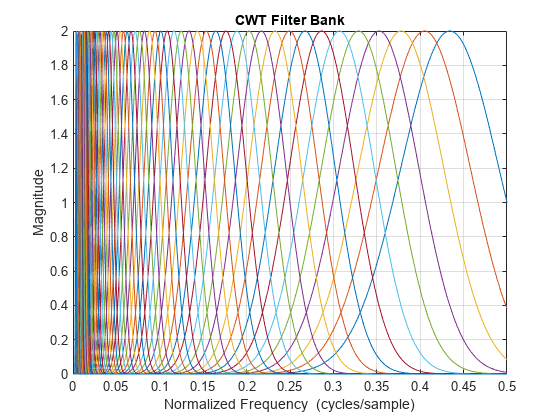
approximately equal to 2. The default filter bank is designed for a signal
with 1024 samples. The default filter bank uses the analytic Morse (3,60)
wavelet. The filter bank uses the default scales: approximately 10 wavelet
bandpass filters per octave (10 voices per octave). The highest-frequency
passband is designed so that the magnitude falls to half the peak value at
the Nyquist frequency.
As implemented, the CWT uses L1 normalization. With L1 normalization, equal amplitude oscillatory components at different scales have equal magnitude in the CWT. L1 normalization provides a more accurate representation of the signal. The amplitudes of the oscillatory components agree with the amplitudes of the corresponding wavelet coefficients. See Sinusoid and Wavelet Coefficient Amplitudes.
fb can be used as input for cwt.
fb = cwtfilterbank(Name=Value)fb with Properties using
one or more name-value arguments. Properties can be specified in any order
as Name1=Value1,...,NameN=ValueN.
Note
You cannot change a property value of an existing filter bank. For
example, if you have a filter bank fb with a
SignalLength of 2000, you must create a
second filter bank fb2 to process a signal with
2001 samples. You cannot assign a different
SignalLength to fb.
Properties
Object Functions
wt | Continuous wavelet transform with filter bank |
freqz | CWT filter bank frequency responses |
timeSpectrum | Time-averaged wavelet spectrum |
scaleSpectrum | Scale-averaged wavelet spectrum |
wavelets | CWT filter bank time-domain wavelets |
scales | CWT filter bank scales |
waveletsupport | CWT filter bank time supports |
qfactor | CWT filter bank quality factor |
powerbw | CWT filter bank 3 dB bandwidths |
centerFrequencies | CWT filter bank bandpass center frequencies |
centerPeriods | CWT filter bank bandpass center periods |
Examples
Tips
The first time you use a filter bank to take the CWT of a signal, the wavelet filters are constructed to have the same datatype as the signal. A warning message is generated when you apply the same filter bank to a signal with a different datatype. Changing datatypes comes with the cost of redesigning or changing the precision of the filter bank. For optimal performance, use a consistent datatype.
When performing multiple CWTs, for example inside a for-loop, the recommended workflow is to first create a
cwtfilterbankobject and then use thewtobject function. This workflow minimizes overhead and maximizes performance. See Using CWT Filter Bank on Multiple Time Series.
References
[1] Lilly, J. M., and S. C. Olhede. “Generalized Morse Wavelets as a Superfamily of Analytic Wavelets.” IEEE Transactions on Signal Processing. Vol. 60, No. 11, 2012, pp. 6036–6041.
[2] Lilly, J. M., and S. C. Olhede. “Higher-Order Properties of Analytic Wavelets.” IEEE Transactions on Signal Processing. Vol. 57, No. 1, 2009, pp. 146–160.
[3] Lilly, J. M. jLab: A data analysis package for MATLAB®, version 1.6.2. 2016. http://www.jmlilly.net/jmlsoft.html.
[4] Lilly, J. M. “Element analysis: a wavelet-based method for analysing time-localized events in noisy time series.” Proceedings of the Royal Society A. Volume 473: 20160776, 2017, pp. 1–28. dx.doi.org/10.1098/rspa.2016.0776.