assignDetectionsToTracks
Assign detections to tracks for multiobject tracking
Syntax
Description
[
assigns detections to tracks in the context of multiple object tracking using
the James Munkres's variant of the Hungarian assignment algorithm. It also
determines which tracks are missing and which detections should begin new
tracks. It returns the indices of assigned and unassigned tracks, and unassigned
detections. The assignments,unassignedTracks,unassignedDetections]
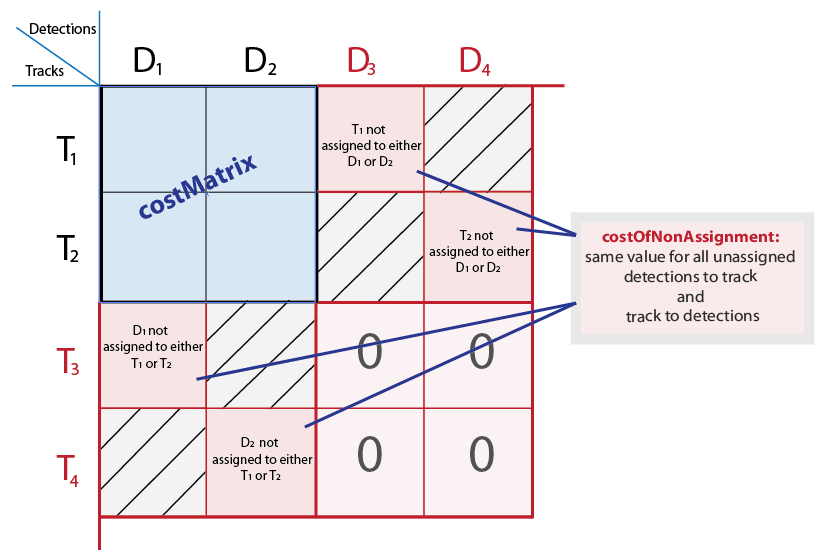
= assignDetectionsToTracks(costMatrix,costOfNonAssignment)costMatrix must be an
M-by-N matrix. In this matrix,
M represents the number of tracks, and
N is the number of detections. Each value represents the
cost of assigning the Nth
detection to the Mth track. The
lower the cost, the more likely that a detection gets assigned to a track. The
costOfNonAssignment scalar input represents the cost of
a track or a detection remaining unassigned.
[ specifies
the cost of unassigned tracks and detections separately. The assignments,unassignedTracks,unassignedDetections]
= assignDetectionsToTracks(costMatrix, unassignedTrackCost,unassignedDetectionCost)unassignedTrackCost must
be a scalar value, or an M-element vector, where M represents
the number of tracks. For the M-element vector,
each element represents the cost of not assigning any detection to
that track. The unassignedDetectionCost must
be a scalar value or an N-element vector, where N represents
the number of detections.
Examples
Input Arguments
Output Arguments
References
[1] Miller, Matt L., Harold S. Stone, and Ingemar J. Cox, “Optimizing Murty's Ranked Assignment Method,” IEEE Transactions on Aerospace and Electronic Systems, 33(3), 1997.
[2] Munkres, James, “Algorithms for Assignment and Transportation Problems,” Journal of the Society for Industrial and Applied Mathematics, Volume 5, Number 1, March, 1957.
Extended Capabilities
Version History
Introduced in R2012b