Mapped SI Engine
Spark-ignition engine model using lookup tables
Libraries:
Powertrain Blockset /
Propulsion /
Combustion Engines
Vehicle Dynamics Blockset /
Powertrain /
Propulsion
Description
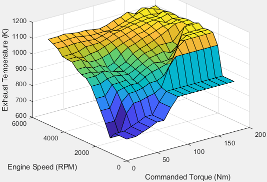
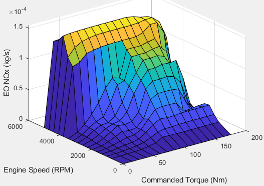
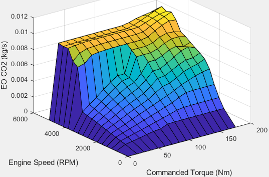
The Mapped SI Engine block implements a mapped spark-ignition (SI) engine model using power, air mass flow, fuel flow, exhaust temperature, efficiency, and emission performance lookup tables. You can use the block for:
Hardware-in-the-loop (HIL) engine control design
Vehicle-level fuel economy and performance simulations
The block enables you to specify lookup tables for these engine characteristics. The lookup tables, developed with the Model-Based Calibration Toolbox™, are functions of commanded torque, Tcmd, brake torque, Tbrake, and engine speed, N. If you select Input engine temperature, the tables are also a function of engine temperature, TempEng.
| Table | Input Engine Temperature Parameter Setting | |
|---|---|---|
off | on | |
Power | ƒ(Tcmd,N) | ƒ(Tcmd,N,TempEng) |
Air | ƒ(Tbrake,N) | ƒ(Tbrake,N,TempEng) |
Fuel | ||
Temperature | ||
Efficiency | ||
HC | ||
CO | ||
NOx | ||
CO2 | ||
PM | ||
To bound the Mapped SI Engine block output, the block does not extrapolate the lookup table data.
Virtual Calibration
If you have Model-Based Calibration Toolbox, click Calibrate Maps to virtually calibrate the 2D lookup tables using measured data. The dialog box steps through these tasks.
Task | Description | ||||
|---|---|---|---|---|---|
Import firing data | Import this loss data from a file. For example, open
For more information, see Using Data (Model-Based Calibration Toolbox).
Collect firing data at steady-state operating conditions when injectors deliver the fuel. Data should cover the engine speed and torque operating range. Model-Based Calibration Toolbox uses the firing data boundary as the maximum torque. To filter or edit the data, select Edit in Application. The Model-Based Calibration Toolbox Data Editor opens. | ||||
Import non-firing data | Import this non-firing data from a file. For example, open
Collect non-firing (motoring) data at steady-state operating conditions when fuel is cut off. All non-firing torque points must be less than zero. Non-firing data is a function of engine speed only. | ||||
Generate response models | For both firing and non-firing data, the Model-Based Calibration Toolbox uses test plans to fit data to Gaussian process models (GPMs). To assess or adjust the response model fit, select Edit in Application. The Model-Based Calibration Toolbox Model Browser opens. For more information, see Model Assessment (Model-Based Calibration Toolbox). | ||||
Generate calibration | Model-Based Calibration Toolbox calibrates the firing and non-firing response models and generates calibrated tables. To assess or adjust the calibration, select Edit in Application. The Model-Based Calibration Toolbox CAGE Browser opens. For more information, see Calibration Lookup Tables (Model-Based Calibration Toolbox). | ||||
Update block parameters | Update the block lookup table and breakpoint parameters with the calibration. |
Cylinder Air Mass
The block calculates the normalized cylinder air mass using these equations.
The equations use these variables.
| L | Normalized cylinder air mass |
Nominal engine cylinder air mass at standard temperature and pressure, piston at bottom dead center (BDC) maximum volume, in kg | |
Crankshaft revolutions per power stroke, rev/stroke | |
| Standard pressure | |
| Standard temperature | |
Ideal gas constant for air and burned gas mixture | |
Displaced volume | |
Number of engine cylinders | |
| N | Engine speed |
Engine air mass flow, in g/s |
Turbocharger Lag
To model turbocharger lag, select Include turbocharger lag effect. During throttle control, the time constant models the manifold filling and emptying dynamics. When the torque request requires a turbocharger boost, the block uses a larger time constant to represent the turbocharger lag. The block uses these equations.
|
Dynamic torque |
|
|
Boost time constant |
|
|
Final time constant |
|
The equations use these variables.
| Tbrake |
Brake torque |
| Tstdy | Steady-state target torque |
| τbst |
Boost time constant |
| τbst,rising, τbst,falling |
Boost rising and falling time constant, respectively |
| τeng |
Final time constant |
| τthr | Time constant during throttle control |
| ƒbst(N) | Boost torque speed line |
| N | Engine speed |
Fuel Flow
To calculate the fuel economy for high-fidelity models, the block uses the volumetric fuel flow.
The equation uses these variables.
| Fuel mass flow | |
| Sgfuel | Specific gravity of fuel |
| Qfuel | Volumetric fuel flow |
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Crankshaft power | |
|
|
| Fuel input power | ||
| Power loss | |||
|
| Not used | |||
The equations use these variables.
LHV | Fuel lower heating value |
ω | Engine speed, rad/s |
| Fuel mass flow | |
τeng | Fuel mass per injection time constant |
Examples
Ports
Input
Output
Parameters
Extended Capabilities
Version History
Introduced in R2017a