Splitting Categorical Predictors in Classification Trees
Challenges in Splitting Multilevel Predictors
When you grow a classification tree, finding an optimal binary split for a categorical predictor with many levels is more computationally challenging than finding a split for a continuous predictor. For a continuous predictor, a tree can split halfway between any two adjacent, unique values of the predictor. In contrast, to find an exact, optimal binary split for a categorical predictor with L levels, a classification tree must consider 2L–1–1 splits. To obtain this formula:
Count the number of ways to assign L distinct values to the left and right nodes. There are 2L ways.
Divide 2L by 2, because left and right can be swapped.
Discard the case that has an empty node.
For regression problems and binary classification problems, the software uses the exact search algorithm through a computational shortcut[1]. The tree can order the categories by mean response (for regression) or class probability for one of the classes (for classification). Then, the optimal split is one of the L – 1 splits for the ordered list. Therefore, computational challenges arise only when you grow classification trees for data with K ≥ 3 classes.
Algorithms for Categorical Predictor Split
To reduce computation, the software offers several heuristic algorithms for
finding a good split. You can choose an algorithm for splitting categorical
predictors by using the 'AlgorithmForCategorical' name-value
pair argument when you grow a classification tree using fitctree or when you create a classification learner using templateTree for a classification ensemble (fitcensemble) or a multiclass ECOC model (fitcecoc).
If you do not specify an algorithm, the software selects the optimal algorithm
for each split using the known number of classes and levels of a categorical
predictor. If the predictor has at most MaxNumCategories
levels, the software splits categorical predictors using the exact search algorithm.
Otherwise, the software chooses a heuristic search algorithm based on the number of
classes and levels. The default MaxNumCategories level is 10.
Depending on your platform, the software cannot perform an exact search on
categorical predictors with more than 32 or 64 levels.
The available heuristic algorithms are: pull left by purity, principal component-based partitioning, and one-versus-all by class.
Pull Left by Purity
The pull left by purity algorithm starts with all L categorical levels on the right branch. The algorithm then takes these actions:
Inspect the K categories that have the largest class probabilities for each class.
Move the category with the maximum value of the split criterion to the left branch.
Continue moving categories from right to left, recording the split criterion at each move, until the right child has only one category remaining.
Out of this sequence, the selected split is the one that maximizes the split criterion.
Select this algorithm by specifying
'AlgorithmForCategorical','PullLeft' in fitctree or templateTree.
Principal Component-Based Partitioning
The principal component-based partitioning algorithm[2] finds a close-to-optimal binary partition of the L predictor levels by searching for a separating hyperplane. The hyperplane is perpendicular to the first principal component of the weighted covariance matrix of the centered class probability matrix.
The algorithm assigns a score to each of the L categories, computed as the inner product between the found principal component and the vector of class probabilities for that category. Then, the selected split is one of the L – 1 splits that maximizes the split criterion.
Select this algorithm by specifying
'AlgorithmForCategorical','PCA' in fitctree or templateTree.
One-Versus-All by Class
The one-versus-all by class algorithm starts with all L categorical levels on the right branch. For each of the K classes, the algorithm orders the categories based on their probability for that class.
For the first class, the algorithm moves each category to the left branch in order, recording the split criterion at each move. Then the algorithm repeats this process for the remaining classes. Out of this sequence, the selected split is the one that maximizes the split criterion.
Select this algorithm by specifying
'AlgorithmForCategorical','OVAbyClass' in fitctree or templateTree.
Inspect Data with Multilevel Categorical Predictors
This example shows how to inspect a data set that includes categorical predictors with many levels (categories) and how to train a binary decision tree for classification.
Load Sample Data
Load the census1994 file. This data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 a year. Specify a cell array of character vectors containing the variable names.
load census1994
VarNames = adultdata.Properties.VariableNames;Some variable names in the adultdata table contain the _ character. Replace instances of _ with a space.
VarNames = strrep(VarNames,'_',' ');
Specify the predictor data tbl and the response vector Y.
tbl = adultdata(:,1:end-1); Y = categorical(adultdata.salary);
Inspect Categorical Predictors
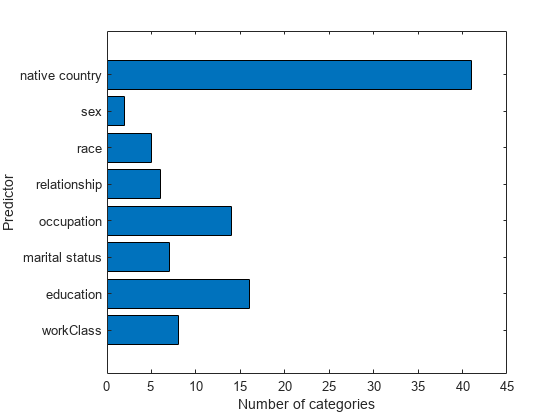
Some categorical variables have many levels (categories). Count the number of levels of each categorical predictor.
Find the indexes of categorical predictors that are not numeric in the tbl table by using varfun and isnumeric. The varfun function applies the isnumeric function to each variable of the table tbl.
cat = ~varfun(@isnumeric,tbl,'OutputFormat','uniform');
Define an anonymous function to count the number of categories in a categorical predictor using numel and categories.
countNumCats = @(var)numel(categories(categorical(var)));
The anonymous function countNumCats converts a predictor to a categorical array, then counts the unique, nonempty categories of the predictor.
Use varfun and countNumCats to count the number of categories for the categorical predictors in tbl.
numCat = varfun(@(var)countNumCats(var),tbl(:,cat),'OutputFormat','uniform');
Plot the number of categories for each categorical predictor.
figure barh(numCat); h = gca; h.YTickLabel = VarNames(cat); ylabel('Predictor') xlabel('Number of categories')
Train Model
For binary classification, the software uses a computational shortcut to find an optimal split for categorical predictors with many categories. For classification with more than two classes, you can choose an exact algorithm or a heuristic algorithm to find a good split by using the 'AlgorithmForCategorical' name-value pair argument of fitctree or templateTree. By default, the software selects the optimal subset of algorithms for each split using the known number of classes and levels of a categorical predictor.
Train a classification tree using tbl and Y. The response vector Y has two classes, so the software uses the exact algorithm for categorical predictor splits.
Mdl = fitctree(tbl,Y)
Mdl =
ClassificationTree
PredictorNames: {'age' 'workClass' 'fnlwgt' 'education' 'education_num' 'marital_status' 'occupation' 'relationship' 'race' 'sex' 'capital_gain' 'capital_loss' 'hours_per_week' 'native_country'}
ResponseName: 'Y'
CategoricalPredictors: [2 4 6 7 8 9 10 14]
ClassNames: [<=50K >50K]
ScoreTransform: 'none'
NumObservations: 32561
Properties, Methods
References
[1] Breiman, L., J. H. Friedman, R. A. Olshen, and C. J. Stone. Classification and Regression Trees. Boca Raton, FL: Chapman & Hall, 1984.
[2] Coppersmith, D., S. J. Hong, and J. R. M. Hosking. “Partitioning Nominal Attributes in Decision Trees.” Data Mining and Knowledge Discovery, Vol. 3, 1999, pp. 197–217.
See Also
fitctree | fitcensemble | templateTree | fitrtree