mvregress
Multivariate linear regression
Syntax
Description
beta = mvregress(X,Y)Y on
the design matrices in X.
beta = mvregress(X,Y,Name,Value)
Examples
Fit a multivariate regression model to panel data, assuming different intercepts and common slopes.
Load the sample data.
load fluThe dataset array flu contains national CDC flu estimates, and nine separate regional estimates based on Google® query data.
Extract the response and predictor data.
Y = double(flu(:,2:end-1)); [n,d] = size(Y); x = flu.WtdILI;
The responses in Y are the nine regional flu estimates. Observations exist for every week over a one-year period, so = 52. The dimension of the responses corresponds to the regions, so = 9. The predictors in x are the weekly national flu estimates.
Plot the flu data, grouped by region.
figure; regions = flu.Properties.VarNames(2:end-1); plot(x,Y,"x") legend(regions,Location="NorthWest")
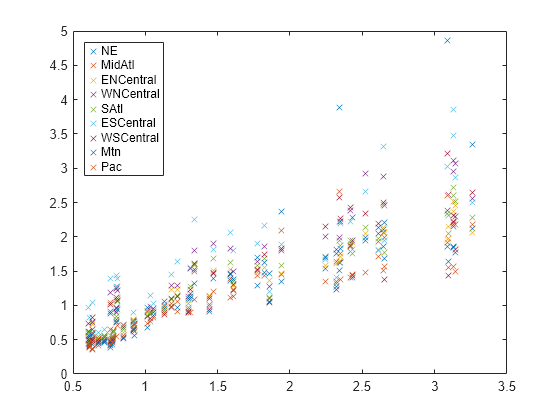
Fit the multivariate regression model , where and , with between-region concurrent correlation .
There are = 10 regression coefficients to estimate: nine intercept terms and a common slope. The input argument X should be an -element cell array of -by- design matrices.
X = cell(n,1); for i = 1:n X{i} = [eye(d) repmat(x(i),d,1)]; end [beta,Sigma] = mvregress(X,Y);
beta contains estimates of the -dimensional coefficient vector .
Sigma contains estimates of the -by- variance-covariance matrix , for the between-region concurrent correlations.
Plot the fitted regression model.
B = [beta(1:d)';repmat(beta(end),1,d)]; xx = linspace(.5,3.5)'; fits = [ones(size(xx)),xx]*B; figure; h = plot(x,Y,"x",xx,fits,"-"); for i = 1:d set(h(d+i),color=get(h(i),"color")); end legend(regions,Location="NorthWest");
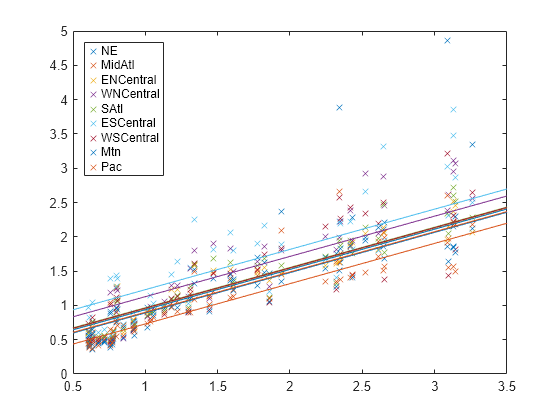
The plot shows that each regression line has a different intercept but the same slope. Upon visual inspection, some regression lines appear to fit the data better than others.
Fit a multivariate regression model to panel data using least squares, assuming different intercepts and slopes.
Load the sample data.
load flu;The dataset array flu contains national CDC flu estimates, and nine separate regional estimates based on Google® queries.
Save the response and predictor data as well as the size of the response variable.
Y = double(flu(:,2:end-1)); [n,d] = size(Y); x = flu.WtdILI;
The responses in Y are the nine regional flu estimates. Observations exist for every week over a one-year period, so = 52. The dimension of the responses corresponds to the regions, so = 9. The predictors in x are the weekly national flu estimates.
Fit the multivariate regression model , where and , with between-region concurrent correlation .
There are = 18 regression coefficients to estimate: nine intercept terms, and nine slope terms. X is an -element cell array of -by- design matrices.
X = cell(n,1); for i = 1:n X{i} = [eye(d) x(i)*eye(d)]; end [beta,Sigma] = mvregress(X,Y,'algorithm','cwls');
beta contains estimates of the -dimensional coefficient vector .
Plot the fitted regression model.
B = [beta(1:d)';beta(d+1:end)']; xx = linspace(.5,3.5)'; fits = [ones(size(xx)),xx]*B; figure; h = plot(x,Y,'x',xx,fits,'-'); for i = 1:d set(h(d+i),'color',get(h(i),'color')); end regions = flu.Properties.VarNames(2:end-1); legend(regions,'Location','NorthWest');
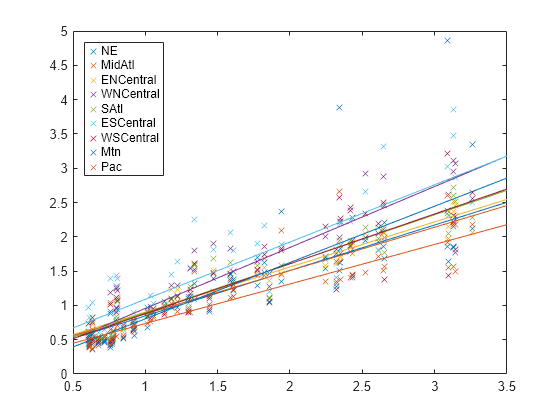
The plot shows that each regression line has a different intercept and slope.
Fit a multivariate regression model using a single -by- design matrix for all response dimensions.
Load the sample data.
load('flu')The dataset array flu contains national CDC flu estimates, and nine separate regional estimates based on Google® queries.
Extract the response and predictor data.
Y = double(flu(:,2:end-1)); [n,d] = size(Y); x = flu.WtdILI;
The responses in Y are the nine regional flu estimates. Observations exist for every week over a one-year period, so = 52. The dimension of the responses corresponds to the regions, so = 9. The predictors in x are the weekly national flu estimates.
Create an -by- design matrix X. Add a column of ones to include a constant term in the regression.
X = [ones(size(x)),x];
Fit the multivariate regression model
where and , with between-region concurrent correlation
There are 18 regression coefficients to estimate: nine intercept terms, and nine slope terms.
[beta,Sigma,E,CovB,logL] = mvregress(X,Y);
beta contains estimates of the -by- coefficient matrix. Sigma contains estimates of the -by- variance-covariance matrix for the between-region concurrent correlations. E is a matrix of the residuals. CovB is the estimated variance-covariance matrix of the regression coefficients. logL is the value of the log likelihood objective function after the last iteration.
Plot the fitted regression model.
B = beta; xx = linspace(.5,3.5)'; fits = [ones(size(xx)),xx]*B; figure h = plot(x,Y,'x', xx,fits,'-'); for i = 1:d set(h(d+i),'color',get(h(i),'color')) end regions = flu.Properties.VarNames(2:end-1); legend(regions,'Location','NorthWest')
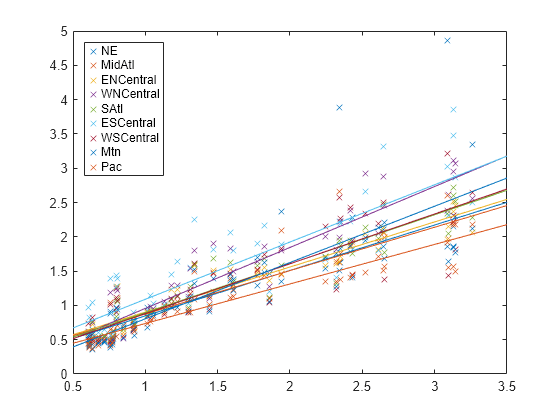
The plot shows that each regression line has a different intercept and slope.
Input Arguments
Design matrices for the multivariate regression, specified as
a matrix or cell array of matrices. n is the number
of observations in the data, K is the number of
regression coefficients to estimate, p is the number
of predictor variables, and d is the number of
dimensions in the response variable matrix Y.
If d = 1, then specify
Xas a single n-by-K design matrix.If d > 1 and all d dimensions have the same design matrix, then you can specify
Xas a single n-by-p design matrix (not in a cell array).If d > 1 and all n observations have the same design matrix, then you can specify
Xas a cell array containing a single d-by-K design matrix.If d > 1 and all n observations do not have the same design matrix, then specify
Xas a cell array of length n containing d-by-K design matrices.
To include a constant term in the regression model, each design matrix should contain a column of ones.
mvregress treats NaN values
in X as missing values, and ignores rows in X with
missing values.
Data Types: single | double | cell
Response variables, specified as an n-by-d matrix. n is
the number of observations in the data, and d is
the number of dimensions in the response. When d =
1, mvregress treats the values in Y like n independent
response values.
mvregress treats NaN values
in Y as missing values, and handles them according
to the estimation algorithm specified using the name-value pair argument algorithm.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'algorithm','cwls','covar0',C specifies
covariance-weighted least squares estimation using the covariance
matrix C.
Estimation algorithm, specified as the comma-separated pair
consisting of 'algorithm' and one of the following.
'mvn' | Ordinary multivariate normal maximum likelihood estimation. |
'ecm' | Maximum likelihood estimation via the ECM algorithm. |
'cwls' | Covariance-weighted least squares estimation. |
The default algorithm depends on the presence of missing data.
For complete data, the default is
'mvn'.If there are any missing responses (indicated by
NaN), the default is'ecm', provided the sample size is sufficient to estimate all parameters. Otherwise, the default algorithm is'cwls'.
Note
If algorithm has the value 'mvn',
then mvregress removes observations with missing
response values before estimation.
Example: 'algorithm','ecm'
Initial estimates for the regression coefficients, specified
as the comma-separated pair consisting of 'beta0' and
a vector with K elements. The default value is
a vector of 0s.
The beta0 argument is not used if the estimation algorithm is 'mvn'.
Initial estimate for the variance-covariance matrix, Sigma,
specified as the comma-separated pair consisting of 'covar0' and
a symmetric, positive definite, d-by-d matrix.
The default value is the identity matrix.
If the estimation algorithm is 'cwls',
then mvregress uses covar0 as
the weighting matrix at each iteration, without changing it.
Type of variance-covariance matrix to estimate for Y,
specified as the comma-separated pair consisting of 'covtype' and
one of the following.
'full' | Estimate all d(d + 1)/2 variance-covariance elements. |
'diagonal' | Estimate only the d diagonal elements of the variance-covariance matrix. |
Example: 'covtype','diagonal'
Maximum number of iterations for the estimation algorithm, specified
as the comma-separated pair consisting of 'maxiter' and
a positive integer.
Iterations continue until estimates are within the convergence
tolerances tolbeta and tolobj,
or the maximum number of iterations specified by maxiter is
reached. If both tolbeta and tolobj are
0, then mvregress performs maxiter iterations
with no convergence tests.
Example: 'maxiter',50
Function to evaluate at each iteration, specified as the comma-separated
pair consisting of 'outputfcn' and a function handle.
The function must return a logical true or false.
At each iteration, mvregress evaluates the function.
If the result is true, iterations stop. Otherwise,
iterations continue. For example, you could specify a function that
plots or displays current iteration results, and returns true if
you close the figure.
The function must accept three input arguments, in this order:
Vector of current coefficient estimates
Structure containing these three fields:
CovarCurrent value of the variance-covariance matrix iterationCurrent iteration number fvalCurrent value of the loglikelihood objective function Text that takes these three values:
'init'When the function is called during initialization 'iter'When the function is called after an iteration 'done'When the function is called after completion
Convergence tolerance for regression coefficients, specified
as the comma-separated pair consisting of 'tolbeta' and
a positive scalar value.
Let denote the estimate of the coefficient
vector at iteration t, and be the tolerance specified by tolbeta.
The convergence criterion for regression coefficient estimation is
where K is the length of and is the norm of a vector
Iterations continue until estimates are within the convergence
tolerances tolbeta and tolobj,
or the maximum number of iterations specified by maxiter is
reached. If both tolbeta and tolobj are
0, then mvregress performs maxiter iterations
with no convergence tests.
Example: 'tolbeta',1e-5
Convergence tolerance for the loglikelihood objective function,
specified as the comma-separated pair consisting of 'tolobj' and
a positive scalar value.
Let denote the value of the loglikelihood
objective function at iteration t, and be the tolerance specified by tolobj.
The convergence criterion for the objective function is
Iterations continue until estimates are within the convergence
tolerances tolbeta and tolobj,
or the maximum number of iterations specified by maxiter is
reached. If both tolbeta and tolobj are
0, then mvregress performs maxiter iterations
with no convergence tests.
Example: 'tolobj',1e-5
Format for the parameter estimate variance-covariance matrix, CovB,
specified as the comma-separated pair consisting of 'varformat' and
one of the following.
'beta' | Return the variance-covariance matrix for only the regression
coefficient estimates, beta. |
'full' | Return the variance-covariance matrix for both the regression
coefficient estimates, beta, and the variance-covariance
matrix estimate, Sigma. |
Example: 'varformat','full'
Type of variance-covariance matrix for parameter estimates,
specified as the comma-separated pair consisting of 'vartype' and
either 'hessian' or 'fisher'.
If the value is
'hessian', thenmvregressuses the Hessian, or observed information, matrix to computeCovB.If the value is
'fisher', thenmvregressuses the complete-data Fisher, or expected information, matrix to computeCovB.
The 'hessian' method takes into account the
increase uncertainties due to missing data, while the 'fisher' method
does not.
Example: 'vartype','fisher'
Output Arguments
Estimated regression coefficients, returned as a column vector or matrix.
If you specify
Xas a single n-by-K design matrix, thenmvregressreturnsbetaas a column vector of length K. For example, ifXis a 20-by-5 design matrix, thenbetais a 5-by-1 column vector.If you specify
Xas a cell array containing one or more d-by-K design matrices, thenmvregressreturnsbetaas a column vector of length K. For example, ifXis a cell array containing 2-by-10 design matrices, thenbetais a 10-by-1 column vector.If you specify
Xas a single n-by-p design matrix (not in a cell array), andYhas dimension d > 1, thenmvregressreturnsbetaas a p-by-d matrix. For example, ifXis a 20-by-5 design matrix, andYhas two dimensions such that d = 2, thenbetais a 5-by-2 matrix, and the fittedYvalues areX×beta.
Residuals for the fitted regression model, returned as an n-by-d matrix.
If algorithm has the value 'ecm' or 'cwls',
then mvregress computes the residual values corresponding
to missing values in Y as the difference between
the conditionally
imputed values and the fitted values.
Note
If algorithm has the value 'mvn',
then mvregress removes observations with missing
response values before estimation.
Parameter estimate variance-covariance matrix, returned as a square matrix.
Loglikelihood objective function value after the last iteration, returned as a scalar value.
More About
Multivariate normal regression is the regression of a d-dimensional response on a design matrix of predictor variables, with normally distributed errors. The errors can be heteroscedastic and correlated.
The model is
where
is a d-dimensional vector of responses.
is a design matrix of predictor variables.
is vector or matrix of regression coefficients.
is a d-dimensional vector of error terms, with multivariate normal distribution
The expectation/conditional maximization ('ecm')
and covariance-weighted least squares ('cwls')
estimation algorithms include imputation of missing response values.
Let denote missing observations. The conditionally imputed values are the expected value of the missing observation given the observed data, .
The joint distribution of the missing and observed responses is a multivariate normal distribution,
Using properties of the multivariate normal distribution, the imputed conditional expectation is given by
Note
mvregress only imputes missing response values.
Observations with missing values in the design matrix are removed.
References
[1] Little, Roderick J. A., and Donald B. Rubin. Statistical Analysis with Missing Data. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 2002.
[2] Meng, Xiao-Li, and Donald B. Rubin. “Maximum Likelihood Estimation via the ECM Algorithm.” Biometrika. Vol. 80, No. 2, 1993, pp. 267–278.
[3] Sexton, Joe, and A. R. Swensen. “ECM Algorithms that Converge at the Rate of EM.” Biometrika. Vol. 87, No. 3, 2000, pp. 651–662.
[4] Dempster, A. P., N. M. Laird, and D. B. Rubin. “Maximum Likelihood from Incomplete Data via the EM Algorithm.” Journal of the Royal Statistical Society. Series B, Vol. 39, No. 1, 1977, pp. 1–37.
Version History
Introduced in R2006b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)