Multivariate General Linear Model
This example shows how to set up a multivariate general linear model for estimation using mvregress.
Load sample data.
This data contains measurements on a sample of 205 auto imports from 1985.
Here, model the bivariate response of city and highway MPG (columns 14 and 15).
For predictors, use wheel base (column 3), curb weight (column 7), and fuel type (column 18). The first two predictors are continuous, and for this example are centered and scaled. Fuel type is a categorical variable with two categories (11 and 20), so a dummy indicator variable is needed for the regression.
load('imports-85')
Y = X(:,14:15);
[n,d] = size(Y);
X1 = zscore(X(:,3));
X2 = zscore(X(:,7));
X3 = X(:,18)==20;
Xmat = [ones(n,1) X1 X2 X3];The variable X3 is coded to have value 1 for the fuel type 20, and value 0 otherwise.
For convenience, the three predictors (wheel base, curb weight, and fuel type indicator) are combined into one design matrix, with an added intercept term.
Set up design matrices.
Given these predictors, the multivariate general linear model for the bivariate MPG response is
where . There are regression coefficients in total.
Create a length cell array of 2-by-8 (d-by-K) matrices for use with mvregress. The ith matrix in the cell array is
Xcell = cell(1,n); for i = 1:n Xcell{i} = [kron([Xmat(i,:)],eye(d))]; end
Given this specification of the design matrices, the corresponding parameter vector is
Estimate regression coefficients.
Fit the model using maximum likelihood estimation.
[beta,sigma,E,V] = mvregress(Xcell,Y); beta
beta = 8×1
33.5476
38.5720
0.9723
0.3950
-6.3064
-6.3584
-9.2284
-8.6663
These coefficient estimates show:
The expected city and highway MPG for cars of average wheel base, curb weight, and fuel type 11 are
33.5and38.6, respectively. For fuel type 20, the expected city and highway MPG are33.5476 - 9.2284 = 24.3192and38.5720 - 8.6663 = 29.9057.An increase of one standard deviation in curb weight has almost the same effect on expected city and highway MPG. Given all else is equal, the expected MPG decreases by about
6.3with each one standard deviation increase in curb weight, for both city and highway MPG.For each one standard deviation increase in wheel base, the expected city MPG increases
0.972, while the expected highway MPG increases by only0.395, given all else is equal.
Compute standard errors.
The standard errors for the regression coefficients are the square root of the diagonal of the variance-covariance matrix, V.
se = sqrt(diag(V))
se = 8×1
0.7365
0.7599
0.3589
0.3702
0.3497
0.3608
0.7790
0.8037
Reshape coefficient matrix.
You can easily reshape the regression coefficients into the original 4-by-2 matrix.
B = reshape(beta,2,4)'
B = 4×2
33.5476 38.5720
0.9723 0.3950
-6.3064 -6.3584
-9.2284 -8.6663
Check model assumptions.
Under the model assumptions, should be independent, with a bivariate standard normal distribution. In this 2-D case, you can assess the validity of this assumption using a scatter plot.
z = E/chol(sigma); figure() plot(z(:,1),z(:,2),'.') title('Standardized Residuals') hold on % Overlay standard normal contours z1 = linspace(-5,5); z2 = linspace(-5,5); [zx,zy] = meshgrid(z1,z2); zgrid = [reshape(zx,100^2,1),reshape(zy,100^2,1)]; zn = reshape(mvnpdf(zgrid),100,100); [c,h] = contour(zx,zy,zn); clabel(c,h)
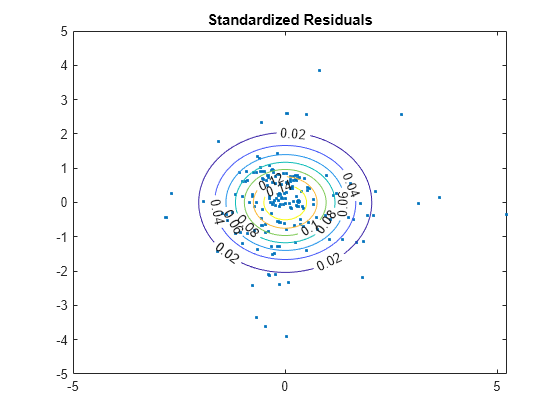
Several residuals are larger than expected, but overall, there is little evidence against the multivariate normality assumption.