updateMetrics
Update performance metrics in ECOC incremental learning classification model given new data
Since R2022a
Description
Given streaming data, updateMetrics measures the performance of
a configured multiclass error-correcting output codes (ECOC) classification model for
incremental learning (incrementalClassificationECOC object). updateMetrics stores the
performance metrics in the output model.
updateMetrics allows for flexible incremental learning. After you call
the function to update model performance metrics on an incoming chunk of data, you can perform
other actions before you train the model to the data. For example, you can decide whether you
need to train the model based on its performance on a chunk of data. Alternatively, you can
both update model performance metrics and train the model on the data as it arrives, in one
call, by using the updateMetricsAndFit
function.
To measure the model performance on a specified batch of data, call loss
instead.
Mdl = updateMetrics(Mdl,X,Y)Mdl, which is the input incremental learning model Mdl modified to contain the model performance metrics on the incoming
predictor and response data, X and Y
respectively.
When the input model is warm (Mdl.IsWarm is
true), updateMetrics overwrites previously computed
metrics, stored in the Metrics property, with the new values. Otherwise,
updateMetrics stores NaN values in
Metrics instead.
Examples
Train an ECOC classification model by using fitcecoc, convert it to an incremental learner, and then track its performance to streaming data.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1) % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Train ECOC Classification Model
Fit an ECOC classification model to a random sample of half the data.
idxtt = randsample([true false],n,true); TTMdl = fitcecoc(X(idxtt,:),Y(idxtt))
TTMdl =
ClassificationECOC
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Properties, Methods
TTMdl is a ClassificationECOC model object representing a traditionally trained model.
Convert Trained Model
Convert the traditionally trained classification model to a model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationECOC
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
IncrementalMdl is an incrementalClassificationECOC model. The model display shows that the model is warm (IsWarm is 1). Therefore, updateMetrics can track model performance metrics given data.
Track Performance Metrics
Track the model performance on the rest of the data by using the updateMetrics function. Simulate a data stream by processing 50 observations at a time. At each iteration:
Call
updateMetricsto update the cumulative and window classification error of the model given the incoming chunk of observations. Overwrite the previous incremental model to update theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model.Store the classification error and first model coefficient of the first binary learner .
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); mc = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = [IncrementalMdl.BinaryLearners{1}.Beta(1); zeros(nchunk+1,1)]; Xil = X(idxil,:); Yil = Y(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx)); mc{j,:} = IncrementalMdl.Metrics{"ClassificationError",:}; beta11(j+1) = IncrementalMdl.BinaryLearners{1}.Beta(1); end
IncrementalMdl is an incrementalClassificationECOC model object that has tracked the model performance to observations in the data stream.
Plot a trace plot of the performance metrics and estimated coefficient on separate tiles.
t = tiledlayout(2,1); nexttile plot(mc.Variables) xlim([0 nchunk]) ylabel("Classification Error") legend(mc.Properties.VariableNames) nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]); xlabel(t,"Iteration")

The cumulative loss is stable, whereas the window loss jumps throughout the training. does not change because updateMetrics does not fit the model to the data.
Train an ECOC classification model by using fitcecoc, convert it to an incremental learner, track its performance on streaming data, and then fit the model to the data. For incremental learning functions, orient the observations in columns, and specify observation weights.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1); % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Suppose that the data from a stationary subject (Y <= 2) has double the quality of the data from a moving subject. Create a weight variable that assigns a weight of 2 to observations from a stationary subject and 1 to a moving subject.
W = ones(n,1) + (Y <=2);
Train ECOC Classification Model
Fit an ECOC classification model to a random sample of half the data. Specify observation weights.
idxtt = randsample([true false],n,true); TTMdl = fitcecoc(X(idxtt,:),Y(idxtt),Weights=W(idxtt))
TTMdl =
ClassificationECOC
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Properties, Methods
TTMdl is a ClassificationECOC model object representing a traditionally trained ECOC classification model.
Convert Trained Model
Convert the traditionally trained model to a model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationECOC
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
IncrementalMdl is an incrementalClassificationECOC model. Because class names are specified in IncrementalMdl.ClassNames, labels encountered during incremental learning must be in IncrementalMdl.ClassNames.
Separately Track Performance Metrics and Fit Model
Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. For incremental learning, orient the observations of the predictor data in columns. At each iteration:
Simulate a data stream by processing 50 observations at a time.
Call
updateMetricsto update the cumulative and window classification error of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify that the observations are oriented in columns, and specify the observation weights.Store the classification error.
Call
fitto fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify that the observations are oriented in columns, and specify the observation weights.
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); mc = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); Xil = X(idxil,:)'; Yil = Y(idxil); Wil = W(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(:,idx),Yil(idx), ... Weights=Wil(idx),ObservationsIn="columns"); mc{j,:} = IncrementalMdl.Metrics{"ClassificationError",:}; IncrementalMdl = fit(IncrementalMdl,Xil(:,idx),Yil(idx), ... Weights=Wil(idx),ObservationsIn="columns"); end
IncrementalMdl is an incrementalClassificationECOC model object trained on all the data in the stream.
Alternatively, you can use updateMetricsAndFit to update performance metrics of the model given a new chunk of data, and then fit the model to the data.
Plot a trace plot of the performance metrics.
plot(mc.Variables) xlim([0 nchunk]) legend(mc.Properties.VariableNames) ylabel("Classification Error") xlabel("Iteration")

The cumulative loss gradually stabilizes, whereas the window loss jumps throughout the training.
Incrementally train an ECOC classification model only when its performance degrades.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Configure an ECOC classification model for incremental learning so that the maximum number of expected classes is 5, and the metrics window size is 1000. Prepare the model for updateMetrics by fitting the model to the first 1000 observations.
Mdl = incrementalClassificationECOC(MaxNumClasses=5,MetricsWindowSize=1000); initobs = 1000; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationECOC model object.
Determine whether the model is warm by querying the model property.
isWarm = Mdl.IsWarm
isWarm = logical
1
Mdl.IsWarm is 1; therefore, Mdl is warm.
Perform incremental learning, with conditional fitting, by following this procedure for each iteration:
Simulate a data stream by processing a chunk of 100 observations at a time.
Update the model performance on the incoming chunk of data.
Fit the model to the chunk of data only when the misclassification error rate is greater than 0.05.
When tracking performance and fitting, overwrite the previous incremental model.
Store the misclassification error rate and the first model coefficient of the first binary learner to see how they evolve during training.
Track when
fittrains the model.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); beta11 = zeros(nchunk,1); ce = array2table(nan(nchunk,2),VariableNames=["Cumulative","Window"]); trained = false(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; if ce{j,2} > 0.05 Mdl = fit(Mdl,X(idx,:),Y(idx)); trained(j) = true; end beta11(j) = Mdl.BinaryLearners{1}.Beta(1); end
Mdl is an incrementalClassificationECOC model object trained on all the data in the stream.
To see how the model performance and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(beta11) hold on plot(find(trained),beta11(trained),"r.") xlim([0 nchunk]) ylabel("\beta_{11}") legend("\beta_{11}","Training occurs",Location="best") hold off nexttile plot(ce.Variables) yline(0.05,"--") xlim([0 nchunk]) ylabel("Misclassification Error Rate") legend(ce.Properties.VariableNames,Location="best") xlabel(t,"Iteration")

The trace plot of shows periods of constant values, during which the loss within the previous observation window is at most 0.05.
Prepare an incremental ECOC learner by specifying the maximum number of classes. Configure the model to track its performance and the performance of each binary learner in the model.
Create an ECOC model for incremental learning by calling incrementalClassificationECOC. Specify a maximum of 5 expected classes in the data, and specify to update the performance metrics of binary learners in the model.
Mdl = incrementalClassificationECOC(MaxNumClasses=5,UpdateBinaryLearnerMetrics=true);
Mdl is an incrementalClassificationECOC model. All its properties are read-only.
Display the coding design matrix.
Mdl.CodingMatrix
ans = 5×10
1 1 1 1 0 0 0 0 0 0
-1 0 0 0 1 1 1 0 0 0
0 -1 0 0 -1 0 0 1 1 0
0 0 -1 0 0 -1 0 -1 0 1
0 0 0 -1 0 0 -1 0 -1 -1
Each row corresponds to a class, and each column corresponds to a binary learner. For example, the first binary learner is for classes 1 and 2, and the fourth binary learner is for classes 1 and 5, where both learners assume class 1 as a positive class.
Determine whether the model is warm by querying the model property.
isWarm = Mdl.IsWarm
isWarm = logical
0
Mdl.IsWarm is 0; therefore, Mdl is not warm.
Determine the number of observations that incremental fitting functions, such as fit, must process before measuring the performance of the model by displaying the size of the metrics warm-up period.
numObsBeforeMetrics = Mdl.MetricsWarmupPeriod
numObsBeforeMetrics = 1000
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
The response vector actid contains the activity IDs in integers: 1, 2, 3, 4, and 5 representing sitting, standing, walking, running, and dancing, respectively. For details on the data set, enter Description at the command line.
Implement incremental learning by performing the following actions at each iteration:
Simulate a data stream by processing a chunk of 50 observations.
Measure model performance metrics on the incoming chunk using
updateMetrics, and overwrite the input model.Fit the model to the incoming chunk, and overwrite the input model.
Store the first model coefficient of the first binary learner .
Store the misclassification error rates for the model and its binary learners.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = zeros(nchunk,1); numBinaryLearners = length(Mdl.BinaryLearners); BinaryLearnerIsWarm = zeros(numBinaryLearners,1); numtrainobs = zeros(nchunk,numBinaryLearners); blMetrics = cell(numBinaryLearners,1); for k = 1:numBinaryLearners blMetrics{k} = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); end % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; for k = 1:numBinaryLearners blMetrics{k}{j,:} = Mdl.BinaryLearners{k}.Metrics{"ClassificationError",:}; end Mdl = fit(Mdl,X(idx,:),Y(idx)); beta11(j) = Mdl.BinaryLearners{1}.Beta(1); for k = 1:numBinaryLearners numtrainobs(j,k) = Mdl.BinaryLearners{k}.NumTrainingObservations; if Mdl.BinaryLearners{k}.IsWarm == false BinaryLearnerIsWarm(k) = j; end end end
Mdl is an incrementalClassificationECOC model object trained on all the data in the stream.
To see how the performance metrics and evolve during incremental learning, plot them on separate tiles.
figure t = tiledlayout(2,1); nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]) nexttile plot(ce.Variables) ylabel("ClassificationError") xline(numObsBeforeMetrics/numObsPerChunk,"--") xlim([0 nchunk]) legend(ce.Properties.VariableNames) xlabel(t,"Iteration")

mdlIsWarm = numObsBeforeMetrics/numObsPerChunk
mdlIsWarm = 20
The plot suggests that fit always fits the model to the data, and updateMetrics does not track the classification error until after the metrics warm-up period (20 chunks).
Plot the performance metrics of the binary learners for class 3.
bl = find(Mdl.CodingMatrix(3,:)); % Find binary learners for class 3 figure t = tiledlayout(length(bl),1); ax = zeros(length(bl),1); for i = 1 : length(bl) ax(i) = nexttile; plot(blMetrics{bl(i)}.Variables) xline(numObsBeforeMetrics/numObsPerChunk,"--") xline(BinaryLearnerIsWarm(1),":") xlim([0 nchunk]) positiveClass = find(Mdl.CodingMatrix(:,bl(i))==1); negativeClass = find(Mdl.CodingMatrix(:,bl(i))==-1); title(join(["Binary Learner for classes ",positiveClass," and ",negativeClass])) end legend(ax(1),blMetrics{bl(1)}.Properties.VariableNames,Location="best") linkaxes(ax) ylim([0,0.02]) ylabel(t,"ClassificationError") xlabel(t,"Iteration")
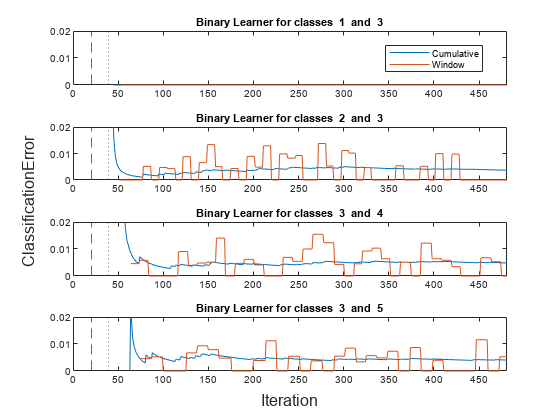
BinaryLearnerIsWarm(bl)
ans = 4×1
42
41
51
60
A binary learner becomes warm after the software fits the learner to 1000 observations. Because each binary learner uses only the observations corresponding to its positive or negative classes, binary learners become warm at different learning iterations. Also, updateMetrics updates the Window metrics for the binary learners asynchronously.
The first plot shows that the classification error (or misclassification rate) is 0 for the binary learner that determines an activity between sitting (class 1) and walking (class 3). The next three plots show the misclassification rates for the three binary learners that distinguish walking (class 3) from standing (class 2), running (class 4), and dancing (class 5), respectively. These three binary learners have higher misclassification rates than the first binary learner.
Input Arguments
Incremental learning model whose performance is measured, specified as an incrementalClassificationECOC model object. You can create
Mdl by calling incrementalClassificationECOC
directly, or by converting a supported, traditionally trained machine learning model
using the incrementalLearner function.
If Mdl.IsWarm is false,
updateMetrics does not track the performance of the model. Before
updateMetrics can track performance metrics, you must perform both
of these actions:
Fit the input model
Mdlto all expected classes (see theMaxNumClassesandClassNamesarguments ofincrementalClassificationECOC).Fit the input model
MdltoMdl.MetricsWarmupPeriodobservations by passingMdland the data tofit. For more details, see Performance Metrics.
Chunk of predictor data, specified as a floating-point matrix of n
observations and Mdl.NumPredictors predictor
variables. The value of the ObservationsIn name-value
argument determines the orientation of the variables and observations. The default
ObservationsIn value is "rows", which indicates that
observations in the predictor data are oriented along the rows of
X.
The length of the observation labels Y and the number of observations in X must be equal; Y( is the label of observation j (row or column) in j)X.
Note
If
Mdl.NumPredictors= 0,updateMetricsinfers the number of predictors fromX, and sets the corresponding property of the output model. Otherwise, if the number of predictor variables in the streaming data changes fromMdl.NumPredictors,updateMetricsissues an error.updateMetricssupports only floating-point input predictor data. If your input data includes categorical data, you must prepare an encoded version of the categorical data. Usedummyvarto convert each categorical variable to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Chunk of labels, specified as a categorical, character, or string array, a logical or floating-point vector, or a cell array of character vectors.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row or column) in j)X.
updateMetrics issues an error when one or both of these conditions
are met:
Ycontains a new label and the maximum number of classes has already been reached (see theMaxNumClassesandClassNamesarguments ofincrementalClassificationECOC).The
ClassNamesproperty of the input modelMdlis nonempty, and the data types ofYandMdl.ClassNamesare different.
Data Types: char | string | cell | categorical | logical | single | double
Note
If an observation (predictor or label) or weight contains at
least one missing (NaN) value, updateMetrics ignores the
observation. Consequently, updateMetrics uses fewer than n
observations to compute the model performance, where n is the number of
observations in X.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: ObservationsIn="columns",Weights=W specifies that the columns
of the predictor matrix correspond to observations, and the vector W
contains observation weights to apply during incremental learning.
Predictor data observation dimension, specified as "rows" or
"columns".
Example: ObservationsIn="columns"
Data Types: char | string
Chunk of observation weights, specified as a floating-point vector of positive values.
updateMetrics weighs the observations in X
with the corresponding values in Weights. The size of
Weights must equal n, which is the number of
observations in X.
By default, Weights is ones(.n,1)
For more details, including normalization schemes, see Observation Weights.
Example: Weights=W specifies the observation weights as the vector
W.
Data Types: double | single
Output Arguments
Updated ECOC classification model for incremental learning, returned as an
incremental learning model object of the same data type as the input model
Mdl, an incrementalClassificationECOC object.
If the model is not warm, updateMetrics does
not compute performance metrics. As a result, the Metrics property of
Mdl remains completely composed of NaN values. If the
model is warm, updateMetrics computes the cumulative and window performance
metrics on the new data X and Y, and overwrites the
corresponding elements of Mdl.Metrics. All other properties of the input
model Mdl carry over to the output model Mdl. For more details, see
Performance Metrics.
Tips
Unlike traditional training, incremental learning might not have a separate test (holdout) set. Therefore, to treat each incoming chunk of data as a test set, pass the incremental model and each incoming chunk to
updateMetricsbefore training the model on the same data usingfit.
Algorithms
updateMetricsandupdateMetricsAndFittrack model performance metrics, specified by the row labels of the table inMdl.Metrics, from new data only when the incremental model is warm (IsWarmproperty istrue).If you create an incremental model by using
incrementalLearnerandMetricsWarmupPeriodis 0 (default forincrementalLearner), the model is warm at creation.Otherwise, an incremental model becomes warm after the
fitorupdateMetricsAndFitfunction performs both of these actions:Fit the incremental model to
Mdl.MetricsWarmupPeriodobservations, which is the metrics warm-up period.Fit the incremental model to all expected classes (see the
MaxNumClassesandClassNamesarguments ofincrementalClassificationECOC).
The
Mdl.Metricsproperty stores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsandupdateMetricsAndFitupdate the metrics at the following frequencies:Cumulative— The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.Window— The functions compute metrics based on all observations within a window determined by theMdl.MetricsWindowSizeproperty.Mdl.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMdl.MetricsWindowSizeis 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
Mdl.MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is filled, overwrite
Mdl.Metrics.Windowwith the weighted average performance in the metrics window. If the buffer is overfilled when the function processes a batch of observations, the latest incomingMdl.MetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMdl.MetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the function uses the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNscore when computing theCumulativeandWindowperformance metric values.
If the prior class probability distribution is known (in other words, the prior distribution is not empirical), updateMetrics normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that the default observation weights are the respective prior class probabilities.
If the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call updateMetrics.
Extended Capabilities
Usage notes and limitations:
Use
saveLearnerForCoder,loadLearnerForCoder, andcodegen(MATLAB Coder) to generate code for theupdateMetricsfunction. Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls theupdateMetricsfunction. Then usecodegento generate code for the entry-point function.To generate single-precision C/C++ code for
updateMetrics, specifyDataType="single"when you call theloadLearnerForCoderfunction.This table contains notes about the arguments of
updateMetrics. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlFor usage notes and limitations of the model object, see
incrementalClassificationECOC.XBatch-to-batch, the number of observations can be a variable size, but must equal the number of observations in
Y.The number of predictor variables must equal
Mdl.NumPredictors.Xmust besingleordouble.
YBatch-to-batch, the number of observations can be a variable size, but must equal the number of observations in
X.For classification problems, all labels in
Ymust be included inMdl.ClassNames.YandMdl.ClassNamesmust have the same data type.
The following restrictions apply:
Use a homogeneous data type for all floating-point input arguments and object properties, specifically, either
singleordouble.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2022a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)