fitcnet
Syntax
Description
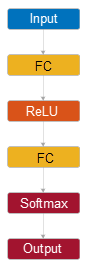
Use fitcnet to train a neural network for classification,
such as a feedforward, fully connected network. In a feedforward, fully connected network,
the first fully connected layer has a connection from the network input (predictor data), and
each subsequent layer has a connection from the previous layer. Each fully connected layer
multiplies the input by a weight matrix and then adds a bias vector. An activation function
follows each fully connected layer. The final fully connected layer and the subsequent softmax
activation function produce the network's output, namely classification scores (posterior
probabilities) and predicted labels. For more information, see Neural Network Structure.
Mdl = fitcnet(Tbl,ResponseVarName)Mdl trained using the
predictors in the table Tbl and the class labels in the
ResponseVarName table variable.
Mdl = fitcnet(___,Name=Value)LayerSizes and Activations name-value
arguments.
[
also returns Mdl,AggregateOptimizationResults] = fitcnet(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments. You must
also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this syntax to
optimize on compact model size instead of cross-validation loss, and to perform a set of
multiple optimization problems that have the same options but different constraint
bounds.
Examples
Train a neural network classifier, and assess the performance of the classifier on a test set.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the partition c = cvpartition(creditrating.Rating,"Holdout",0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set creditTrain = creditrating(trainingIndices,:); creditTest = creditrating(testIndices,:);
Train a neural network classifier by passing the training data creditTrain to the fitcnet function.
Mdl = fitcnet(creditTrain,"Rating")Mdl =
ClassificationNeuralNetwork
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
CategoricalPredictors: 6
ClassNames: [AAA AA A BBB BB B CCC]
ScoreTransform: 'none'
NumObservations: 3146
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Mdl is a trained ClassificationNeuralNetwork classifier. You can use dot notation to access the properties of Mdl. For example, you can specify Mdl.TrainingHistory to get more information about the training history of the neural network model.
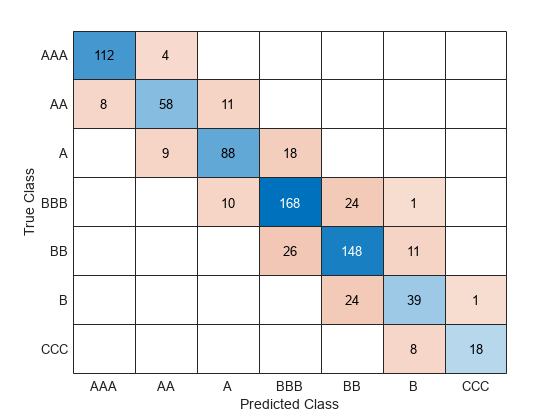
Evaluate the performance of the classifier on the test set by computing the test set classification error. Visualize the results by using a confusion matrix.
testAccuracy = 1 - loss(Mdl,creditTest,"Rating", ... "LossFun","classiferror")
testAccuracy = 0.7977
confusionchart(creditTest.Rating,predict(Mdl,creditTest))
Configure the fully connected layers of the neural network.
Load the ionosphere data set, which includes radar signal data. X contains the predictor data, and Y is the response variable, whose values represent either good ("g") or bad ("b") radar signals.
load ionosphereSeparate the data into training data (XTrain and YTrain) and test data (XTest and YTest) by using a stratified holdout partition. Reserve approximately 30% of the observations for testing, and use the rest of the observations for training.
rng("default") % For reproducibility of the partition cvp = cvpartition(Y,"Holdout",0.3); XTrain = X(training(cvp),:); YTrain = Y(training(cvp)); XTest = X(test(cvp),:); YTest = Y(test(cvp));
Train a neural network classifier. Specify to have 35 outputs in the first fully connected layer and 20 outputs in the second fully connected layer. By default, both layers use a rectified linear unit (ReLU) activation function. You can change the activation functions for the fully connected layers by using the Activations name-value argument.
Mdl = fitcnet(XTrain,YTrain, ... "LayerSizes",[35 20])
Mdl =
ClassificationNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 246
LayerSizes: [35 20]
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [47×7 table]
Properties, Methods
Access the weights and biases for the fully connected layers of the trained classifier by using the LayerWeights and LayerBiases properties of Mdl. The first two elements of each property correspond to the values for the first two fully connected layers, and the third element corresponds to the values for the final fully connected layer with a softmax activation function for classification. For example, display the weights and biases for the second fully connected layer.
Mdl.LayerWeights{2}ans = 20×35
0.0481 0.2501 -0.1535 -0.0934 0.0760 -0.0579 -0.2465 1.0411 0.3712 -1.2007 1.1162 0.4296 0.4045 0.5005 0.8839 0.4624 -0.3154 0.3454 -0.0487 0.2648 0.0732 0.5773 0.4286 0.0881 0.9468 0.2981 0.5534 1.0518 -0.0224 0.6894 0.5527 0.7045 -0.6124 0.2145 -0.0790
-0.9489 -1.8343 0.5510 -0.5751 -0.8726 0.8815 0.0203 -1.6379 2.0315 1.7599 -1.4153 -1.4335 -1.1638 -0.1715 1.1439 -0.7661 1.1230 -1.1982 -0.5409 -0.5821 -0.0627 -0.7038 -0.0817 -1.5773 -1.4671 0.2053 -0.7931 -1.6201 -0.1737 -0.7762 -0.3063 -0.8771 1.5134 -0.4611 -0.0649
-0.1910 0.0246 -0.3511 0.0097 0.3160 -0.0693 0.2270 -0.0783 -0.1626 -0.3478 0.2765 0.4179 0.0727 -0.0314 -0.1798 -0.0583 0.1375 -0.1876 0.2518 0.2137 0.1497 0.0395 0.2859 -0.0905 0.4325 -0.2012 0.0388 -0.1441 -0.1431 -0.0249 -0.2200 0.0860 -0.2076 0.0132 0.1737
-0.0415 -0.0059 -0.0753 -0.1477 -0.1621 -0.1762 0.2164 0.1710 -0.0610 -0.1402 0.1452 0.2890 0.2872 -0.2616 -0.4204 -0.2831 -0.1901 0.0036 0.0781 -0.0826 0.1588 -0.2782 0.2510 -0.1069 -0.2692 0.2306 0.2521 0.0306 0.2524 -0.4218 0.2478 0.2343 -0.1031 0.1037 0.1598
1.1848 1.6142 -0.1352 0.5774 0.5491 0.0103 0.0209 0.7219 -0.8643 -0.5578 1.3595 1.5385 1.0015 0.7416 -0.4342 0.2279 0.5667 1.1589 0.7100 0.1823 0.4171 0.7051 0.0794 1.3267 1.2659 0.3197 0.3947 0.3436 -0.1415 0.6607 1.0071 0.7726 -0.2840 0.8801 0.0848
0.2486 -0.2920 -0.0004 0.2806 0.2987 -0.2709 0.1473 -0.2580 -0.0499 -0.0755 0.2000 0.1535 -0.0285 -0.0520 -0.2523 -0.2505 -0.0437 -0.2323 0.2023 0.2061 -0.1365 0.0744 0.0344 -0.2891 0.2341 -0.1556 0.1459 0.2533 -0.0583 0.0243 -0.2949 -0.1530 0.1546 -0.0340 -0.1562
-0.0516 0.0640 0.1824 -0.0675 -0.2065 -0.0052 -0.1682 -0.1520 0.0060 0.0450 0.0813 -0.0234 0.0657 0.3219 -0.1871 0.0658 -0.2103 0.0060 -0.2831 -0.1811 -0.0988 0.2378 -0.0761 0.1714 -0.1596 -0.0011 0.0609 0.4003 0.3687 -0.2879 0.0910 0.0604 -0.2222 -0.2735 -0.1155
-0.6192 -0.7804 -0.0506 -0.4205 -0.2584 -0.2020 -0.0008 0.0534 1.0185 -0.0307 -0.0539 -0.2020 0.0368 -0.1847 0.0886 -0.4086 -0.4648 -0.3785 0.1542 -0.5176 -0.3207 0.1893 -0.0313 -0.5297 -0.1261 -0.2749 -0.6152 -0.5914 -0.3089 0.2432 -0.3955 -0.1711 0.1710 -0.4477 0.0718
0.5049 -0.1362 -0.2218 0.1637 -0.1282 -0.1008 0.1445 0.4527 -0.4887 0.0503 0.1453 0.1316 -0.3311 -0.1081 -0.7699 0.4062 -0.1105 -0.0855 0.0630 -0.1469 -0.2533 0.3976 0.0418 0.5294 0.3982 0.1027 -0.0973 -0.1282 0.2491 0.0425 0.0533 0.1578 -0.8403 -0.0535 -0.0048
1.1109 -0.0466 0.4044 0.6366 0.1863 0.5660 0.2839 0.8793 -0.5497 0.0057 0.3468 0.0980 0.3364 0.4669 0.1466 0.7883 -0.1743 0.4444 0.4535 0.1521 0.7476 0.2246 0.4473 0.2829 0.8881 0.4666 0.6334 0.3105 0.9571 0.2808 0.6483 0.1180 -0.4558 1.2486 0.2453
-1.8572 -2.6653 -0.2140 -0.3477 -0.8055 0.9079 0.6366 -1.3961 1.7287 0.7673 -1.8550 -1.7492 -1.3679 -0.3315 2.7078 -0.7556 0.0769 -1.5157 -0.4442 -0.6340 0.2048 -1.0457 -0.1914 -1.6244 -1.7866 -0.6572 -1.8200 -1.3674 -0.6874 -1.1299 -0.0000 -1.9709 0.7340 -0.4415 -0.3320
0.2370 0.8540 -0.7814 -0.2181 -0.0569 0.0027 -0.2945 0.1143 -0.6404 -0.4251 0.5823 0.5555 0.4856 0.1239 0.3043 0.1653 -0.2534 0.0117 0.3500 -0.0883 0.4188 0.1499 0.2924 1.0637 0.7403 0.0144 -0.5028 0.9141 -0.1405 -0.3842 0.6864 -0.0071 -0.1437 0.2459 -0.1786
-0.4045 -1.0484 -0.1285 -0.4945 -0.3934 -0.0459 -0.2790 -0.0375 1.5520 -0.5361 0.3359 -0.5839 -0.4385 -0.6225 -1.1123 -0.5139 0.9128 -0.4074 -0.3080 -1.1164 -0.5790 -0.0578 -0.7154 -0.5121 -0.3480 0.3290 -0.2253 0.1340 -0.4615 0.1242 -0.8776 0.3386 -0.0865 -0.2834 0.0347
0.0617 -0.1042 -0.1774 -0.0899 -0.0925 -0.3826 -0.0153 0.1875 0.1134 -0.0190 -0.1245 0.0485 -0.1353 0.0801 -0.6564 -0.2706 -0.3851 -0.0657 -0.0888 -0.3534 -0.0382 -0.1895 -0.1363 -0.4116 -0.2031 -0.1712 -0.1507 -0.1233 -0.3996 -0.0849 -0.2433 -0.1504 -0.1387 -0.1659 0.0534
0.2469 0.8184 -0.7969 0.3706 0.0860 0.6381 -0.3027 0.5547 0.0410 -0.5412 1.4578 1.1429 0.6856 0.3181 0.8661 0.4728 -0.0410 0.8727 0.3093 0.6220 0.2403 0.1572 0.4424 0.4320 0.3807 -0.0664 0.5451 1.1958 -0.0054 -0.0761 0.6085 0.5600 0.2312 0.8952 0.3766
⋮
Mdl.LayerBiases{2}ans = 20×1
0.6147
0.1891
-0.2767
-0.2977
1.3655
0.0347
0.1509
-0.4839
-0.3960
0.9248
-0.5636
0.1190
-0.5285
-0.3493
1.7387
⋮
The final fully connected layer has two outputs, one for each class in the response variable. The number of layer outputs corresponds to the first dimension of the layer weights and layer biases.
size(Mdl.LayerWeights{end})ans = 1×2
2 20
size(Mdl.LayerBiases{end})ans = 1×2
2 1
To estimate the performance of the trained classifier, compute the test set classification error for Mdl.
testError = loss(Mdl,XTest,YTest, ... "LossFun","classiferror")
testError = 0.0774
accuracy = 1 - testError
accuracy = 0.9226
Mdl accurately classifies approximately 92% of the observations in the test set.
Since R2025a
Specify a custom neural network architecture using Deep Learning Toolbox™.
Load the ionosphere data set, which includes radar signal data. X contains the predictor data, and Y is the response variable, whose values represent either good ("g") or bad ("b") radar signals.
load ionosphereSeparate the data into training data (XTrain and YTrain) and test data (XTest and YTest) by using a stratified holdout partition. Reserve approximately 30% of the observations for testing, and use the rest of the observations for training.
rng("default") % For reproducibility of the partition cvp = cvpartition(Y,Holdout=0.3); XTrain = X(training(cvp),:); YTrain = Y(training(cvp)); XTest = X(test(cvp),:); YTest = Y(test(cvp));
Define a neural network architecture with these characteristics:
A feature input layer with an input size that matches the number of predictors.
Three fully connected layers followed by leaky ReLU layers, connected in series, where the fully connected layers have output sizes of 16, and addition layers after the second and third fully connected layers.
Skip connections around the second and third fully connected layers using the addition layers.
A final fully connected layer with an output size that matches the number of classes followed by a softmax layer.
inputSize = size(XTrain,2);
outputSize = numel(unique(YTrain));
net = dlnetwork;
layers = [
featureInputLayer(inputSize)
fullyConnectedLayer(30)
leakyReluLayer(Name="lrelu1")
fullyConnectedLayer(30)
additionLayer(2,Name="add2")
leakyReluLayer(Name="lrelu2")
fullyConnectedLayer(30)
additionLayer(2,Name="add3")
leakyReluLayer
fullyConnectedLayer(outputSize)
softmaxLayer];
net = addLayers(net,layers);
net = connectLayers(net,"lrelu1","add2/in2");
net = connectLayers(net,"lrelu2","add3/in2");Visualize the neural network architecture in a plot.
figure plot(net)
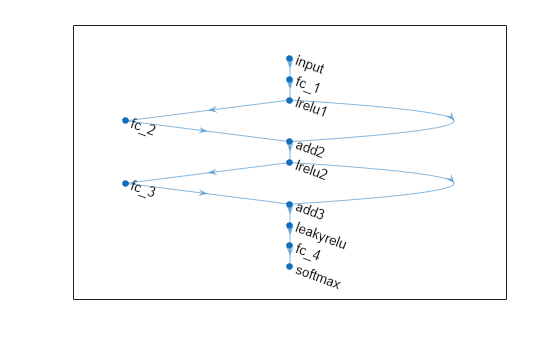
Train a neural network classifier.
Mdl = fitcnet(XTrain,YTrain,Network=net,Standardize=true)
Mdl =
ClassificationNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 246
LayerSizes: []
Activations: ''
OutputLayerActivation: ''
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [30×5 table]
View network information using dlnetwork.
Properties, Methods
To estimate the performance of the trained classifier, compute the test set classification error.
testError = loss(Mdl,XTest,YTest, ... LossFun="classiferror")
testError = 0.0774
At each iteration of the training process, compute the validation loss of the neural network. Stop the training process early if the validation loss reaches a reasonable minimum.
Load the patients data set. Create a table from the data set. Each row corresponds to one patient, and each column corresponds to a diagnostic variable. Use the Smoker variable as the response variable, and the rest of the variables as predictors.
load patients
tbl = table(Diastolic,Systolic,Gender,Height,Weight,Age,Smoker);Separate the data into a training set tblTrain and a validation set tblValidation by using a stratified holdout partition. The software reserves approximately 30% of the observations for the validation data set and uses the rest of the observations for the training data set.
rng("default") % For reproducibility of the partition c = cvpartition(tbl.Smoker,"Holdout",0.30); trainingIndices = training(c); validationIndices = test(c); tblTrain = tbl(trainingIndices,:); tblValidation = tbl(validationIndices,:);
Train a neural network classifier by using the training set. Specify the Smoker column of tblTrain as the response variable. Evaluate the model at each iteration by using the validation set. Specify to display the training information at each iteration by using the Verbose name-value argument. By default, the training process ends early if the validation cross-entropy loss is greater than or equal to the minimum validation cross-entropy loss computed so far, six times in a row. To change the number of times the validation loss is allowed to be greater than or equal to the minimum, specify the ValidationPatience name-value argument.
Mdl = fitcnet(tblTrain,"Smoker", ... "ValidationData",tblValidation, ... "Verbose",1);
|==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 1| 2.602935| 26.866935| 0.262009| 0.042297| 2.793048| 0| | 2| 1.470816| 42.594723| 0.058323| 0.006401| 1.247046| 0| | 3| 1.299292| 25.854432| 0.034910| 0.002804| 1.507857| 1| | 4| 0.710465| 11.629107| 0.013616| 0.005081| 0.889157| 0| | 5| 0.647783| 2.561740| 0.005753| 0.011369| 0.766728| 0| | 6| 0.645541| 0.681579| 0.001000| 0.001134| 0.776072| 1| | 7| 0.639611| 1.544692| 0.007013| 0.001821| 0.776320| 2| | 8| 0.604189| 5.045676| 0.064190| 0.000490| 0.744919| 0| | 9| 0.565364| 5.851552| 0.068845| 0.000544| 0.694226| 0| | 10| 0.391994| 8.377717| 0.560480| 0.000547| 0.425466| 0| |==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 11| 0.383843| 0.630246| 0.110270| 0.001333| 0.428487| 1| | 12| 0.369289| 2.404750| 0.084395| 0.000723| 0.405728| 0| | 13| 0.357839| 6.220679| 0.199197| 0.000646| 0.378480| 0| | 14| 0.344974| 2.752717| 0.029013| 0.000953| 0.367279| 0| | 15| 0.333747| 0.711398| 0.074513| 0.002158| 0.348499| 0| | 16| 0.327763| 0.804818| 0.122178| 0.000678| 0.330237| 0| | 17| 0.327702| 0.778169| 0.009810| 0.000758| 0.329095| 0| | 18| 0.327277| 0.020615| 0.004377| 0.000499| 0.329141| 1| | 19| 0.327273| 0.010018| 0.003313| 0.000544| 0.328773| 0| | 20| 0.327268| 0.019497| 0.000805| 0.000914| 0.328831| 1| |==========================================================================================| | Iteration | Train Loss | Gradient | Step | Iteration | Validation | Validation | | | | | | Time (sec) | Loss | Checks | |==========================================================================================| | 21| 0.327228| 0.113983| 0.005397| 0.000540| 0.329085| 2| | 22| 0.327138| 0.240166| 0.012159| 0.000522| 0.329406| 3| | 23| 0.326865| 0.428912| 0.036841| 0.000646| 0.329952| 4| | 24| 0.325797| 0.255227| 0.139585| 0.000505| 0.331246| 5| | 25| 0.325181| 0.758050| 0.135868| 0.001399| 0.332035| 6| |==========================================================================================|
Create a plot that compares the training cross-entropy loss and the validation cross-entropy loss at each iteration. By default, fitcnet stores the loss information inside the TrainingHistory property of the object Mdl. You can access this information by using dot notation.
iteration = Mdl.TrainingHistory.Iteration; trainLosses = Mdl.TrainingHistory.TrainingLoss; valLosses = Mdl.TrainingHistory.ValidationLoss; plot(iteration,trainLosses,iteration,valLosses) legend(["Training","Validation"]) xlabel("Iteration") ylabel("Cross-Entropy Loss")
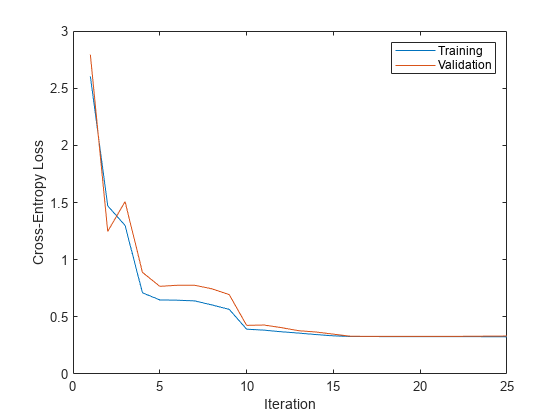
Check the iteration that corresponds to the minimum validation loss. The final returned model Mdl is the model trained at this iteration.
[~,minIdx] = min(valLosses); iteration(minIdx)
ans = 19
Assess the cross-validation loss of neural network models with different regularization strengths, and choose the regularization strength corresponding to the best performing model.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Create a cvpartition object for stratified 5-fold cross-validation. cvp partitions the data into five folds, where each fold has roughly the same proportions of different credit ratings. Set the random seed to the default value for reproducibility of the partition.
rng("default") cvp = cvpartition(creditrating.Rating,"KFold",5);
Compute the cross-validation classification error for neural network classifiers with different regularization strengths. Try regularization strengths on the order of 1/n, where n is the number of observations. Specify to standardize the data before training the neural network models.
1/size(creditrating,1)
ans = 2.5432e-04
lambda = (0:0.5:5)*1e-4; cvloss = zeros(length(lambda),1); for i = 1:length(lambda) cvMdl = fitcnet(creditrating,"Rating","Lambda",lambda(i), ... "CVPartition",cvp,"Standardize",true); cvloss(i) = kfoldLoss(cvMdl,"LossFun","classiferror"); end
Plot the results. Find the regularization strength corresponding to the lowest cross-validation classification error.
plot(lambda,cvloss) xlabel("Regularization Strength") ylabel("Cross-Validation Loss")
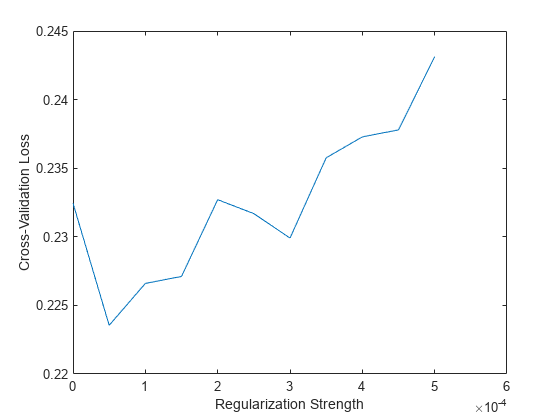
[~,idx] = min(cvloss); bestLambda = lambda(idx)
bestLambda = 5.0000e-05
Train a neural network classifier using the bestLambda regularization strength.
Mdl = fitcnet(creditrating,"Rating","Lambda",bestLambda, ... "Standardize",true)
Mdl =
ClassificationNeuralNetwork
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
CategoricalPredictors: 6
ClassNames: [AAA AA A BBB BB B CCC]
ScoreTransform: 'none'
NumObservations: 3932
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Train a neural network classifier using the OptimizeHyperparameters argument to improve the resulting classifier. Using this argument causes fitcnet to minimize cross-validation loss over some problem hyperparameters using Bayesian optimization.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the partition c = cvpartition(creditrating.Rating,"Holdout",0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set creditTrain = creditrating(trainingIndices,:); creditTest = creditrating(testIndices,:);
Train a neural network classifier by passing the training data creditTrain to the fitcnet function, and include the OptimizeHyperparameters argument. For reproducibility, set the AcquisitionFunctionName to "expected-improvement-plus" in a HyperparameterOptimizationOptions structure. To attempt to get a better solution, set the number of optimization steps to 100 instead of the default 30. fitcnet performs Bayesian optimization by default. To use grid search or random search, set the Optimizer field in HyperparameterOptimizationOptions.
rng("default") % For reproducibility Mdl = fitcnet(creditTrain,"Rating","OptimizeHyperparameters","auto", ... "HyperparameterOptimizationOptions", ... struct("AcquisitionFunctionName","expected-improvement-plus", ... "MaxObjectiveEvaluations",100))
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 1 | Best | 0.55944 | 0.6624 | 0.55944 | 0.55944 | none | true | 0.05834 | 3 |
| 2 | Best | 0.21297 | 10.953 | 0.21297 | 0.22674 | relu | true | 5.0811e-08 | [ 1 25] |
| 3 | Accept | 0.74189 | 0.51791 | 0.21297 | 0.21333 | sigmoid | true | 0.57986 | 126 |
| 4 | Accept | 0.4501 | 0.65455 | 0.21297 | 0.21319 | tanh | false | 0.018683 | 10 |
| 5 | Accept | 0.45359 | 7.4426 | 0.21297 | 0.21318 | relu | true | 0.00037859 | [ 44 1 2] |
| 6 | Accept | 0.30896 | 72.623 | 0.21297 | 0.21303 | relu | true | 4.0364e-09 | [175 183] |
| 7 | Accept | 0.21424 | 7.0269 | 0.21297 | 0.21364 | relu | true | 4.1256e-08 | 1 |
| 8 | Accept | 0.74189 | 0.19974 | 0.21297 | 0.21254 | tanh | false | 0.37071 | [ 10 3 3] |
| 9 | Accept | 0.21774 | 10.829 | 0.21297 | 0.21352 | relu | true | 1.6265e-06 | [ 3 5] |
| 10 | Best | 0.21265 | 9.6793 | 0.21265 | 0.21274 | relu | true | 9.6739e-05 | [ 1 3 6] |
| 11 | Accept | 0.74189 | 0.15813 | 0.21265 | 0.21218 | relu | true | 1.4153 | 27 |
| 12 | Best | 0.20947 | 7.8527 | 0.20947 | 0.20948 | relu | true | 4.7245e-07 | [ 2 3 6] |
| 13 | Accept | 0.23268 | 9.5702 | 0.20947 | 0.20952 | tanh | false | 3.4777e-08 | 10 |
| 14 | Accept | 0.22441 | 13.989 | 0.20947 | 0.20952 | tanh | false | 1.4574e-05 | [ 11 2 9] |
| 15 | Accept | 0.26732 | 69.975 | 0.20947 | 0.20954 | tanh | false | 3.6034e-07 | [291 10] |
| 16 | Accept | 0.23427 | 7.0366 | 0.20947 | 0.20954 | relu | false | 3.2585e-09 | 1 |
| 17 | Accept | 0.21488 | 26.038 | 0.20947 | 0.20954 | relu | false | 8.2337e-06 | [ 1 2 93] |
| 18 | Accept | 0.26224 | 47.701 | 0.20947 | 0.20955 | relu | false | 2.4128e-07 | [274 1] |
| 19 | Accept | 0.74189 | 0.20321 | 0.20947 | 0.20955 | relu | false | 0.060533 | [ 8 3] |
| 20 | Accept | 0.43643 | 7.7327 | 0.20947 | 0.20949 | relu | false | 2.558e-07 | [ 1 17 2] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 21 | Accept | 0.50858 | 4.0815 | 0.20947 | 0.20949 | relu | false | 0.017314 | [ 8 82 93] |
| 22 | Accept | 0.49714 | 8.0331 | 0.20947 | 0.20946 | tanh | false | 0.014033 | [225 17 9] |
| 23 | Accept | 0.28608 | 82.071 | 0.20947 | 0.20947 | relu | false | 1.4036e-07 | [263 14 275] |
| 24 | Accept | 0.26891 | 55.681 | 0.20947 | 0.19753 | relu | false | 2.9418e-05 | [135 11 192] |
| 25 | Accept | 0.25175 | 69.479 | 0.20947 | 0.20948 | relu | true | 3.0659e-06 | [ 5 150 186] |
| 26 | Accept | 0.27018 | 45.668 | 0.20947 | 0.20144 | relu | false | 3.1943e-09 | [261 4] |
| 27 | Accept | 0.22568 | 32.734 | 0.20947 | 0.20943 | relu | true | 1.1294e-06 | [ 9 1 147] |
| 28 | Accept | 0.21392 | 7.9387 | 0.20947 | 0.20941 | tanh | false | 8.9536e-07 | 1 |
| 29 | Accept | 0.21901 | 51.491 | 0.20947 | 0.20937 | tanh | false | 1.2889e-07 | [ 3 2 197] |
| 30 | Accept | 0.21519 | 12.24 | 0.20947 | 0.20934 | relu | false | 0.00035024 | [ 1 36 9] |
| 31 | Accept | 0.2775 | 3.8553 | 0.20947 | 0.20934 | tanh | false | 0.0002159 | [ 1 2] |
| 32 | Accept | 0.21615 | 11.204 | 0.20947 | 0.20932 | relu | false | 4.3753e-05 | [ 1 23 5] |
| 33 | Accept | 0.21647 | 56.854 | 0.20947 | 0.20931 | tanh | false | 3.4689e-09 | [ 1 268 4] |
| 34 | Accept | 0.27463 | 53.603 | 0.20947 | 0.20937 | relu | false | 2.2259e-06 | [286 34] |
| 35 | Accept | 0.3042 | 46.781 | 0.20947 | 0.20933 | relu | true | 1.1227e-07 | 281 |
| 36 | Accept | 0.42912 | 29.189 | 0.20947 | 0.20939 | relu | false | 0.00076968 | [284 2 8] |
| 37 | Accept | 0.21488 | 10.309 | 0.20947 | 0.20939 | tanh | true | 4.0099e-09 | [ 1 3 4] |
| 38 | Accept | 0.21774 | 7.3039 | 0.20947 | 0.20939 | tanh | true | 2.7818e-06 | 1 |
| 39 | Accept | 0.30896 | 99.307 | 0.20947 | 0.20939 | tanh | true | 1.7536e-07 | [292 9 158] |
| 40 | Accept | 0.52066 | 10.635 | 0.20947 | 0.20939 | tanh | true | 0.0096088 | [ 1 161 24] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 41 | Accept | 0.21392 | 7.3746 | 0.20947 | 0.20939 | tanh | true | 3.5001e-08 | 1 |
| 42 | Accept | 0.21742 | 11.47 | 0.20947 | 0.2094 | sigmoid | false | 3.5109e-09 | [ 1 19] |
| 43 | Accept | 0.25652 | 71.051 | 0.20947 | 0.20939 | sigmoid | false | 1.7677e-07 | [297 2] |
| 44 | Accept | 0.2136 | 81.345 | 0.20947 | 0.20939 | sigmoid | false | 1.0104e-05 | [ 1 95 272] |
| 45 | Accept | 0.21488 | 7.9797 | 0.20947 | 0.20939 | sigmoid | false | 4.9812e-07 | 1 |
| 46 | Accept | 0.74189 | 0.19233 | 0.20947 | 0.20938 | sigmoid | false | 0.014036 | 1 |
| 47 | Accept | 0.2206 | 98.161 | 0.20947 | 0.20948 | sigmoid | false | 1.6413e-07 | [ 4 144 271] |
| 48 | Accept | 0.21551 | 56.403 | 0.20947 | 0.20938 | tanh | true | 5.3046e-08 | [ 1 263] |
| 49 | Accept | 0.21869 | 52.317 | 0.20947 | 0.20931 | relu | false | 0.00012348 | [ 1 20 297] |
| 50 | Accept | 0.24793 | 68.619 | 0.20947 | 0.20931 | sigmoid | false | 3.3564e-09 | [288 1 24] |
| 51 | Accept | 0.24412 | 49.246 | 0.20947 | 0.2093 | sigmoid | false | 4.5434e-06 | [ 50 20 166] |
| 52 | Accept | 0.21488 | 4.5457 | 0.20947 | 0.20931 | none | false | 7.8998e-09 | [ 1 5] |
| 53 | Accept | 0.22028 | 31.073 | 0.20947 | 0.20931 | none | false | 1.5483e-07 | [132 41 15] |
| 54 | Accept | 0.22028 | 37.148 | 0.20947 | 0.20931 | none | false | 5.909e-09 | [271 16] |
| 55 | Accept | 0.21615 | 3.7849 | 0.20947 | 0.20931 | none | false | 5.9842e-06 | 1 |
| 56 | Accept | 0.21456 | 4.6696 | 0.20947 | 0.20931 | none | false | 2.9016e-07 | 1 |
| 57 | Accept | 0.21615 | 39.25 | 0.20947 | 0.20932 | none | false | 0.0002184 | [246 194] |
| 58 | Accept | 0.2206 | 23.229 | 0.20947 | 0.20931 | none | false | 1.1092e-05 | 277 |
| 59 | Accept | 0.3007 | 0.58966 | 0.20947 | 0.2093 | none | false | 0.0048807 | [ 1 3] |
| 60 | Accept | 0.22155 | 1.3952 | 0.20947 | 0.20947 | none | false | 9.8985e-05 | 1 |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 61 | Accept | 0.21996 | 20.233 | 0.20947 | 0.20931 | none | true | 3.1814e-09 | [297 16] |
| 62 | Accept | 0.21488 | 1.8467 | 0.20947 | 0.20947 | none | true | 6.7267e-08 | [ 1 7 13] |
| 63 | Accept | 0.22028 | 63.616 | 0.20947 | 0.20932 | none | true | 3.7479e-07 | [227 157] |
| 64 | Accept | 0.21964 | 81.089 | 0.20947 | 0.20947 | none | true | 3.3729e-08 | [236 263 240] |
| 65 | Accept | 0.226 | 58.8 | 0.20947 | 0.20947 | sigmoid | true | 3.2435e-09 | [ 3 268 16] |
| 66 | Accept | 0.28512 | 62.087 | 0.20947 | 0.20947 | sigmoid | true | 1.6061e-07 | [293 1] |
| 67 | Accept | 0.74189 | 0.39413 | 0.20947 | 0.20947 | none | false | 31.159 | [292 12] |
| 68 | Accept | 0.30833 | 56.986 | 0.20947 | 0.20947 | sigmoid | true | 3.2135e-09 | 285 |
| 69 | Accept | 0.2206 | 4.3217 | 0.20947 | 0.20927 | relu | true | 1.3908e-05 | 1 |
| 70 | Accept | 0.21519 | 47.818 | 0.20947 | 0.20935 | sigmoid | true | 3.634e-08 | [ 1 221 16] |
| 71 | Accept | 0.21488 | 4.2978 | 0.20947 | 0.20935 | none | true | 4.2772e-09 | [ 1 15 116] |
| 72 | Accept | 0.22123 | 35.165 | 0.20947 | 0.20929 | none | false | 1.772e-05 | [ 6 270] |
| 73 | Accept | 0.21488 | 17.014 | 0.20947 | 0.20926 | none | true | 5.6831e-06 | [ 1 123] |
| 74 | Accept | 0.21964 | 16.494 | 0.20947 | 0.20929 | none | true | 1.584e-05 | 278 |
| 75 | Accept | 0.21424 | 10.535 | 0.20947 | 0.20929 | sigmoid | true | 4.1488e-06 | [ 1 18] |
| 76 | Accept | 0.21583 | 15.623 | 0.20947 | 0.2068 | sigmoid | true | 5.3271e-07 | [ 1 4 45] |
| 77 | Accept | 0.23045 | 53.687 | 0.20947 | 0.20933 | sigmoid | true | 2.799e-05 | 295 |
| 78 | Accept | 0.21424 | 49.711 | 0.20947 | 0.20927 | sigmoid | false | 1.5769e-06 | [ 1 290] |
| 79 | Accept | 0.24317 | 23.256 | 0.20947 | 0.20695 | sigmoid | true | 9.9752e-05 | [ 1 2 75] |
| 80 | Accept | 0.74189 | 0.59847 | 0.20947 | 0.20646 | tanh | true | 31.477 | [276 1] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 81 | Accept | 0.21265 | 8.0742 | 0.20947 | 0.20633 | sigmoid | false | 2.3742e-08 | 1 |
| 82 | Accept | 0.21964 | 10.426 | 0.20947 | 0.20625 | none | true | 2.4884e-06 | [ 28 19] |
| 83 | Accept | 0.22028 | 1.3151 | 0.20947 | 0.2062 | none | true | 7.322e-05 | 1 |
| 84 | Accept | 0.24857 | 61.832 | 0.20947 | 0.20615 | tanh | false | 3.2805e-09 | [246 6] |
| 85 | Accept | 0.26828 | 57.879 | 0.20947 | 0.20612 | tanh | true | 3.3231e-05 | 268 |
| 86 | Accept | 0.2651 | 39.828 | 0.20947 | 0.206 | tanh | true | 2.978e-05 | [ 1 211 1] |
| 87 | Accept | 0.22092 | 9.3782 | 0.20947 | 0.20593 | none | false | 3.4358e-08 | [ 6 10 8] |
| 88 | Accept | 0.21551 | 9.2736 | 0.20947 | 0.20895 | relu | true | 6.6466e-07 | [ 1 8] |
| 89 | Accept | 0.32295 | 8.2648 | 0.20947 | 0.20834 | relu | true | 3.6643e-09 | [ 1 29 4] |
| 90 | Accept | 0.21615 | 10.897 | 0.20947 | 0.20844 | tanh | false | 5.9606e-06 | [ 1 9] |
| 91 | Accept | 0.21933 | 11.781 | 0.20947 | 0.2083 | none | false | 1.1645e-06 | [ 22 50] |
| 92 | Accept | 0.21805 | 25.108 | 0.20947 | 0.20814 | none | true | 0.00017742 | [300 49] |
| 93 | Accept | 0.21901 | 12.868 | 0.20947 | 0.20803 | none | true | 3.8704e-05 | [ 23 9 45] |
| 94 | Accept | 0.21488 | 8.2557 | 0.20947 | 0.20803 | none | true | 5.7435e-07 | [ 1 3 25] |
| 95 | Accept | 0.32517 | 50.563 | 0.20947 | 0.20776 | tanh | true | 3.1834e-09 | 274 |
| 96 | Accept | 0.21488 | 10.904 | 0.20947 | 0.20801 | tanh | true | 4.5154e-07 | [ 1 16] |
| 97 | Accept | 0.21392 | 11.16 | 0.20947 | 0.20803 | none | false | 3.1889e-09 | [ 15 32 1] |
| 98 | Accept | 0.21583 | 20.833 | 0.20947 | 0.20983 | relu | true | 1.8928e-07 | [ 1 61] |
| 99 | Accept | 0.21329 | 7.1721 | 0.20947 | 0.21001 | sigmoid | true | 5.836e-09 | 1 |
| 100 | Accept | 0.21996 | 3.3651 | 0.20947 | 0.21027 | none | true | 1.0486e-08 | 11 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 100 reached.
Total function evaluations: 100
Total elapsed time: 2719.497 seconds
Total objective function evaluation time: 2661.8987
Best observed feasible point:
Activations Standardize Lambda LayerSizes
___________ ___________ __________ ___________
relu true 4.7245e-07 2 3 6
Observed objective function value = 0.20947
Estimated objective function value = 0.21027
Function evaluation time = 7.8527
Best estimated feasible point (according to models):
Activations Standardize Lambda LayerSizes
___________ ___________ __________ ___________
relu true 4.7245e-07 2 3 6
Estimated objective function value = 0.21027
Estimated function evaluation time = 11.1905
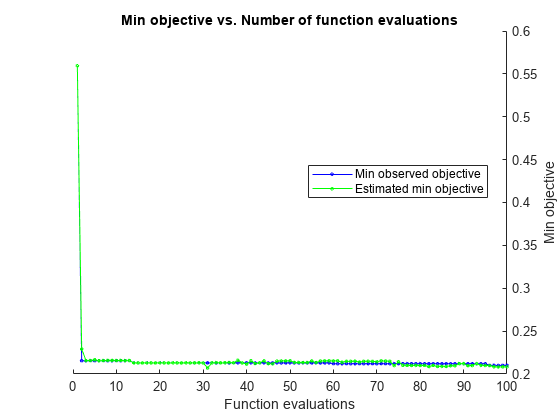
Mdl =
ClassificationNeuralNetwork
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
CategoricalPredictors: 6
ClassNames: [AAA AA A BBB BB B CCC]
ScoreTransform: 'none'
NumObservations: 3146
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
LayerSizes: [2 3 6]
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Mdl is a trained ClassificationNeuralNetwork classifier. The model corresponds to the best estimated feasible point, as opposed to the best observed feasible point. (For details on this distinction, see bestPoint.) You can use dot notation to access the properties of Mdl. For example, you can specify Mdl.HyperparameterOptimizationResults to get more information about the optimization of the neural network model.
Find the classification accuracy of the model on the test data set. Visualize the results by using a confusion matrix.
modelAccuracy = 1 - loss(Mdl,creditTest,"Rating", ... "LossFun","classiferror")
modelAccuracy = 0.8040
confusionchart(creditTest.Rating,predict(Mdl,creditTest))
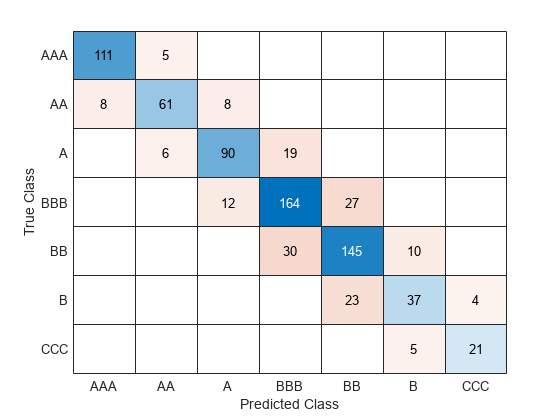
The model has all predicted classes within one unit of the true classes, meaning all predictions are off by no more than one rating.
Train a neural network classifier using the OptimizeHyperparameters argument to improve the resulting classification accuracy. Use the hyperparameters function to specify larger-than-default values for the number of layers used and the layer size range.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency.
creditrating = readtable("CreditRating_Historical.dat");Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the partition c = cvpartition(creditrating.Rating,"Holdout",0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set creditTrain = creditrating(trainingIndices,:); creditTest = creditrating(testIndices,:);
List the hyperparameters available for this problem of fitting the Rating response.
params = hyperparameters("fitcnet",creditTrain,"Rating"); for ii = 1:length(params) disp(ii);disp(params(ii)) end
1
optimizableVariable with properties:
Name: 'NumLayers'
Range: [1 3]
Type: 'integer'
Transform: 'none'
Optimize: 1
2
optimizableVariable with properties:
Name: 'Activations'
Range: {'relu' 'tanh' 'sigmoid' 'none'}
Type: 'categorical'
Transform: 'none'
Optimize: 1
3
optimizableVariable with properties:
Name: 'Standardize'
Range: {'true' 'false'}
Type: 'categorical'
Transform: 'none'
Optimize: 1
4
optimizableVariable with properties:
Name: 'Lambda'
Range: [3.1786e-09 31.7864]
Type: 'real'
Transform: 'log'
Optimize: 1
5
optimizableVariable with properties:
Name: 'LayerWeightsInitializer'
Range: {'glorot' 'he'}
Type: 'categorical'
Transform: 'none'
Optimize: 0
6
optimizableVariable with properties:
Name: 'LayerBiasesInitializer'
Range: {'zeros' 'ones'}
Type: 'categorical'
Transform: 'none'
Optimize: 0
7
optimizableVariable with properties:
Name: 'Layer_1_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
8
optimizableVariable with properties:
Name: 'Layer_2_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
9
optimizableVariable with properties:
Name: 'Layer_3_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 1
10
optimizableVariable with properties:
Name: 'Layer_4_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 0
11
optimizableVariable with properties:
Name: 'Layer_5_Size'
Range: [1 300]
Type: 'integer'
Transform: 'log'
Optimize: 0
To try more layers than the default of 1 through 3, set the range of NumLayers (optimizable variable 1) to its maximum allowable size, [1 5]. Also, set Layer_4_Size and Layer_5_Size (optimizable variables 10 and 11, respectively) to be optimized.
params(1).Range = [1 5]; params(10).Optimize = true; params(11).Optimize = true;
Set the range of all layer sizes (optimizable variables 7 through 11) to [1 400] instead of the default [1 300].
for ii = 7:11 params(ii).Range = [1 400]; end
Train a neural network classifier by passing the training data creditTrain to the fitcnet function, and include the OptimizeHyperparameters argument set to params. For reproducibility, set the AcquisitionFunctionName to "expected-improvement-plus" in a HyperparameterOptimizationOptions structure. To attempt to get a better solution, set the number of optimization steps to 100 instead of the default 30.
rng("default") % For reproducibility Mdl = fitcnet(creditTrain,"Rating","OptimizeHyperparameters",params, ... "HyperparameterOptimizationOptions", ... struct("AcquisitionFunctionName","expected-improvement-plus", ... "MaxObjectiveEvaluations",100))
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 1 | Best | 0.74189 | 0.32605 | 0.74189 | 0.74189 | sigmoid | true | 0.68961 | [104 1 5 3 1] |
| 2 | Best | 0.2225 | 79.214 | 0.2225 | 0.24316 | relu | true | 0.00058564 | [ 38 208 162] |
| 3 | Accept | 0.63891 | 15.162 | 0.2225 | 0.22698 | sigmoid | true | 1.9768e-06 | [ 1 25 1 287 7] |
| 4 | Best | 0.21996 | 39.338 | 0.21996 | 0.22345 | none | false | 1.3353e-06 | 320 |
| 5 | Accept | 0.74189 | 0.13266 | 0.21996 | 0.21999 | relu | true | 2.7056 | [ 1 2 1] |
| 6 | Accept | 0.29466 | 110.23 | 0.21996 | 0.22 | relu | true | 1.0503e-06 | [301 31 400] |
| 7 | Accept | 0.68722 | 5.3887 | 0.21996 | 0.21999 | relu | true | 0.0113 | [ 97 5 56] |
| 8 | Accept | 0.29116 | 78.242 | 0.21996 | 0.21998 | relu | true | 7.5665e-05 | [311 93 3] |
| 9 | Accept | 0.3007 | 90.496 | 0.21996 | 0.21999 | relu | true | 5.6564e-08 | [ 29 375 84] |
| 10 | Best | 0.21138 | 84.357 | 0.21138 | 0.21129 | relu | true | 0.0002307 | [ 1 102 350] |
| 11 | Accept | 0.74189 | 0.14744 | 0.21138 | 0.2115 | none | false | 30.105 | 3 |
| 12 | Accept | 0.21392 | 7.445 | 0.21138 | 0.21149 | none | false | 3.2104e-09 | 3 |
| 13 | Accept | 0.21233 | 37.435 | 0.21138 | 0.21151 | none | false | 4.7078e-08 | [292 2] |
| 14 | Accept | 0.21488 | 12.59 | 0.21138 | 0.21156 | none | false | 6.6064e-08 | [ 7 1 227] |
| 15 | Accept | 0.30642 | 138.77 | 0.21138 | 0.21148 | relu | true | 1.5819e-05 | [137 164 319 49] |
| 16 | Accept | 0.74189 | 0.43973 | 0.21138 | 0.21149 | relu | true | 0.54894 | [ 1 392 16] |
| 17 | Accept | 0.22123 | 112.55 | 0.21138 | 0.21153 | relu | true | 2.2254e-05 | [ 2 385 175] |
| 18 | Accept | 0.22028 | 111.52 | 0.21138 | 0.21149 | none | false | 1.5532e-07 | [ 69 72 218 288] |
| 19 | Accept | 0.21933 | 74.082 | 0.21138 | 0.21147 | none | false | 3.8718e-09 | [ 23 172 251] |
| 20 | Accept | 0.21964 | 198.9 | 0.21138 | 0.21121 | none | false | 2.9122e-06 | [ 61 351 305] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 21 | Accept | 0.21837 | 49.152 | 0.21138 | 0.21121 | none | false | 8.3868e-05 | [379 2 21 17] |
| 22 | Accept | 0.21774 | 11.13 | 0.21138 | 0.21514 | none | false | 3.7014e-05 | [ 1 103] |
| 23 | Accept | 0.21583 | 30.655 | 0.21138 | 0.21511 | none | false | 0.0013675 | [245 11 82 111 25] |
| 24 | Accept | 0.22187 | 47.861 | 0.21138 | 0.2151 | none | false | 0.00035852 | [143 7 2 6 399] |
| 25 | Accept | 0.2206 | 7.3635 | 0.21138 | 0.21151 | none | false | 1.3924e-08 | 4 |
| 26 | Accept | 0.22028 | 72.206 | 0.21138 | 0.21133 | none | false | 0.00029756 | [ 36 322 65 57 5] |
| 27 | Accept | 0.22028 | 24.303 | 0.21138 | 0.21149 | none | true | 3.5432e-09 | [186 7 99] |
| 28 | Accept | 0.28258 | 287.57 | 0.21138 | 0.21641 | relu | true | 0.00015562 | [127 381 376] |
| 29 | Accept | 0.21964 | 29.214 | 0.21138 | 0.21644 | none | true | 1.1567e-07 | [ 24 130 100] |
| 30 | Accept | 0.21615 | 38.832 | 0.21138 | 0.21645 | none | true | 1.3591e-05 | [ 27 2 300] |
| 31 | Accept | 0.25429 | 8.9728 | 0.21138 | 0.21011 | none | true | 0.0011686 | [ 38 21 182 15 1] |
| 32 | Accept | 0.74189 | 0.31341 | 0.21138 | 0.21137 | none | true | 0.21395 | [ 2 90 1 9 98] |
| 33 | Accept | 0.21392 | 9.1485 | 0.21138 | 0.20991 | none | true | 0.00013584 | [ 1 8 2 42] |
| 34 | Accept | 0.21488 | 2.4616 | 0.21138 | 0.20915 | none | true | 1.429e-08 | [ 1 9 2 3] |
| 35 | Accept | 0.21488 | 24.297 | 0.21138 | 0.20837 | none | true | 1.343e-06 | [ 1 267] |
| 36 | Accept | 0.32168 | 26.448 | 0.21138 | 0.20862 | relu | false | 3.5696e-07 | [ 1 2 51 9 75] |
| 37 | Accept | 0.29943 | 2.9924 | 0.21138 | 0.20852 | relu | false | 0.00015229 | 1 |
| 38 | Accept | 0.74189 | 0.94839 | 0.21138 | 0.20881 | relu | false | 0.063654 | [236 110 6] |
| 39 | Accept | 0.28671 | 52.298 | 0.21138 | 0.20818 | relu | false | 8.8086e-06 | [319 13] |
| 40 | Accept | 0.2438 | 29.767 | 0.21138 | 0.20839 | sigmoid | false | 4.5197e-09 | [ 70 10 7] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 41 | Accept | 0.24189 | 64.101 | 0.21138 | 0.20807 | sigmoid | false | 2.9475e-07 | [ 57 19 163 6] |
| 42 | Accept | 0.22282 | 40.946 | 0.21138 | 0.2078 | sigmoid | false | 5.2093e-05 | [ 1 233] |
| 43 | Accept | 0.74189 | 1.8331 | 0.21138 | 0.20938 | sigmoid | false | 0.0038636 | [337 39 1] |
| 44 | Accept | 0.22155 | 17.147 | 0.21138 | 0.2091 | sigmoid | false | 7.0303e-06 | [ 1 11 34 2] |
| 45 | Accept | 0.21901 | 10.607 | 0.21138 | 0.20932 | tanh | false | 7.6416e-08 | [ 3 4] |
| 46 | Accept | 0.21933 | 33.754 | 0.21138 | 0.20899 | tanh | false | 2.9788e-06 | [ 2 2 67 22] |
| 47 | Accept | 0.22123 | 91.481 | 0.21138 | 0.20872 | tanh | false | 0.00030544 | [368 54] |
| 48 | Accept | 0.74189 | 0.45871 | 0.21138 | 0.20997 | tanh | false | 0.024399 | [ 1 60 26] |
| 49 | Accept | 0.24348 | 153.78 | 0.21138 | 0.21154 | tanh | false | 4.2e-05 | [336 169 2 9 2] |
| 50 | Accept | 0.27781 | 151.87 | 0.21138 | 0.21008 | tanh | false | 4.7612e-07 | [346 204 20] |
| 51 | Accept | 0.21488 | 55.554 | 0.21138 | 0.20963 | tanh | false | 3.4829e-09 | [ 1 232] |
| 52 | Accept | 0.21488 | 156.21 | 0.21138 | 0.20988 | tanh | true | 2.4638e-08 | [ 1 7 68 139 362] |
| 53 | Accept | 0.25842 | 54.398 | 0.21138 | 0.20963 | tanh | true | 8.926e-07 | [ 11 5 209] |
| 54 | Accept | 0.26891 | 66.331 | 0.21138 | 0.2093 | tanh | true | 3.4368e-09 | [247 4 5 17] |
| 55 | Accept | 0.21488 | 151.58 | 0.21138 | 0.20932 | tanh | true | 0.0005921 | [ 1 76 177 312] |
| 56 | Accept | 0.51335 | 11.191 | 0.21138 | 0.20974 | tanh | true | 0.025861 | [398 25] |
| 57 | Accept | 0.2117 | 11.729 | 0.21138 | 0.2091 | tanh | true | 5.6188e-05 | [ 2 1 11] |
| 58 | Accept | 0.28481 | 63.324 | 0.21138 | 0.20906 | relu | false | 3.2827e-09 | [383 13 40] |
| 59 | Accept | 0.2438 | 125.61 | 0.21138 | 0.20878 | tanh | true | 0.0001805 | [346 14 292 2] |
| 60 | Accept | 0.21583 | 8.8331 | 0.21138 | 0.2083 | tanh | false | 1.4495e-08 | 1 |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 61 | Accept | 0.21456 | 40.705 | 0.21138 | 0.20843 | tanh | false | 0.00012835 | [ 1 135] |
| 62 | Accept | 0.29085 | 105.56 | 0.21138 | 0.20768 | sigmoid | false | 1.7946e-05 | [330 94 1] |
| 63 | Accept | 0.21424 | 78.388 | 0.21138 | 0.20729 | sigmoid | false | 4.1216e-08 | [ 1 81 8 284] |
| 64 | Accept | 0.21456 | 103.52 | 0.21138 | 0.20732 | none | true | 0.00016065 | [389 7 221 2 396] |
| 65 | Accept | 0.36332 | 0.83293 | 0.21138 | 0.21536 | none | false | 0.0099272 | [ 1 9 29] |
| 66 | Accept | 0.21678 | 64.484 | 0.21138 | 0.2131 | none | true | 4.2307e-05 | [154 221 4] |
| 67 | Accept | 0.25556 | 97.467 | 0.21138 | 0.20741 | tanh | true | 7.0323e-08 | [ 3 30 384 1] |
| 68 | Accept | 0.22028 | 45.907 | 0.21138 | 0.20745 | none | true | 1.3544e-06 | [363 18] |
| 69 | Accept | 0.21996 | 21.112 | 0.21138 | 0.20744 | none | true | 2.0831e-08 | [350 30] |
| 70 | Accept | 0.21615 | 57.611 | 0.21138 | 0.20721 | tanh | true | 8.562e-06 | [ 1 11 200 4 29] |
| 71 | Accept | 0.29784 | 65.684 | 0.21138 | 0.20755 | sigmoid | true | 3.1815e-09 | 342 |
| 72 | Accept | 0.74189 | 0.14283 | 0.21138 | 0.20695 | tanh | true | 31.449 | 2 |
| 73 | Accept | 0.2225 | 11.234 | 0.21138 | 0.21304 | relu | true | 3.2834e-09 | [ 3 2] |
| 74 | Accept | 0.31278 | 20.754 | 0.21138 | 0.20495 | tanh | false | 1.099e-08 | [ 30 41] |
| 75 | Accept | 0.21392 | 20.019 | 0.21138 | 0.20461 | tanh | false | 3.5172e-07 | [ 1 18 8 29] |
| 76 | Accept | 0.21488 | 44.322 | 0.21138 | 0.21285 | tanh | true | 0.0001681 | [ 1 64 1 83 21] |
| 77 | Accept | 0.30356 | 31.829 | 0.21138 | 0.20648 | tanh | true | 3.2255e-05 | [ 32 25 41 25] |
| 78 | Accept | 0.21488 | 12.306 | 0.21138 | 0.20648 | none | false | 8.7968e-07 | [ 1 15 45 8] |
| 79 | Accept | 0.21265 | 14.523 | 0.21138 | 0.20629 | tanh | true | 3.1927e-09 | [ 1 20 14] |
| 80 | Accept | 0.2136 | 17.849 | 0.21138 | 0.2077 | relu | true | 0.00022487 | [ 1 6 3 38 45] |
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 81 | Accept | 0.25175 | 86.445 | 0.21138 | 0.20757 | sigmoid | false | 2.8027e-08 | [372 14 2] |
| 82 | Accept | 0.21488 | 3.9545 | 0.21138 | 0.21286 | none | true | 3.2854e-09 | [ 1 4 98] |
| 83 | Accept | 0.21933 | 6.6782 | 0.21138 | 0.214 | none | true | 7.8092e-05 | [ 32 11] |
| 84 | Accept | 0.21901 | 255.5 | 0.21138 | 0.21402 | none | false | 1.1069e-05 | [246 278 381 6 7] |
| 85 | Accept | 0.21869 | 46.923 | 0.21138 | 0.20835 | none | true | 2.5019e-07 | [380 7 5] |
| 86 | Accept | 0.21424 | 7.6385 | 0.21138 | 0.20716 | relu | true | 2.3756e-06 | 1 |
| 87 | Accept | 0.22155 | 11.623 | 0.21138 | 0.20866 | tanh | true | 0.00031371 | [ 1 13] |
| 88 | Accept | 0.74189 | 0.8902 | 0.21138 | 0.20838 | sigmoid | false | 30.269 | [ 1 214 10 198] |
| 89 | Accept | 0.28353 | 80.644 | 0.21138 | 0.20816 | sigmoid | false | 2.7729e-07 | [ 1 239 1 7 88] |
| 90 | Accept | 0.21424 | 75.378 | 0.21138 | 0.20825 | sigmoid | false | 6.4753e-09 | [ 1 5 40 311] |
| 91 | Accept | 0.21615 | 52.965 | 0.21138 | 0.20845 | tanh | false | 1.1159e-07 | [ 1 13 175] |
| 92 | Accept | 0.21519 | 14.358 | 0.21138 | 0.20859 | none | false | 5.6623e-06 | [ 1 31 27 24] |
| 93 | Accept | 0.21297 | 17.457 | 0.21138 | 0.21432 | tanh | true | 7.9886e-09 | [ 1 7 35] |
| 94 | Accept | 0.21615 | 43.228 | 0.21138 | 0.20911 | none | true | 6.0944e-06 | [ 3 61 11 90 83] |
| 95 | Accept | 0.25683 | 11.12 | 0.21138 | 0.20918 | tanh | false | 2.8053e-05 | [ 1 10 1] |
| 96 | Accept | 0.32676 | 53.385 | 0.21138 | 0.21405 | relu | true | 3.4352e-09 | [315 2 8] |
| 97 | Accept | 0.21933 | 9.813 | 0.21138 | 0.20966 | none | false | 1.5781e-08 | 41 |
| 98 | Accept | 0.34488 | 72.967 | 0.21138 | 0.20338 | relu | true | 3.2814e-09 | [ 1 21 2 75 348] |
| 99 | Accept | 0.21583 | 227.25 | 0.21138 | 0.20342 | none | true | 1.3976e-08 | [ 2 260 237 130 346] |
| 100 | Accept | 0.2136 | 94.144 | 0.21138 | 0.20316 | tanh | false | 3.7209e-07 | [ 1 42 1 2 359] |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 100 reached.
Total function evaluations: 100
Total elapsed time: 5308.1522 seconds
Total objective function evaluation time: 5250.0671
Best observed feasible point:
Activations Standardize Lambda LayerSizes
___________ ___________ _________ _______________
relu true 0.0002307 1 102 350
Observed objective function value = 0.21138
Estimated objective function value = 0.20316
Function evaluation time = 84.3573
Best estimated feasible point (according to models):
Activations Standardize Lambda LayerSizes
___________ ___________ _________ _______________
relu true 0.0002307 1 102 350
Estimated objective function value = 0.20316
Estimated function evaluation time = 73.1472
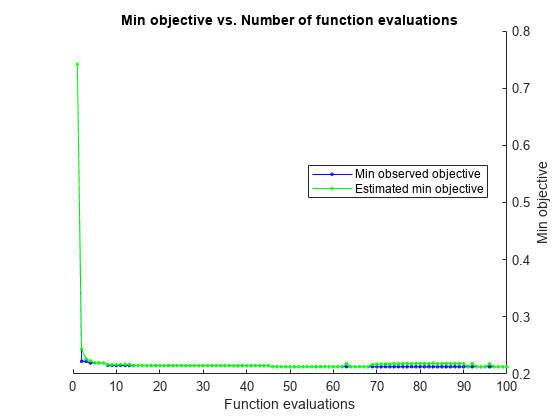
Mdl =
ClassificationNeuralNetwork
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
CategoricalPredictors: 6
ClassNames: [AAA AA A BBB BB B CCC]
ScoreTransform: 'none'
NumObservations: 3146
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
LayerSizes: [1 102 350]
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Find the classification accuracy of the model on the test data set. Visualize the results by using a confusion matrix.
testAccuracy = 1 - loss(Mdl,creditTest,"Rating", ... "LossFun","classiferror")
testAccuracy = 0.8015
confusionchart(creditTest.Rating,predict(Mdl,creditTest))
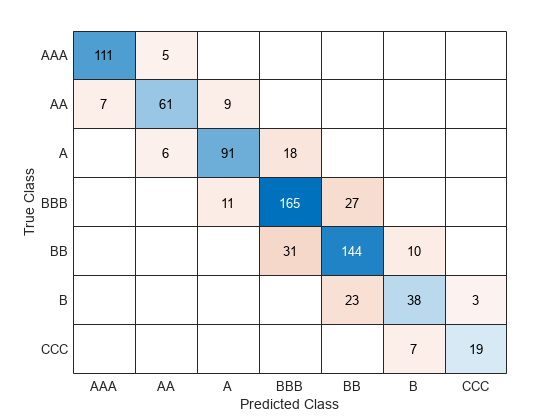
The model has all predicted classes within one unit of the true classes, meaning all predictions are off by no more than one rating.
Input Arguments
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
Response variable name, specified as the name of a variable in
Tbl.
You must specify ResponseVarName as a character vector or string scalar.
For example, if the response variable Y is
stored as Tbl.Y, then specify it as
"Y". Otherwise, the software
treats all columns of Tbl, including
Y, as predictors when training
the model.
The response variable must be a categorical, character, or string array; a logical or numeric
vector; or a cell array of character vectors. If
Y is a character array, then each
element of the response variable must correspond to one row of
the array.
A good practice is to specify the order of the classes by using the
ClassNames name-value
argument.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Class labels used to train the model, specified as a numeric, categorical, or logical vector; a character or string array; or a cell array of character vectors.
If
Yis a character array, then each element of the class labels must correspond to one row of the array.The length of
Ymust be equal to the number of rows inTblorX.A good practice is to specify the class order by using the
ClassNamesname-value argument.
Data Types: single | double | categorical | logical | char | string | cell
Predictor data used to train the model, specified as a numeric matrix.
By default, the software treats each row of X as one
observation, and each column as one predictor.
The length of Y and the number of observations in
X must be equal.
To specify the names of the predictors in the order of their appearance in
X, use the PredictorNames name-value
argument.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time.
Data Types: single | double
Note
The software treats NaN, empty character vector
(''), empty string (""),
<missing>, and <undefined> elements as
missing values, and removes observations with any of these characteristics:
Missing value in the response variable (for example,
YorValidationData{2})At least one missing value in a predictor observation (for example, row in
XorValidationData{1})NaNvalue or0weight (for example, value inWeightsorValidationData{3})Class label with
0prior probability (value inPrior)
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: fitcnet(X,Y,LayerSizes=[10 10],Activations=["relu","tanh"])
specifies to create a neural network with two fully connected layers, each with 10 outputs.
The first layer uses a rectified linear unit (ReLU) activation function, and the second uses
a hyperbolic tangent activation function.
Neural Network Options
Sizes of the fully connected layers in the neural network model, specified as one of these values:
Vector of positive integers — The ith element of
LayerSizesis the number of outputs in the ith fully connected layer of the neural network model.LayerSizesdoes not include the size of the final fully connected layer. For more information, see Neural Network Structure.[](since R2025a) — Use the neural network architecture specified by theNetworkargument.
When Network is [], the default value is
10. Otherwise, the default value is []. If you
specify the neural network architecture using the Network
argument, then LayerSizes must be [].
Example: LayerSizes=[100 25 10]
Activation functions for the fully connected layers of the neural network model, specified as one of these values:
String scalar or character vector — Use the specified activation function for each of the fully connected layers of the model, excluding the final fully connected layer. The activation function for the final fully connected layer is always softmax. For more information, see Neural Network Structure.
String array or cell array of character vectors — Use the ith element of
Activationsfor the ith fully connected layer of the model.""(since R2025a) — Use the neural network architecture specified by theNetworkargument.
Specify the activation functions using one or more of these values:
| Value | Description |
|---|---|
"relu" | Rectified linear unit (ReLU) function — Performs a threshold operation on each element of the input, where any value less than zero is set to zero, that is, |
"tanh" | Hyperbolic tangent (tanh) function — Applies the |
"sigmoid" | Sigmoid function — Performs the following operation on each input element: |
"none" | Identity function — Returns each input element without performing any transformation, that is, f(x) = x |
When Network is [], the default value is
"relu". Otherwise, the default value is []. If
you specify the neural network architecture using the Network
argument, then Activations must be "".
Example: Activations="sigmoid"
Example: Activations=["relu","tanh"]
Function to initialize the fully connected layer weights, specified as one of these values:
"glorot"— Initialize the weights with the Glorot initializer [1] (also known as the Xavier initializer). For each layer, the Glorot initializer independently samples from a uniform distribution with zero mean and variance2/(I+O), whereIis the input size andOis the output size for the layer."he"— Initialize the weights with the He initializer [2]. For each layer, the He initializer samples from a normal distribution with zero mean and variance2/I, whereIis the input size for the layer.""(since R2025a) — Initialize the weights using the initializers specified by the layers in theNetworkargument.
When Network is [], the default value is
"glorot". Otherwise, the default value is "".
If you specify the neural network architecture using the Network
argument, then you must not change the value of the
LayerWeightsInitializer argument.
Example:
LayerWeightsInitializer="he"
Data Types: char | string
Type of initial fully connected layer biases, specified as one of these values:
"zeros"— Initialize the biases with a vector of zeros."ones"— Initialize the biases with a vector of ones.""(since R2025a) — Initialize the biases using the initializers specified by the layers in theNetworkargument.
When Network is [], the default value is
"zeros". Otherwise, the default value is "".
If you specify the neural network architecture using the Network
argument, then you must not change the value of the
LayerBiasesInitializer argument.
Example:
LayerBiasesInitializer="ones"
Data Types: char | string
Since R2025a
Custom neural network architecture, specified as one of these values:
[]— Use the neural network architecture and layer configuration defined by theLayerSizes,Activations,LayerWeightsInitializer, andLayerBiasesInitializerarguments.Layer array (requires Deep Learning Toolbox™) — Use the neural network architecture specified by the layer array. For a list of available layers, see List of Deep Learning Layers (Deep Learning Toolbox).
dlnetworkobject (requires Deep Learning Toolbox) — Use the neural network architecture specified by thedlnetwork(Deep Learning Toolbox) object.
For layer array and dlnetwork input, the network must have a single
feature input layer as input with an input size that matches the number of predictors of
the input data. The output size of the network must match the number of responses. Do
not change the LayerSizes, Activations,
LayerWeightsInitializer, and
LayerBiasesInitializer arguments.
This argument does not support input data with categorical predictors.
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a
table.
Example: ObservationsIn="columns"
Data Types: char | string
Regularization term strength, specified as a nonnegative scalar. The software composes the objective function for minimization from the cross-entropy loss function and the ridge (L2) penalty term.
Example: Lambda=1e-4
Data Types: single | double
Flag to standardize the predictor data, specified as a numeric or logical
0 (false) or 1
(true). If you set Standardize to
true, then the software centers and scales each numeric predictor
variable by the corresponding column mean and standard deviation. The software does
not standardize the categorical predictors.
Example: Standardize=true
Data Types: single | double | logical
Convergence Control Options
Verbosity level, specified as 0 or 1. The
Verbose name-value argument controls the amount of diagnostic
information that fitcnet displays at the command
line.
| Value | Description |
|---|---|
0 | fitcnet does not display diagnostic
information. |
1 | fitcnet periodically displays diagnostic
information. |
By default, StoreHistory is set to
true and fitcnet stores the diagnostic
information inside of Mdl. Use
Mdl.TrainingHistory to access the diagnostic information.
Example: Verbose=1
Data Types: single | double
Frequency of verbose printing, which is the number of iterations between printing to the command window, specified as a positive integer scalar. A value of 1 indicates to print diagnostic information at every iteration.
Note
To use this name-value argument, set Verbose to
1.
Example: VerboseFrequency=5
Data Types: single | double
Flag to store the training history, specified as a numeric or logical
0 (false) or 1
(true). If StoreHistory is set to
true, then the software stores diagnostic information inside of
Mdl, which you can access by using
Mdl.TrainingHistory.
Example: StoreHistory=false
Data Types: single | double | logical
Initial step size, specified as a positive scalar or "auto". By
default, fitcnet does not use the initial step size to determine
the initial Hessian approximation used in training the model (see Training Solver). However, if you
specify an initial step size , then the initial inverse-Hessian approximation is . is the initial gradient vector, and is the identity matrix.
To have fitcnet determine an initial step size automatically,
specify the value as "auto". In this case, the function determines
the initial step size by using . is the initial step vector, and is the vector of unconstrained initial weights and biases.
Example: InitialStepSize="auto"
Data Types: single | double | char | string
Maximum number of training iterations, specified as a positive integer scalar.
The software returns a trained model regardless of whether the training routine
successfully converges. Mdl.ConvergenceInfo contains convergence
information.
Example: IterationLimit=1e8
Data Types: single | double
Relative gradient tolerance, specified as a nonnegative scalar.
Let be the loss function at training iteration t, be the gradient of the loss function with respect to the weights and biases at iteration t, and be the gradient of the loss function at an initial point. If , where , then the training process terminates.
Example: GradientTolerance=1e-5
Data Types: single | double
Loss tolerance, specified as a nonnegative scalar.
If the function loss at some iteration is smaller than
LossTolerance, then the training process terminates.
Example: LossTolerance=1e-8
Data Types: single | double
Step size tolerance, specified as a nonnegative scalar.
If the step size at some iteration is smaller than
StepTolerance, then the training process terminates.
Example: StepTolerance=1e-4
Data Types: single | double
Validation data for training convergence detection, specified as a cell array or table.
During the training process, the software periodically estimates the validation
loss by using ValidationData. If the validation loss increases
more than ValidationPatience times in a row, then the software
terminates the training.
You can specify ValidationData as a table if you use a table
Tbl of predictor data that contains the response variable. In
this case, ValidationData must contain the same predictors and
response contained in Tbl. The software does not apply weights to
observations, even if Tbl contains a vector of weights. To
specify weights, you must specify ValidationData as a cell
array.
If you specify ValidationData as a cell array, then it must
have the following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of class labels, then it must have the same number of elements as the number of observations inValidationData{1}. The set of all distinct labels ofValidationData{2}must be a subset of all distinct labels ofY. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, if you do not specify the network architecture using the
Networkargument, you can specifyValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify ValidationData and want to display the
validation loss at the command line, set Verbose to
1.
Number of iterations between validation evaluations, specified as a positive integer scalar. A value of 1 indicates to evaluate validation metrics at every iteration.
Note
To use this name-value argument, you must specify
ValidationData.
Example: ValidationFrequency=5
Data Types: single | double
Stopping condition for validation evaluations, specified as a nonnegative integer
scalar. The training process stops if the validation loss is greater than or equal to
the minimum validation loss computed so far, ValidationPatience
times in a row. You can check the Mdl.TrainingHistory table to see
the running total of times that the validation loss is greater than or equal to the
minimum (Validation Checks).
Example: ValidationPatience=10
Data Types: single | double
Other Classification Options
Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the
predictor data is in a table (Tbl), fitcnet
assumes that a variable is categorical if it is a logical vector, categorical vector, character
array, string array, or cell array of character vectors. If the predictor data is a matrix
(X), fitcnet assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
For the identified categorical predictors, fitcnet creates
dummy variables using two different schemes, depending on whether a categorical variable
is unordered or ordered. For an unordered categorical variable,
fitcnet creates one dummy variable for each level of the
categorical variable. For an ordered categorical variable,
fitcnet creates one less dummy variable than the number of
categories. For details, see Automatic Creation of Dummy Variables.
Example: CategoricalPredictors="all"
Data Types: single | double | logical | char | string | cell
Names of classes to use for training, specified as a categorical, character, or string
array; a logical or numeric vector; or a cell array of character vectors.
ClassNames must have the same data type as the response variable
in Tbl or Y.
If ClassNames is a character array, then each element must correspond to one row of the array.
Use ClassNames to:
Specify the order of the classes during training.
Specify the order of any input or output argument dimension that corresponds to the class order. For example, use
ClassNamesto specify the order of the dimensions ofCostor the column order of classification scores returned bypredict.Select a subset of classes for training. For example, suppose that the set of all distinct class names in
Yis["a","b","c"]. To train the model using observations from classes"a"and"c"only, specifyClassNames=["a","c"].
The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.
Example: ClassNames=["b","g"]
Data Types: categorical | char | string | logical | single | double | cell
Since R2023a
Misclassification cost, specified as a square matrix or structure array.
If you specify a square matrix
Costand the true class of an observation isi, thenCost(i,j)is the cost of classifying a point into classj. That is, rows correspond to the true classes, and columns correspond to the predicted classes. To specify the class order for the corresponding rows and columns ofCost, also set theClassNamesname-value argument.If you specify a structure
S, then it must have two fields:S.ClassNames, which contains the class names as a variable of the same data type asYS.ClassificationCosts, which contains the cost matrix with rows and columns ordered as inS.ClassNames
The default value for Cost is ones(K) –
eye(K), where K is the number of distinct
classes.
Example: Cost=[0 1; 2 0]
Data Types: single | double | struct
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the predictor order inX. Assuming thatXhas the default orientation, with observations in rows and predictors in columns,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitcnetuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Since R2023a
Prior class probabilities, specified as a value in this table.
| Value | Description |
|---|---|
"empirical" | The class prior probabilities are the class relative frequencies in
Y. |
"uniform" | All class prior probabilities are equal to 1/K, where K is the number of classes. |
| numeric vector | Each element is a class prior probability. Order the elements according
to Mdl.ClassNames or specify the
order using the ClassNames name-value argument. The
software normalizes the elements to sum to 1. |
| structure | A structure
|
If you specify the neural network architecture using the Network
argument, then Prior must be
"empirical".
Example: Prior=struct(ClassNames=["b","g"],ClassProbs=1:2)
Data Types: single | double | char | string | struct
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Score transformation, specified as a character vector, string scalar, or function handle.
This table summarizes the available character vectors and string scalars.
| Value | Description |
|---|---|
"doublelogit" | 1/(1 + e–2x) |
"invlogit" | log(x / (1 – x)) |
"ismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 |
"logit" | 1/(1 + e–x) |
"none" or "identity" | x (no transformation) |
"sign" | –1 for x < 0 0 for x = 0 1 for x > 0 |
"symmetric" | 2x – 1 |
"symmetricismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 |
"symmetriclogit" | 2/(1 + e–x) – 1 |
For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).
Example: ScoreTransform="logit"
Data Types: char | string | function_handle
Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.
If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as 'W'. Otherwise, the software treats all columns of Tbl, including W, as predictors or the response variable when training the model.
By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.
Inf weights are not supported. If you specify the neural network architecture using the Network
argument, then Weights must be a vector of ones.
Data Types: single | double | char | string
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparameters name-value argument. You can modify the
cross-validation for OptimizeHyperparameters only by using the
HyperparameterOptimizationOptions name-value argument.
Cross-Validation Options
Flag to train a cross-validated classifier, specified as "on"
or "off".
If you specify "on", then the software trains a cross-validated
classifier with 10 folds.
You can override this cross-validation setting using the
CVPartition, Holdout,
KFold, or Leaveout name-value argument.
You can use only one cross-validation name-value argument at a time to create a
cross-validated model.
Alternatively, cross-validate later by passing Mdl to
crossval.
Example: Crossval="on"
Data Types: char | string
Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the
indexing for the training and validation sets.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Suppose you create a random partition for 5-fold cross-validation on 500
observations by using cvp = cvpartition(500,KFold=5). Then, you can
specify the cross-validation partition by setting
CVPartition=cvp.
Fraction of the data used for holdout validation, specified as a scalar value in the range
(0,1). If you specify Holdout=p, then the software completes these
steps:
Randomly select and reserve
p*100% of the data as validation data, and train the model using the rest of the data.Store the compact trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Holdout=0.1
Data Types: double | single
Number of folds to use in the cross-validated model, specified as a positive integer value
greater than 1. If you specify KFold=k, then the software completes
these steps:
Randomly partition the data into
ksets.For each set, reserve the set as validation data, and train the model using the other
k– 1 sets.Store the
kcompact trained models in ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: KFold=5
Data Types: single | double
Leave-one-out cross-validation flag, specified as "on" or
"off". If you specify Leaveout="on", then for
each of the n observations (where n is the number
of observations, excluding missing observations, specified in the
NumObservations property of the model), the software completes
these steps:
Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Leaveout="on"
Data Types: char | string
Hyperparameter Optimization Options
Parameters to optimize, specified as one of the following:
"none"— Do not optimize."auto"— Use["Activations","Lambda","LayerSizes","Standardize"]."all"— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
The optimization attempts to minimize the cross-validation loss
(error) for fitcnet by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitcnet to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
To optimize the model hyperparameters, the Network
argument must be []. The eligible parameters for
fitcnet are:
Activations—fitcnetoptimizesActivationsover the set["relu","tanh","sigmoid","none"].Lambda—fitcnetoptimizesLambdaover continuous values in the range[1e-5,1e5]/NumObservations, where the value is chosen uniformly in the log transformed range.LayerBiasesInitializer—fitcnetoptimizesLayerBiasesInitializerover the two values["zeros","ones"].LayerWeightsInitializer—fitcnetoptimizesLayerWeightsInitializerover the two values["glorot","he"].LayerSizes—fitcnetoptimizes over the three values1,2, and3fully connected layers, excluding the final fully connected layer.fitcnetoptimizes each fully connected layer separately over1through300sizes in the layer, sampled on a logarithmic scale.Note
When you use the
LayerSizesargument, the iterative display shows the size of each relevant layer. For example, if the current number of fully connected layers is3, and the three layers are of sizes10,79, and44respectively, the iterative display showsLayerSizesfor that iteration as[10 79 44].Note
To access up to five fully connected layers or a different range of sizes in a layer, use
hyperparametersto select the optimizable parameters and ranges.Standardize—fitcnetoptimizesStandardizeover the two values[true,false].
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault values. As an
example, this code sets the range of NumLayers to [1
5] and optimizes Layer_4_Size and
Layer_5_Size:
load fisheriris params = hyperparameters("fitcnet",meas,species); params(1).Range = [1 5]; params(10).Optimize = true; params(11).Optimize = true;
Pass params as the value of
OptimizeHyperparameters. For an example using nondefault
parameters, see Customize Neural Network Classifier Optimization.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is the misclassification rate. To control the
iterative display, set the Verbose option of the
HyperparameterOptimizationOptions name-value argument. To control the
plots, set the ShowPlots field of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Improve Neural Network Classifier Using OptimizeHyperparameters.
Example: OptimizeHyperparameters="auto"
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you must
also specify OptimizeHyperparameters. All the options are optional.
However, you must set ConstraintBounds and
ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Output Arguments
Trained neural network classifier, returned as a ClassificationNeuralNetwork or ClassificationPartitionedModel model object.
If you set any of the name-value arguments CrossVal,
CVPartition, Holdout,
KFold, or Leaveout, then
Mdl is a ClassificationPartitionedModel model
object. Otherwise, Mdl is a
ClassificationNeuralNetwork model object.
To reference properties of Mdl, use dot notation.
If you specify OptimizeHyperparameters and
set the ConstraintType and ConstraintBounds options of
HyperparameterOptimizationOptions, then Mdl is an
N-by-1 cell array of model objects, where N is equal
to the number of rows in ConstraintBounds. If none of the optimization
problems yields a feasible model, then each cell array value is [].
If you fit the model with the Network argument set to a layer array or dlnetwork object, then to examine the neural network architecture of the model, convert the model to a dlnetwork object using the dlnetwork (Deep Learning Toolbox) function.
Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. For an example that
shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
More About
The default neural network classifier has the following layer structure.
| Structure | Description |
|---|---|
|
| Input — This layer corresponds to the predictor data in
Tbl or X. |
First fully connected layer — This layer has 10 outputs by default.
| |
ReLU activation function —
| |
Final fully connected layer — This layer has K outputs, where K is the number of classes in the response variable.
| |
Softmax function (for both binary and multiclass classification) —
The results correspond to the predicted classification scores (or posterior probabilities). | |
| Output — This layer corresponds to the predicted class labels. |
For an example that shows how a neural network classifier with this layer structure returns predictions, see Predict Using Layer Structure of Neural Network Classifier.
To specify a custom neural network architecture, use the
Network
argument. (since R2025a)
Tips
Always try to standardize the numeric predictors (see
Standardize). Standardization makes predictors insensitive to the scales on which they are measured.After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
fitcnet uses a limited-memory Broyden-Fletcher-Goldfarb-Shanno
quasi-Newton algorithm (LBFGS) [3] as its loss function
minimization technique, where the software minimizes the cross-entropy loss. The LBFGS
solver uses a standard line-search method with an approximation to the Hessian.
If you specify the
Cost,Prior, andWeightsname-value arguments, the output model object stores the specified values in theCost,Prior, andWproperties, respectively. TheCostproperty stores the user-specified cost matrix as is. ThePriorandWproperties store the prior probabilities and observation weights, respectively, after normalization. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.The software uses the
Costproperty for prediction, but not training. Therefore,Costis not read-only; you can change the property value by using dot notation after creating the trained model.
References
[1] Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pp. 249–256. 2010.
[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification.” In Proceedings of the IEEE international conference on computer vision, pp. 1026–1034. 2015.
[3] Nocedal, J. and S. J. Wright. Numerical Optimization, 2nd ed., New York: Springer, 2006.
Extended Capabilities
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitcnet function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
fitcnetfits the model on a GPU if one of the following applies:The input argument
Xis agpuArrayobject.The input argument
TblcontainsgpuArraypredictor variables.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2021afitcnet defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
fitcnet now supports GPU arrays.
fitcnet supports misclassification costs and prior probabilities for
neural network classifiers. Specify the Cost and
Prior name-value arguments when you create a model. Alternatively,
you can specify misclassification costs after training a model by using dot notation to
change the Cost property value of the
model.
Mdl.Cost = [0 2; 1 0];
See Also
ClassificationNeuralNetwork | predict | loss | hyperparameters | margin | edge | ClassificationPartitionedModel | CompactClassificationNeuralNetwork | dlnetwork (Deep Learning Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)