selectFeatures

Select important features for NCA classification or regression

Since R2023b

Syntax

idx = selectFeatures(mdl)

idx = selectFeatures(mdl,NumFeatures=numfeatures)

idx = selectFeatures(mdl,MaxWeightFraction=maxweightfraction)

Description

idx = selectFeatures(mdl) returns indices idx of selected predictors arranged in descending order of feature weights.

example

idx = selectFeatures(mdl,NumFeatures=numfeatures) returns indices of selected predictors for the number of important features specified by numfeatures.

example

idx = selectFeatures(mdl,MaxWeightFraction=maxweightfraction) returns indices of selected predictors with feature weights greater than or equal to the threshold specified by maxweightfraction.

example

Examples

collapse all

Find Important Features in Data Using NCA for Classification

Open Live Script

Generate data where the response variable depends on the 3rd, 9th, and 15th predictors.

rng(0,"twister"); % For reproducibility
N = 100;
X = rand(N,20);
y = -ones(N,1);
y(X(:,3).*X(:,9)./X(:,15) < 0.4) = 1;

Fit the NCA model for classification.

mdl = fscnca(X,y,Solver="sgd",Verbose=1);

 o Tuning initial learning rate: NumTuningIterations = 20, TuningSubsetSize = 100

|===============================================|
|    TUNING    | TUNING SUBSET |    LEARNING    |
|     ITER     |   FUN VALUE   |      RATE      |
|===============================================|
|            1 | -3.755936e-01 |   2.000000e-01 |
|            2 | -3.950971e-01 |   4.000000e-01 |
|            3 | -4.311848e-01 |   8.000000e-01 |
|            4 | -4.903195e-01 |   1.600000e+00 |
|            5 | -5.630190e-01 |   3.200000e+00 |
|            6 | -6.166993e-01 |   6.400000e+00 |
|            7 | -6.255669e-01 |   1.280000e+01 |
|            8 | -6.255669e-01 |   1.280000e+01 |
|            9 | -6.255669e-01 |   1.280000e+01 |
|           10 | -6.255669e-01 |   1.280000e+01 |
|           11 | -6.255669e-01 |   1.280000e+01 |
|           12 | -6.255669e-01 |   1.280000e+01 |
|           13 | -6.255669e-01 |   1.280000e+01 |
|           14 | -6.279210e-01 |   2.560000e+01 |
|           15 | -6.279210e-01 |   2.560000e+01 |
|           16 | -6.279210e-01 |   2.560000e+01 |
|           17 | -6.279210e-01 |   2.560000e+01 |
|           18 | -6.279210e-01 |   2.560000e+01 |
|           19 | -6.279210e-01 |   2.560000e+01 |
|           20 | -6.279210e-01 |   2.560000e+01 |

 o Solver = SGD, MiniBatchSize = 10, PassLimit = 5

|==========================================================================================|
|   PASS   |     ITER     | AVG MINIBATCH | AVG MINIBATCH |   NORM STEP   |    LEARNING    |
|          |              |   FUN VALUE   |   NORM GRAD   |               |      RATE      |
|==========================================================================================|
|        0 |            9 | -5.658450e-01 |  4.492407e-02 |  9.290605e-01 |   2.560000e+01 |
|        1 |           19 | -6.131382e-01 |  4.923625e-02 |  7.421541e-01 |   1.280000e+01 |
|        2 |           29 | -6.225056e-01 |  3.738784e-02 |  3.277588e-01 |   8.533333e+00 |
|        3 |           39 | -6.233366e-01 |  4.947901e-02 |  5.431133e-01 |   6.400000e+00 |
|        4 |           49 | -6.238576e-01 |  3.445763e-02 |  2.946188e-01 |   5.120000e+00 |

         Two norm of the final step = 2.946e-01
Relative two norm of the final step = 6.588e-02, TolX = 1.000e-06
EXIT: Iteration or pass limit reached.

Plot the selected features. The weights of the irrelevant features are close to zero.

figure()
plot(mdl.FeatureWeights,"ro")
grid on
xlabel("Feature Index")
ylabel("Feature Weight")

Figure contains an axes object. The axes object with xlabel Feature Index, ylabel Feature Weight contains a line object which displays its values using only markers.

Sort all predictors according to their feature weights.

idx = selectFeatures(mdl);
mdl.PredictorNames(idx).'

ans = 20x1 cell
    {'x15'}
    {'x3' }
    {'x9' }
    {'x16'}
    {'x10'}
    {'x13'}
    {'x2' }
    {'x18'}
    {'x17'}
    {'x12'}
    {'x14'}
    {'x8' }
    {'x4' }
    {'x11'}
    {'x19'}
    {'x20'}
    {'x6' }
    {'x5' }
    {'x7' }
    {'x1' }

mdl.FeatureWeights(idx)

Select five predictors with the largest feature weights.

idx = selectFeatures(mdl,NumFeatures=5);
mdl.PredictorNames(idx).'

ans = 5x1 cell
    {'x15'}
    {'x3' }
    {'x9' }
    {'x16'}
    {'x10'}

Select predictors with feature weights greater than or equal to the threshold defined by maxweightfraction.

idx = selectFeatures(mdl,MaxWeightFraction=0.4);
mdl.PredictorNames(idx).'

ans = 3x1 cell
    {'x15'}
    {'x3' }
    {'x9' }

Find Important Features in Data Using NCA for Regression

Open Live Script

Generate data where the response variable depends on the 3rd, 9th, and 15th predictors.

rng(0,"twister"); % For reproducibility
N = 100;
X = rand(N,20);
y = 1 + X(:,3)*5 + sin(X(:,9)./X(:,15) + 0.25*randn(N,1));

Fit the NCA model for regression.

mdl = fsrnca(X,y,Solver="lbfgs",Verbose=1,Lambda=0.5/N);

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  1.636932e+00 |   3.688e-01 |   0.000e+00 |        |   1.627e+00 |   0.000e+00 |   YES  |
|        1 |  8.304833e-01 |   1.083e-01 |   2.449e+00 |    OK  |   9.194e+00 |   4.000e+00 |   YES  |
|        2 |  7.548105e-01 |   1.341e-02 |   1.164e+00 |    OK  |   1.095e+01 |   1.000e+00 |   YES  |
|        3 |  7.346997e-01 |   9.752e-03 |   6.383e-01 |    OK  |   2.979e+01 |   1.000e+00 |   YES  |
|        4 |  7.053407e-01 |   1.605e-02 |   1.712e+00 |    OK  |   5.809e+01 |   1.000e+00 |   YES  |
|        5 |  6.970502e-01 |   9.106e-03 |   8.818e-01 |    OK  |   6.223e+01 |   1.000e+00 |   YES  |
|        6 |  6.952347e-01 |   5.522e-03 |   6.382e-01 |    OK  |   3.280e+01 |   1.000e+00 |   YES  |
|        7 |  6.946302e-01 |   9.102e-04 |   1.952e-01 |    OK  |   3.380e+01 |   1.000e+00 |   YES  |
|        8 |  6.945037e-01 |   6.557e-04 |   9.942e-02 |    OK  |   8.490e+01 |   1.000e+00 |   YES  |
|        9 |  6.943908e-01 |   1.997e-04 |   1.756e-01 |    OK  |   1.124e+02 |   1.000e+00 |   YES  |
|       10 |  6.943785e-01 |   3.478e-04 |   7.755e-02 |    OK  |   7.621e+01 |   1.000e+00 |   YES  |
|       11 |  6.943728e-01 |   1.428e-04 |   3.416e-02 |    OK  |   3.649e+01 |   1.000e+00 |   YES  |
|       12 |  6.943711e-01 |   1.128e-04 |   1.231e-02 |    OK  |   6.092e+01 |   1.000e+00 |   YES  |
|       13 |  6.943688e-01 |   1.066e-04 |   2.326e-02 |    OK  |   9.319e+01 |   1.000e+00 |   YES  |
|       14 |  6.943655e-01 |   9.324e-05 |   4.399e-02 |    OK  |   1.810e+02 |   1.000e+00 |   YES  |
|       15 |  6.943603e-01 |   1.206e-04 |   8.823e-02 |    OK  |   4.609e+02 |   1.000e+00 |   YES  |
|       16 |  6.943582e-01 |   1.701e-04 |   6.669e-02 |    OK  |   8.425e+01 |   5.000e-01 |   YES  |
|       17 |  6.943552e-01 |   5.160e-05 |   6.473e-02 |    OK  |   8.832e+01 |   1.000e+00 |   YES  |
|       18 |  6.943546e-01 |   2.477e-05 |   1.215e-02 |    OK  |   7.925e+01 |   1.000e+00 |   YES  |
|       19 |  6.943546e-01 |   1.077e-05 |   6.086e-03 |    OK  |   1.378e+02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 |  6.943545e-01 |   2.260e-05 |   4.071e-03 |    OK  |   5.856e+01 |   1.000e+00 |   YES  |
|       21 |  6.943545e-01 |   4.250e-06 |   1.109e-03 |    OK  |   2.964e+01 |   1.000e+00 |   YES  |
|       22 |  6.943545e-01 |   1.916e-06 |   8.356e-04 |    OK  |   8.649e+01 |   1.000e+00 |   YES  |
|       23 |  6.943545e-01 |   1.083e-06 |   5.270e-04 |    OK  |   1.168e+02 |   1.000e+00 |   YES  |
|       24 |  6.943545e-01 |   1.791e-06 |   2.673e-04 |    OK  |   4.016e+01 |   1.000e+00 |   YES  |
|       25 |  6.943545e-01 |   2.596e-07 |   1.111e-04 |    OK  |   3.154e+01 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 2.596e-07
              Two norm of the final step     = 1.111e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 2.596e-07, TolFun = 1.000e-06
EXIT: Local minimum found.

Plot the selected features. The weights of the irrelevant features are close to zero.

figure;
plot(mdl.FeatureWeights,"ro");
grid on;
xlabel("Feature Index");
ylabel("Feature Weight");

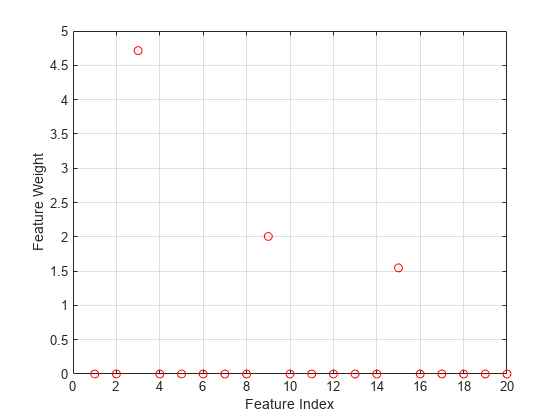
Figure contains an axes object. The axes object with xlabel Feature Index, ylabel Feature Weight contains a line object which displays its values using only markers.

Sort all predictors according to their feature weights.

idx = selectFeatures(mdl);
mdl.PredictorNames(idx).'

ans = 20x1 cell
    {'x3' }
    {'x9' }
    {'x15'}
    {'x8' }
    {'x18'}
    {'x17'}
    {'x13'}
    {'x6' }
    {'x16'}
    {'x5' }
    {'x4' }
    {'x20'}
    {'x10'}
    {'x1' }
    {'x11'}
    {'x2' }
    {'x12'}
    {'x19'}
    {'x7' }
    {'x14'}

mdl.FeatureWeights(idx)

Select five predictors with the largest feature weights.

idx = selectFeatures(mdl,NumFeatures=5);
mdl.PredictorNames(idx).'

ans = 5x1 cell
    {'x3' }
    {'x9' }
    {'x15'}
    {'x8' }
    {'x18'}

Select predictors with feature weights greater than or equal to the threshold defined by maxweightfraction.

idx = selectFeatures(mdl,MaxWeightFraction=0.4);
mdl.PredictorNames(idx).'

ans = 2x1 cell
    {'x3'}
    {'x9'}

Input Arguments

collapse all

`mdl` — Neighborhood component analysis (NCA) model for classification or regression
`FeatureSelectionNCAClassification` object | `FeatureSelectionNCARegression` object

Neighborhood component analysis (NCA) model for classification or regression, specified as a FeatureSelectionNCAClassification object or a FeatureSelectionNCARegression object.

`numfeatures` — Number of important features
number of predictors (default) | positive integer

Number of important features, specified as a positive integer.

Example: 10

Data Types: double

`maxweightfraction` — Fraction for computing threshold on feature weights
`[]` (default) | real value in the range `[0,1]`

Fraction for computing the threshold on the feature weights, specified as a real value in the range [0,1]. This value determines the threshold as follows:

threshold = maxweightfraction*max(1,max(mdl.FeatureWeights))

selectFeatures returns features with weights greater than or equal to the threshold.

Example: 0.5

Data Types: double

Output Arguments

collapse all

`idx` — Indices of selected predictors
numeric vector

Indices of selected predictors, returned as a numeric vector.

Version History

Introduced in R2023b

selectFeatures

Syntax

Description

Examples

Find Important Features in Data Using NCA for Classification

Find Important Features in Data Using NCA for Regression

Input Arguments

mdl — Neighborhood component analysis (NCA) model for classification or regression FeatureSelectionNCAClassification object | FeatureSelectionNCARegression object

numfeatures — Number of important features number of predictors (default) | positive integer

maxweightfraction — Fraction for computing threshold on feature weights [] (default) | real value in the range [0,1]

Output Arguments

idx — Indices of selected predictors numeric vector

Version History

See Also

`mdl` — Neighborhood component analysis (NCA) model for classification or regression
`FeatureSelectionNCAClassification` object | `FeatureSelectionNCARegression` object

`numfeatures` — Number of important features
number of predictors (default) | positive integer

`maxweightfraction` — Fraction for computing threshold on feature weights
`[]` (default) | real value in the range `[0,1]`

`idx` — Indices of selected predictors
numeric vector