resubPredict
Classify observations in classification tree by resubstitution
Syntax
Description
Examples
Find the total number of misclassifications of the Fisher iris data for a classification tree.
load fisheriris tree = fitctree(meas,species); Ypredict = resubPredict(tree); % The predictions Ysame = strcmp(Ypredict,species); % True when == sum(~Ysame) % How many are different?
ans = 3
Load Fisher's iris data set. Partition the data into training (50%)
load fisheririsGrow a classification tree using the all petal measurements.
Mdl = fitctree(meas(:,3:4),species); n = size(meas,1); % Sample size K = numel(Mdl.ClassNames); % Number of classes
View the classification tree.
view(Mdl,'Mode','graph');
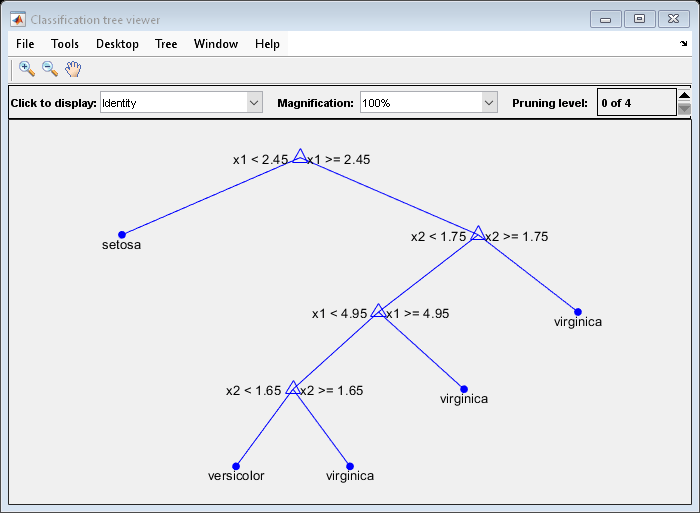
The classification tree has four pruning levels. Level 0 is the full, unpruned tree (as displayed). Level 4 is just the root node (i.e., no splits).
Estimate the posterior probabilities for each class using the subtrees pruned to levels 1 and 3.
[~,Posterior] = resubPredict(Mdl,'Subtrees',[1 3]);Posterior is an n-by- K-by- 2 array of posterior probabilities. Rows of Posterior correspond to observations, columns correspond to the classes with order Mdl.ClassNames, and pages correspond to pruning level.
Display the class posterior probabilities for iris 125 using each subtree.
Posterior(125,:,:)
ans =
ans(:,:,1) =
0 0.0217 0.9783
ans(:,:,2) =
0 0.5000 0.5000
The decision stump (page 2 of Posterior) has trouble predicting whether iris 125 is versicolor or virginica.
Classify a predictor X as true when X < 0.15 or X > 0.95, and as false otherwise.
Generate 100 uniformly distributed random numbers between 0 and 1, and classify them using a tree model.
rng("default") % For reproducibility X = rand(100,1); Y = (abs(X - 0.55) > 0.4); tree = fitctree(X,Y); view(tree,"Mode","graph")

Prune the tree.
tree1 = prune(tree,"Level",1); view(tree1,"Mode","graph")

The pruned tree correctly classifies observations that are less than 0.15 as true. It also correctly classifies observations from 0.15 to 0.95 as false. However, it incorrectly classifies observations that are greater than 0.95 as false. Therefore, the score for observations that are greater than 0.15 should be about 0.05/0.85=0.06 for true, and about 0.8/0.85=0.94 for false.
Compute the prediction scores (posterior probabilities) for the first 10 rows of X.
[~,score] = resubPredict(tree1); [score(1:10,:) X(1:10)]
ans = 10×3
0.9059 0.0941 0.8147
0.9059 0.0941 0.9058
0 1.0000 0.1270
0.9059 0.0941 0.9134
0.9059 0.0941 0.6324
0 1.0000 0.0975
0.9059 0.0941 0.2785
0.9059 0.0941 0.5469
0.9059 0.0941 0.9575
0.9059 0.0941 0.9649
Indeed, every value of X (the right-most column) that is less than 0.15 has associated scores (the left and center columns) of 0 and 1, while the other values of X have associated scores of approximately 0.91 and 0.09. The difference (score of 0.09 instead of the expected 0.06) is due to a statistical fluctuation: there are 8 observations in X in the range (0.95,1) instead of the expected 5 observations.
sum(X > 0.95)
ans = 8
Input Arguments
Classification tree model, specified as a ClassificationTree model object trained with fitctree.
Pruning level, specified as a vector of nonnegative integers in ascending order or
"all".
If you specify a vector, then all elements must be at least 0 and
at most max(tree.PruneList). 0 indicates the full,
unpruned tree, and max(tree.PruneList) indicates the completely
pruned tree (that is, just the root node).
If you specify "all", then resubPredict
operates on all subtrees (that is, the entire pruning sequence). This specification is
equivalent to using 0:max(tree.PruneList).
resubPredict prunes tree to each level
specified by subtrees, and then estimates the corresponding output
arguments. The size of subtrees determines the size of some output
arguments.
For the function to invoke subtrees, the properties
PruneList and PruneAlpha of
tree must be nonempty. In other words, grow
tree by setting Prune="on" when you use
fitctree, or by pruning tree using prune.
Data Types: single | double | char | string
Output Arguments
Predicted class labels for the training data, returned as a categorical or character
array, logical or numeric vector, or cell array of character vectors.
label has the same data type as the training response data
tree.Y.
If subtrees contains m >
1 entries, then label is returned as a matrix
with m columns, each of which represents the predictions of the
corresponding subtree. Otherwise, label is returned as a
vector.
Posterior probabilities for the classes predicted by tree,
returned as a numeric matrix or numeric array.
If subtrees is a scalar or is not specified, then
resubPredict returns posterior as an
n-by-k numeric matrix, where
n is the number of rows in the training data
tree.X, and k is the number of classes.
If subtrees contains m >
1 entries, then resubPredict returns
posterior as an
n-by-k-by-m numeric array,
where the matrix for each m gives posterior probabilities for the
corresponding subtree.
Node numbers for the predicted classes, returned as a numeric column vector or numeric matrix.
If subtrees is a scalar or is not specified, then
resubPredict returns node as a numeric column
vector with n rows, the same number of rows as
tree.X.
If subtrees contains m > 1
entries, then node is an n-by-m
numeric matrix. Each column represents the node predictions of the corresponding
subtree.
Predicted class numbers for resubstituted data, returned as a numeric column vector or numeric matrix.
If subtrees is a scalar or is not specified, then
cnum is a numeric column vector with n rows,
the same number of rows as tree.X.
If subtrees contains m >
1 entries, then cnum is an
n-by-m numeric matrix. Each column represents
the class predictions of the corresponding subtree.
More About
The posterior probability of the classification at a node is the number of training sequences that lead to that node with this classification, divided by the number of training sequences that lead to that node.
For an example, see Posterior Probability Definition for Classification Tree.
Extended Capabilities
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011a
See Also
resubEdge | resubMargin | resubLoss | predict | fitctree | ClassificationTree
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)