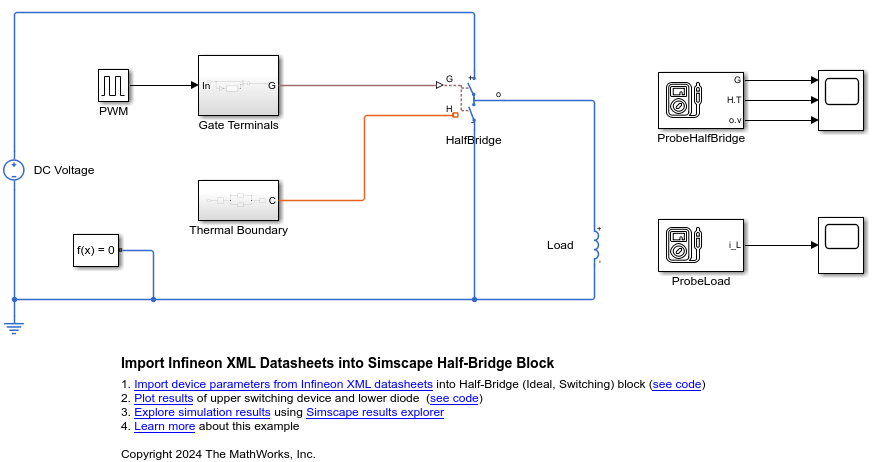
Half-Bridge (Ideal, Switching)
Libraries:
Simscape /
Electrical /
Semiconductors & Converters
Description
The Half-Bridge (Ideal, Switching) block models a half-bridge
with ideal switches and a thermal port. To choose the ideal switching device, set the
Switching device parameter to
MOSFET, IGBT, or
GTO.
You can specify an integral protection diode for each switching device. An integral diode protects the semiconductor device by providing a conduction path for a reverse current. An inductive load can produce a high reverse-voltage spike when the semiconductor device suddenly switches off the voltage supply to the load.
Note
The best option is to model diodes internally within the Half-Bridge (Ideal, Switching) block. To model the diodes externally, model them without capacitance or charge.
Switching Losses
For information about how the block models turn-on and turn-off losses, see the
documentation page for the MOSFET (Ideal, Switching) block, IGBT (Ideal, Switching) block, or GTO block, depending on the option you select for the
Switching Device parameter. The main difference between how
these blocks and the Half-Bridge (Ideal, Switching)
block model the losses is that, for the MOSFET and
IGBT options, the Half-Bridge (Ideal,
Switching) block does not use the Use last on-state
current from previous cycle for turn-on loss or Use last
off-state voltage from previous cycle for turn-off loss parameters.
The reason for this difference is that the Half-Bridge (Ideal,
Switching) block does not model diode capacitance or lead
inductance because the block is designed for fast simulation using ideal switching.
By modeling both switching devices in one block, you avoid the complexities
associated with measuring the on-state current and off-state voltage for diode
reverse recovery, so you do not need a physics-based diode charge model. The block
measures the diode forward current and off-state voltages at the point that you
command the complementary switching device to switch off.
By default, the block applies switching losses to the thermal node only, stepping the node temperature up by the requisite value. To draw the requisite power due to switching losses from the electrical supply, select the Apply switching losses to electrical supply parameter.
Instantaneously applying a switching loss to the electrical supply is not mathematically possible, so the block applies switching losses over a period equal to the value you specify for the Averaging period for switching losses parameter. Set this value equal to the pulse-width modulation (PWM) period of the gate driver.
Note
For all ideal switching devices, the logged simulation data reports the
thermal losses as lastTurnOffLoss,
lastTurnOnLoss, and
lastReverseRecoveryLoss. These variables include losses
as a pulse with an amplitude equal to the energy loss. If you use a script to
sum the total losses over a defined simulation period, you must sum the pulse
values at each pulse rising edge. Alternatively, you can extract conduction and
switching losses from logged data using the ee_getPowerLossSummary and
ee_getPowerLossTimeSeries functions.
To learn how to log and plot simulation data, see the Log and Plot Simulation Data example.
You can also access the total accumulated switching losses for each of the two
switching devices from the respective
accumulatedSwitchingLosses variables in the logged
simulation data. These variables sum all switching losses to date, including
reverse recovery losses for the diode.
The power_dissipated variable in the logged simulation data
does not include switching losses because the block models these losses as
instantaneous events. The power_dissipated variable reports
ohmic on-state losses.
If you are using a fixed-step solver, the shortest pulse on or pulse off that supports capture of the switching losses is three time steps long. If the pulse is shorter than three steps, the block does not report switching losses.
If you use tabulated data to model the switching losses or reverse recovery losses, check that the temperature, current, and voltage are in the range you specify. If you do not define a realistic thermal model, for example, if the junction mass or the conductance from the junction to the case is too small, the temperature can exceed the range you specify, causing the block to extrapolate the losses to nonphysical values.
Parameterization
The Half-Bridge (Ideal, Switching) block supports multiple predefined parameterizations.
Use this parameterization data to represent components by specific suppliers. The parameterizations of these half-bridges match the manufacturer data sheets. To load a predefined parameterization, double-click the Half-Bridge (Ideal, Switching) block, click the <click to select> hyperlink of the Selected part parameter, and, in the Block Parameterization Manager window, select the part you want to use from the list of available components.
Note
The predefined parameterizations of Simscape™ components use available data sources for the parameter values. Engineering judgment and simplifying assumptions are used to fill in for missing data. As a result, expect deviations between simulated and actual physical behavior. To ensure accuracy, validate the simulated behavior against experimental data and refine component models as necessary.
For more information about predefined parameterization and a list of the available components, see List of Pre-Parameterized Components.
You can also use the ee_importDeviceParameters function to extract the device parameters
for the switching device and integral protection diode from XML files and import
them into the block. The XML file must be on the MATLAB® path and must use a parameterization format supported by Hitachi or
Infineon®.
Thermal Port
Use the thermal port to simulate the effects of generated heat and device temperature. For more information on using thermal ports and the Thermal Port parameters, see Simulating Thermal Effects in Semiconductors.
You can also separate the thermal port H into two different thermal ports associated with the upper and lower switching devices, respectively, by selecting the Separate thermal ports for upper and lower devices parameter. If you separate the thermal ports for the upper and lower devices, you can then also separate the thermal ports for the integral diodes of each switching device by selecting the Separate thermal ports for integral diodes parameter. The upper and lower switching devices share the same thermal parameters. (since R2024a)
This figure shows the block icon when you expose all the thermal ports:
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Import Infineon XML Datasheets into Simscape Half-Bridge Block
Import device parameters from Infineon® datasheets for IGBTs and diodes into a Half-Bridge (Ideal, Switching) block.
Limitations
If you set the Switching device parameter to
GTO, the block assumes that the current change in the load between PWM cycles is small. This assumption implies that the load inductance or the switching frequency is large enough to smooth the current.If you select the Apply switching losses to electrical supply parameter, you must connect a power supply to the half-bridge. For example, you must clear the Apply switching losses to electrical supply parameter if your model has a switch that can disconnect one or both of the power supply connections. You can also encounter numerical initialization issues if the power supply does not initialize in the on state, for example, because of a smoothing capacitor that starts at zero charge.
