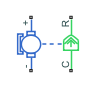
DC Motor

DC motor model with electrical and torque characteristics and fault modeling

• 

Libraries:
Simscape / Electrical / Electromechanical / Brushed Motors

Description

The DC Motor block represents the electrical and torque characteristics of a DC motor using this equivalent circuit model.

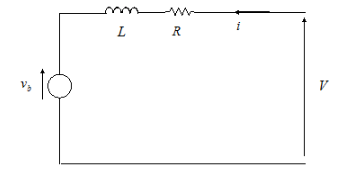
You specify the equivalent circuit parameters for this model when you set the Model parameterization parameter to By equivalent circuit parameters. The resistor R corresponds to the resistance you specify in the Armature resistance parameter. The inductor L corresponds to the inductance you specify in the Armature inductance parameter.

You can specify how to generate the magnetic field of the DC motor by setting the Field type parameter to the desired option. The permanent magnets in the motor induce the following back emf v_b in the armature:

$$v_b=k_v\omega$$

where k_v is the Back-emf constant and ω is the angular velocity. The motor produces the following torque, which is proportional to the motor current i:

$$T_E=k_{t}i$$

where k_t is the Torque constant. The DC Motor block assumes that there are no electromagnetic losses. This means that mechanical power is equal to the electrical power dissipated by the back emf in the armature. Equating these two terms gives:

$$\begin{array}{l}{T}_E\omega =v_{b}i\\ k_{t}i\omega =k_v\omega i\\ k_v=k_t\end{array}$$

As a result, you specify either k_v or k_t in the block parameters.

If the magnetic field is generated from the current flowing through the windings, the Back-emf constant depends on the field current I_f:

$$k_v=L_{af}{I}_f$$

where L_af is the Field-armature mutual inductance.

The torque-speed characteristic for the DC Motor block is related to the parameters in the preceding figure. When you set the Model parameterization parameter to By stall torque & no-load speed or By rated load and speed, the block solves for the equivalent circuit parameters as follows:

1. For the steady-state torque-speed relationship, L has no effect.

2. Sum the voltages around the loop and rearrange for i:

   $$i=\frac{V-v_b}{R}=\frac{V-k_v\omega }{R}$$

3. Substitute this value of i into the equation for torque:

   $$T_E=\frac{k_t}{R}\left(V-k_v\omega \right)$$

   When you set the Model parameterization parameter to By stall torque & no-load speed, the block uses the stall torque and no-load speed to determine values for R and k_t (and equivalently k_v).

   When you set the Model parameterization parameter to By rated load and speed, the block uses the rated speed and power to calculate the rated torque. The block uses the rated torque and no-load speed values to determine values for R and k_t.

The block models motor inertia J and damping λ for all values of the Model parameterization parameter. The resulting torque across the block is:

$$T=\frac{k_t}{R}\left(V-k_v\omega \right)-J\dot{\omega }-\lambda \omega$$

It is not always possible to measure rotor damping, and rotor damping is not always provided on a manufacturer datasheet. An alternative is to use the no-load current to infer a value for rotor damping.

For no-load, the electrically-generated mechanical torque must equal the rotor damping torque:

$$k_t{i}_{noload}=\lambda {\omega }_{noload}$$

where i_noload is the no-load current. If you select By no-load current for the Rotor damping parameterization parameter, then this equation is used in addition to the torque-speed equation to determine values for λ and the other equation coefficients.

The value for rotor damping, whether specified directly or in terms of no-load current, is taken into account when determining equivalent circuit parameters for Model parameterization options By stall torque and no-load speed and By rated load and speed.

When a positive current flows from the electrical + to - ports, a positive torque acts from the mechanical C to R ports.

Note

Simscape™ Electrical™ includes several blocks that can model the same type of motor or actuator. Choose a block that has sufficient modeling detail for the engineering design questions that you need to answer. Do not use a block that has more modeling detail than you need, because higher-fidelity models slow down simulation and are more complex to parameterize.

Blocks like the DC Motor block model motors with fixed or parameter-dependent coefficients with a simple equivalent circuit. These models have an intermediate level of fidelity. Use this block to design controls or systems in actuation applications, such as robotics and mechatronics, and for efficiency predictions when saturation and harmonics only weakly impact losses. For more information about choosing the right block to model your motor at the right level of fidelity, see Choose Blocks to Model Motors or Actuators.

Faults

To model a fault in the DC Motor block, in the Faults section, click Add fault next to the fault that you want to model. For more information about fault modeling, see Fault Behavior Modeling and Fault Triggering.

The DC Motor block allows you to model two types of faults:

• Armature winding fault — The armature winding fails and goes open circuit.

• Field winding fault — The field winding that creates the magnetic field fails and goes open circuit.

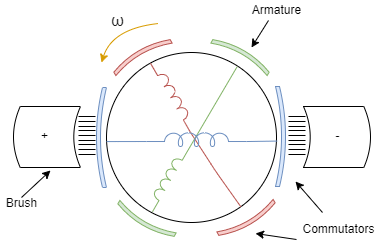
This figure shows a generic representation of a DC motor, with brushes, armatures, commutators, and their windings:

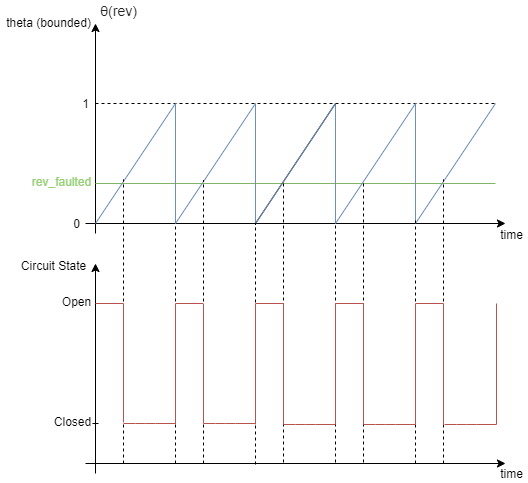
When the armature fails, the voltage source connected to this block observes an open circuit for a fraction of the total motor revolution, specified by the Fraction of revolution during which armature is open-circuit parameter, rev_faulted. This figure illustrates the circuit state behavior for a certain rev_faulted during the entire revolution period:

Fault Triggers

You specify how and when faults occur by using the Trigger type parameter.

If you set the Trigger type to Behavioral, the DC Motor block triggers faults when the winding currents continuously exceed a threshold value for longer than a specific time interval:

• Armature winding faults occur when the winding currents continuously exceed the value of the Maximum permissible armature winding current parameter for a duration longer than the value of the Time to fail when exceeding armature winding current parameter.

• Field winding faults occur when the winding currents exceed the value of the Maximum permissible field winding current parameter for a duration longer than the value of the Time to fail when exceeding field winding current parameter.

If you set the Trigger type to Conditional, you can choose whether faults in the DC Motor block are reversible (since R2025a). To model irreversible faults, click Open fault properties to open the Property Inspector and select the Trigger stays on once activated parameter. The block enters the faulted state when the trigger condition becomes true for the first time and remains in the faulted state for the rest of the simulation. To model reversible faults, clear the Trigger stays on once activated parameter. The block enters the faulted state when the trigger condition is true and enters the unfaulted state when the trigger condition is false.

For more information about adding faults to blocks and specifying fault triggers, see Introduction to Simscape Faults.

Predefined Parameterization

There are multiple available built-in parameterizations for the permanent magnet DC Motor block. To select a parameterization, set the Model Parameterization parameter to By equivalent circuit parameters.

This pre-parameterization data allows you to set up the block to represent components by specific suppliers. The parameterizations of these DC motors match the manufacturer data sheets. To load a predefined parameterization, double-click the DC Motor block, click the <click to select> hyperlink of the Selected part parameter and, in the Block Parameterization Manager window, select the part you want to use from the list of available components.

Note

The predefined parameterizations of Simscape components use available data sources for the parameter values. Engineering judgment and simplifying assumptions are used to fill in for missing data. As a result, expect deviations between simulated and actual physical behavior. To ensure accuracy, validate the simulated behavior against experimental data and refine component models as necessary.

For more information about pre-parameterization and for a list of the available components, see List of Pre-Parameterized Components.

Model Thermal Effects

You can expose the thermal port to model the effects of losses that convert power to heat. To expose the thermal port, set the Modeling option parameter to either:

• No thermal port — The block does not contain a thermal port.

• Show thermal port — The block contains one thermal conserving port.

For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.

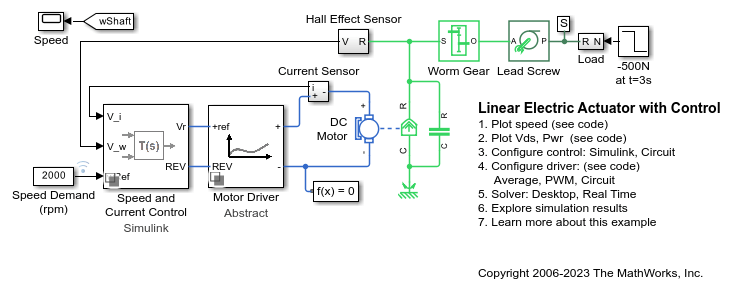
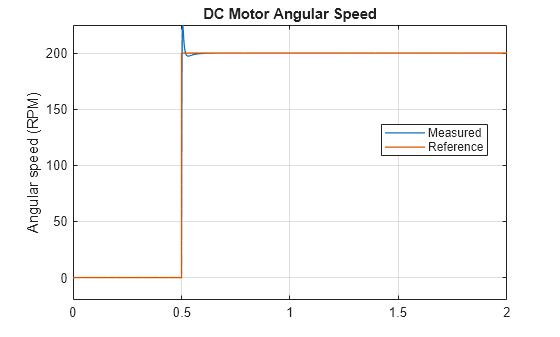
Examples

Linear Electric Actuator (Motor Model)

How to develop a model of an uncontrolled linear actuator using datasheet parameter values. The actuator consists of a DC motor driving a 6.25:1 worm gear which in turn drives a 3mm lead screw to produce linear motion. Manufacturer data for the actuator defines the no-load linear speed (26mm/s), rated load (1000N), rated-load linear speed (19mm/s), and maximum current (5A). The maximum static force is 4000N and the rated voltage is 24V DC.

• Open Model

Linear Electric Actuator with Control

A detailed implementation model of a controlled linear actuator. The actuator consists of a DC motor driving a worm gear which in turn drives a lead screw to produce linear motion. The model includes quantization effects of the Hall-effect sensor and the implementation of the control in analog electronics. There are multiple variant subsystems in this model that have models at varying levels of fidelity.

• Open Model

Control DC Motor with PWM Voltage Source and H-Bridge Driver

Control a DC motor by using the Controlled PWM Voltage and H-Bridge blocks. The DC Motor block delivers a mechanical power of 10 W at 2500 rpm and turns at a no-load speed of 4000 rpm when the DC supply voltage is 12 V. Consequently, if you set the PWM reference voltage to its maximum value of 5 V, the motor runs at 4000 rpm. If you set the PWM reference voltage to 2.5 V, the motor runs at approximately 2000 rpm. To achieve fast simulation, this example sets the Simulation mode parameter of the Controlled PWM Voltage and H-Bridge blocks to Averaged. To validate the averaged behavior, set the Simulation mode parameter to PWM in both the Controlled PWM Voltage and H-Bridge blocks.

• Open Model

Motor Torque-Speed Curves

A comparison of the torque-speed characteristics for five different motor types. To select the motor type, right-click on the Electric Motor block and select Block Parameters (Subsystem) from the context menu. In the new window, specify the desired motor using the Label mode active choice parameter. All motors have been sized for roughly the same mechanical power rating.

• Open Model

DC Motor Control

A cascade speed-control structure for a DC motor. A PWM controlled four-quadrant Chopper is used to feed the DC motor. The Control subsystem includes the outer speed-control loop, the inner current-control loop, and the PWM generation. The total simulation time (t) is 4 seconds. At t = 1.5 seconds, the load torque increases. At t = 2.5 seconds, the reference speed is changed from 1000 rpm to 2000 rpm.

• Open Model

Design PID Control for DC Motor Using Classical Control Theory

Design a PID controller for a DC Motor using classical control theory. Alternatively, you can use Steady State Manager, Model Linearizer, Frequency Response Estimator, or PID tuner apps to streamline the design.

• Since R2025a
• Open Live Script

Ports

Conserving

+ — Positive terminal

electrical

Electrical conserving port associated with the DC motor positive terminal.

- — Negative terminal

electrical

Electrical conserving port associated with the DC motor negative terminal.

C — Motor case

mechanical

Mechanical rotational conserving port associated with the DC motor case.

R — Motor rotor

mechanical

Mechanical rotational conserving port associated with the DC motor rotor.

F+ — Positive field

electrical

Electrical conserving port associated with the positive field winding.

Dependencies

To enable this port, set Field type to Wound.

F- — Negative field

electrical

Electrical conserving port associated with the negative field winding.

Dependencies

To enable this port, set Field type to Wound.

H — Thermal port

thermal

Thermal conserving port.

Dependencies

To enable this port, set Modeling option to Show thermal port.

Parameters

Modeling option — Whether to enable thermal ports

No thermal port (default) | Show thermal port

Whether to enable the thermal ports of the block and model the effects of losses that convert power to heat.

Selected part — Predefined parameterization option

<click to select> (default)

Option to parameterize the block to represent components by specific suppliers. Click the <click to select> hyperlink to open the Block Parameterization Manager window. For more information about the Block Parameterization Manager, see Load Predefined Parameterizations.

Electrical Torque

Field type — Type of field

Permanent Magnet (default) | Wound

Select one of the following methods for field type:

• Permanent Magnet — Generate the DC Motor magnetic field using a permanent magnet.

• Wound — Generate the DC Motor magnetic field using the current flowing through the windings.

Model parameterization — Block parameterization

By equivalent circuit parameters (default) | By stall torque & no-load speed | By rated load and speed

Select one of the following methods for block parameterization:

• By equivalent circuit parameters — Provide electrical parameters for an equivalent circuit model of the motor.

• By stall torque & no-load speed — Provide torque and speed parameters that the block converts to an equivalent circuit model of the motor.

• By rated load and speed — Provide power and speed parameters that the block converts to an equivalent circuit model of the motor.

Dependencies

To enable this parameter, set Field type to Permanent magnet.

Field resistance — Field resistance

100 Ohm (default)

Resistance of the magnetic field.

Dependencies

To enable this parameter, set Field type to Wound.

Field inductance — Field inductance

1 H (default)

Inductance of the magnetic field.

Dependencies

To enable this parameter, set Field type to Wound.

Field-armature mutual inductance — Field-armature mutual inductance

0.15 H (default)

Mutual inductance between the magnetic field and the conducting portion of the motor.

Dependencies

To enable this parameter, set Field type to Wound.

Initial field current — Initial field current

0 A (default)

Initial field current.

Dependencies

To enable this parameter, set Field type to Wound.

Armature resistance — Armature resistance

3.9 Ohm (default)

Resistance of the conducting portion of the motor.

Dependencies

To enable this parameter, set Model parameterization to By equivalent circuit parameters.

Armature inductance — Armature inductance

12e-6 H (default)

Inductance of the conducting portion of the motor. If you do not have information about this inductance, set the value of this parameter to a small, nonzero number.

Define back-emf or torque constant — Constants specification

Specify back-emf constant (default) | Specify torque constant

Indicate whether you will specify the motor's back-emf constant or torque constant. When you specify them in SI units, these constants have the same value, so you only specify one or the other in the block dialog box.

Dependencies

To enable this parameter, set Model parameterization to By equivalent circuit parameters.

Back-emf constant — Back-emf constant

0.072e-3 (default) | V/rpm

The ratio of the voltage generated by the motor to the speed at which the motor is spinning.

Dependencies

To enable this parameter, set Define back-emf or torque constant to Specify back-emf constant.

Torque constant — Torque constant

6.876e-4 N*m/A (default)

The ratio of the torque generated by the motor to the current delivered to it.

Dependencies

To enable this parameter, set Define back-emf or torque constant to Specify torque constant.

Stall torque — Stall torque

0.24e-3 N*m. (default)

The amount of torque generated by the motor when the speed is approximately zero.

Dependencies

To enable this parameter, set Model parameterization to By stall torque & no-load speed.

No-load speed — No-load speed

19100 rpm (default)

Speed of the motor when not driving a load.

Dependencies

To enable this parameter, set Model parameterization to By stall torque & no-load speed or By rated load and speed.

Rated speed (at rated load) — Rated speed

15000 rpm (default)

Motor speed at the rated mechanical power level.

Dependencies

To enable this parameter, set Model parameterization to By rated load and speed.

Rated load (mechanical power) — Rated load

0.08 W (default)

The mechanical power the motor is designed to deliver at the rated speed.

Dependencies

To enable this parameter, set Model parameterization to By rated load and speed.

Rated DC supply voltage — Rated DC supply voltage

1.5 V (default)

The voltage at which the motor is rated to operate.

Dependencies

To enable this parameter, set the Model parameterization to By stall torque & no-load speed or By rated load and speed.

Rotor damping parameterization — Rotor damping parameterization

By damping value (default) | By no-load current

Select one of the following methods to specify rotor damping:

• By damping value — Specify a value for rotor damping directly, by using the Rotor damping parameter in the Mechanical parameters.

• By no-load current — The block calculates rotor damping based on the values that you specify for the No-load current and DC supply voltage when measuring no-load current parameters. If you select this option, the Rotor damping parameter is not available for the Mechanical parameters.

No-load current — No-load current

0 A (default)

Specify the no-load current value, to be used for calculating the rotor damping.

Dependencies

To enable this parameter, set the Rotor damping parameterization to By no-load current.

DC supply voltage when measuring no-load current — DC supply voltage when measuring no-load current

1.5 V (default)

Specify the DC supply voltage corresponding to the no-load current value, to be used for calculating the rotor damping.

Dependencies

To enable this parameter, set the Rotor damping parameterization to By no-load current.

Mechanical

Rotor inertia — Rotor inertia

0.01 g*cm^2 (default)

Resistance of the rotor to change in motor motion. The value can be zero.

Rotor damping — Rotor dissipated energy

0 N*m/(rad/s) (default)

Energy dissipated by the rotor. The value can be zero.

Dependencies

To enable this parameter, set the Rotor damping parameterization parameter in the Electrical Torque setting to By damping value.

Initial rotor speed — Initial rotor speed

0 rpm (default)

Speed of the rotor at the start of the simulation.

Temperature Dependence

This tab appears only for blocks with exposed thermal port.

Resistance temperature coefficient — Resistance temperature coefficient

3.93e-3 1/K (default)

Resistance temperature coefficient.

Measurement temperature — Measurement temperature

25 degC (default)

The temperature for which motor parameters are defined.

Thermal Port

This tab appears only for blocks with exposed thermal port.

Thermal mass — Thermal mass

100 J/K (default)

The thermal mass is the energy required to raise the temperature by one degree.

Initial temperature — Initial temperature

25 degC (default)

Temperature of the thermal port at the start of simulation.

Faults

Armature winding fault — Option to add armature winding fault

Add fault (default)

Option to add a fault to the armature winding of the DC Motor block.

To add a fault, click the Add fault hyperlink.

Fraction of revolution during which armature is open-circuit — Fraction of revolution during which armature is open-circuit

1/3 (default)

Fraction of the revolution of the DC motor during which the armature winding is faulted and the voltage source observes an open circuit. For more information, see the Faults section.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter.

Faulted armature winding open-circuit conductance — Open-circuit conductance of faulted armature winding

1e-5 S (default)

Open-circuit conductance when the armature winding is faulted.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter.

Trigger type — Trigger type

Always on (default) | Timed | Behavioral | Additional triggers | Conditional | Manual

Trigger type, specified as one of these options:

• Always On — The fault injects at the start of the simulation.

• Timed — The fault injects when the simulation time reaches the value you specify for the Trigger fault at time parameter.

• Behavioral — The fault injects as a result of fault parameter values during simulation. Setting Trigger type to Behavioral enables block parameters that define the failure conditions.

• Additional triggers — The fault injects as a result of additional triggers not available in the block dialog box. Select this option and click the Open fault properties hyperlink to set the Trigger type to one of these values in the Property Inspector:

  • Conditional — The fault injects as a result of a condition that reflects a behavior associated with a signal. Conditionals evaluate the Boolean expression in the Condition parameter at each time step. To model irreversible faults, select the Trigger stays on once activated parameter in the Property Inspector. The block enters the faulted state when the trigger condition becomes true for the first time and remains in the faulted state for the rest of the simulation. To model reversible faults, clear the Trigger stays on once activated parameter. The block enters the faulted state when the trigger condition is true and enters the unfaulted state when the trigger condition is false. To learn more, see Create and Manage Conditionals.

  • Manual — The fault injects or clears when you toggle the status in the Fault Dashboard pane. To learn more, see Manually Trigger Faults in Models.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter.

Trigger fault at time — Time before entering faulted state

0 s (default) | nonnegative scalar

Simulation time at which the block enters the faulted state.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter and set Trigger type to Timed.

Maximum permissible armature winding current — Maximum permissible armature winding current

inf A (default)

Upper load-current threshold for open-circuit armature winding faults.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter and set Trigger type to Behavioral.

Time to fail when exceeding armature winding current — Time to fail when exceeding armature winding current

1 s (default)

Amount of time that the winding current must continuously exceed the maximum permissible armature winding current before a behavioral fault is triggered.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter and set Trigger type to Behavioral.

Trigger configuration — Option to enable additional trigger types

Open fault properties

Option to enable additional trigger types not available in the block dialog box. To set the Trigger type parameter to Conditional or Manual, click the Open fault properties hyperlink and set the Trigger type in the Property Inspector.

Dependencies

To enable this parameter, click the Add fault hyperlink for the Armature winding fault parameter and set Trigger type to Behavioral.

Field winding fault — Option to add field winding fault

Add fault (default)

Option to add a fault to the field winding of the DC Motor block.

To add a fault, click the Add fault hyperlink.

Dependencies

To enable this parameter, in the Electrical Torque settings, set Field type to Wound.

Faulted field winding open-circuit conductance — Open-circuit conductance of faulted field winding

1e-5 S (default)

Open-circuit conductance when the field winding is faulted.

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

Trigger type — Trigger type

Always on (default) | Timed | Behavioral | Additional triggers | Conditional | Manual

Trigger type, specified as one of these options:

• Always On — The fault injects at the start of the simulation.

• Timed — The fault injects when the simulation time reaches the value you specify for the Trigger fault at time parameter.

• Behavioral — The fault injects as a result of fault parameter values during simulation. Setting Trigger type to Behavioral enables block parameters that define the failure conditions.

• Additional triggers — The fault injects as a result of additional triggers not available in the block dialog box. Select this option and click the Open fault properties hyperlink to set the Trigger type to one of these values in the Property Inspector:

  • Conditional — The fault injects as a result of a condition that reflects a behavior associated with a signal. Conditionals evaluate the Boolean expression in the Condition parameter at each time step. To model irreversible faults, select the Trigger stays on once activated parameter in the Property Inspector. The block enters the faulted state when the trigger condition becomes true for the first time and remains in the faulted state for the rest of the simulation. To model reversible faults, clear the Trigger stays on once activated parameter. The block enters the faulted state when the trigger condition is true and enters the unfaulted state when the trigger condition is false. To learn more, see Create and Manage Conditionals.

  • Manual — The fault injects or clears when you toggle the status in the Fault Dashboard pane. To learn more, see Manually Trigger Faults in Models.

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

Trigger fault at time — Time before entering faulted state

0 s (default) | nonnegative scalar

Simulation time at which the block enters the faulted state.

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

• Set Trigger type to Timed.

Maximum permissible field winding current — Maximum permissible field winding current

inf A (default)

Upper load-current threshold for open-circuit field winding faults.

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

• Set Trigger type to Behavioral.

Time to fail when exceeding field winding current — Time to fail when exceeding field winding current

1 s (default)

Amount of time that the winding current must continuously exceed the maximum permissible field winding current before a behavioral fault is triggered.

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

• Set Trigger type to Behavioral.

Trigger configuration — Option to enable additional trigger types

Open fault properties

Dependencies

To enable this parameter:

• In the Electrical Torque settings, set Field type to Wound.

• Click the Add fault hyperlink for the Field winding fault parameter.

• Set Trigger type to Additional triggers.

References

[1] Bolton, W. Mechatronics: Electronic Control Systems in Mechanical and Electrical Engineering, 3rd edition Pearson Education, 2004.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2008a

R2025a: Model Reversible Conditional Faults

You can now model reversible conditional faults in the DC Motor block by clearing the Trigger stays on once activated parameter. The block enters the faulted state when the trigger condition is true and enters the unfaulted state when the trigger condition is false.

Before R2025a, the block enters the faulted state when the trigger condition becomes true for the first time and remains in the faulted state for the rest of the simulation.

If you create a model before R2025a and enable a conditional fault in the DC Motor block, the block now selects the Trigger stays on once activated parameter by default for backward compatibility.