Model Stick-Slip Friction and Hard Stops in Mass-Spring-Damper System
This example shows one way you can incorporate hard stops and friction changes from stick-slip motion into a mass-spring-damper model.
In a mass-spring-damper model, a mass attaches to the end of a spring. The spring has a nominal length that can stretch and compress in response to external forces. The spring constant determines the force the spring exerts on the mass based on how much the spring is stretched or compressed.
When the system limits the position of the mass, those limits represent hard stops in the oscillations of the mass on the spring. When the mass reaches the upper or lower bound on its position, the mass stops hard, meaning the velocity goes to 0.
Stick-slip motion can occur when two surfaces move against each other dynamically. For example, in the mass-spring-damper system, the mass moves over a surface as it oscillates on the spring. The friction between the mass and the surface changes when the velocity of the mass reaches 0. The mass sticks when the static friction is larger than the force from the spring and slips back into the oscillation when the force from the spring exceeds the static friction.
Open and Analyze Model
Open the model sldemo_hardstop. The model contains a subsystem named Friction Model that calculates the force due to friction and two Integrator blocks that compute the velocity and the position of the mass.
mdl = "sldemo_hardstop";
open_system(mdl)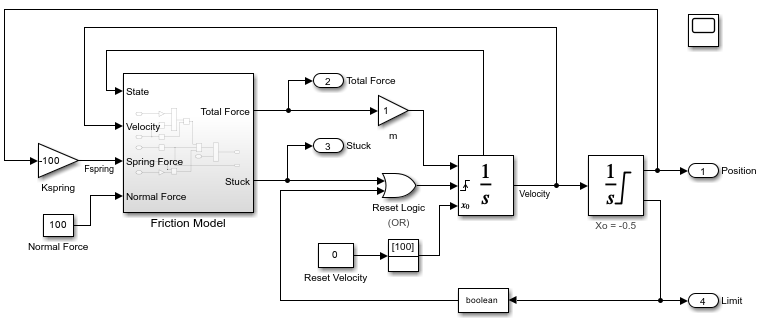
The Integrator block that computes the velocity is configured to:
Provide the state value as an output.
Reset the output value to 0 m/s based on an external signal.
Have an initial state of 100 m/s.
The Integrator block that computes the position models the hard stops in the system by limiting the output value range based on the minimum and maximum possible positions. The block has an additional output port with a signal that indicates when the output value hits one of the limits, meaning that the mass has reached the minimum or maximum position. To model the hard stop, the limit signal resets the Integrator block that computes the velocity to a velocity of 0 m/s.
View and Analyze Friction Model
To view the contents of the subsystem named Friction Model, double-click the subsystem block or use the open_system function.
open_system(mdl + "/Friction Model")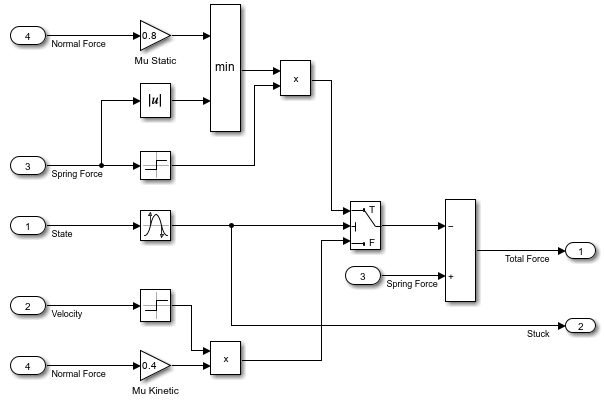
The subsystem computes two outputs: the total force that acts on the mass, and a flag that indicates when the mass sticks and has a velocity of zero.
To determine when the mass has a velocity of zero, the subsystem uses the state of the Integrator block that computes the velocity of the mass. The state of the Integrator block is the velocity from the previous major time hit in the simulation. On the major time hit after the velocity reaches zero, the friction model:
Sets the
Stuckflag, which resets the Integrator block that computes the velocitySwitches the friction computation to use the static coefficient of friction instead of the kinetic coefficient of friction
To compute the total force acting on the mass, the subsystem adds the force of the spring to the force from either kinetic or static friction.
When you use the state port of the Integrator block that computes the velocity to determine when the mass is stuck, you avoid creating an algebraic loop in the model.
Simulate Model and Analyze Results
Simulate the model. In the Simulink® Toolstrip, on the Simulation tab, click Run. Alternatively, run the simulation using the sim function.
out = sim(mdl);
Double-click the Floating Scope block to view the simulation results.
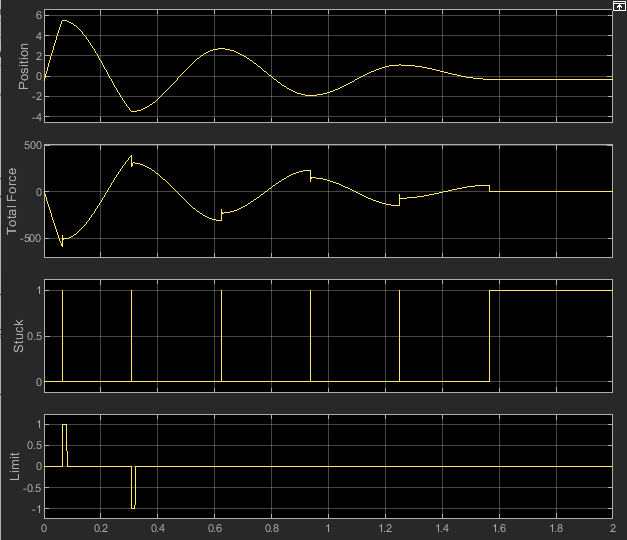
The decrease in the minima and maxima of the position signal in the top plot illustrate the way that the friction consumes energy in the system.
The discontinuities in the value of the total force shown in the second subplot show the effect of using the coefficient of static friction when the mass sticks and its velocity goes to zero.
The third subplot shows that the time hits with discontinuities correspond to time hits when the
Stuckflag was set. TheStuckflag remains set after a simulation time close to 1.6 seconds because the mass has come to rest.The last subplot shows that a hard stop occurred only twice, at the beginning of the simulation.