Generalize Memory Polynomial Power Amplifier Model Fitting
This example shows you how to:
Identify the power amplifier (PA) model coefficients matrix using the characterization waveform with the largest dynamic range and then verify the quality of the fitted model using the other waveforms.
Experiment by changing the harmonic order and memory depth of the model. Use grid-search algorithms for optimal model identification.
Determine PA Model Coefficient Matrix From Measured Input/Output Signals
Identify a generalized memory polynomial model, using a memory length of five and a degree of nonlinearity of three.
memLen = 5;
degLen = 3;
modType = 'memPoly';
Load the in, out, fs, ovs, g0, and Tstep variables from the Preprocess Measured Data for PA Model Identification example.
load('step1.mat')
To compute the model coefficient matrix, use a predistorted waveform as it has a larger dynamic range. You later use the coefficient matrix to verify the quality of the fitted model.
fitCoefMat = helperPACharMemPolyModel('coefficientFinder', ... in(:,2),out(:,2),memLen,degLen,modType);
Alternatively, you can use a subset of the data range to fit the model
fitCoefMat = helperPACharMemPolyModel('coefficientFinder', ... in(14e4:15e4,2), out(14e4:15e4,2),memLen,degLen,modType);
Verify the quality of the PA model by computing the RMS error of the fitting, as well as by plotting the fitted and measured waveforms in the time domain, the power transfer function, the spectrum, and the ACLR spectral measurement.
First, verify the quality of the fitted model by comparing the measurement and the prediction using the original data.
helperPAVerifyMemPolyModel(in(:,1),out(:,1),fitCoefMat,modType,fs*ovs);
Signal standard deviation = 7.8385% ACPR data = -36.9763 -37.6772 ACPR fit = -37.4842 -38.3254

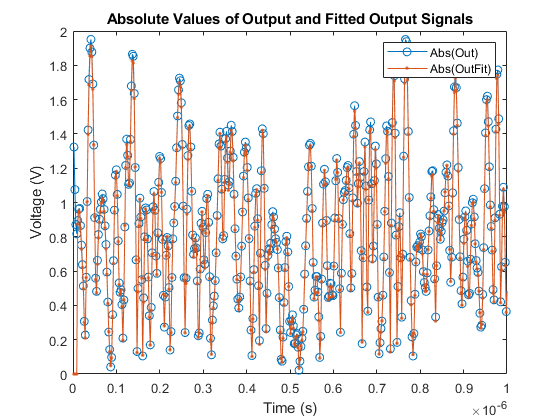

Then, verify the quality of the model using the measured data with the iterative direct digital predistortion (DPD) approach. This data has also been used to identify the PA model.
helperPAVerifyMemPolyModel(in(:,2),out(:,2),fitCoefMat,modType,fs*ovs);
Signal standard deviation = 3.3434% ACPR data = -38.0929 -38.5962 ACPR fit = -38.5555 -38.8375
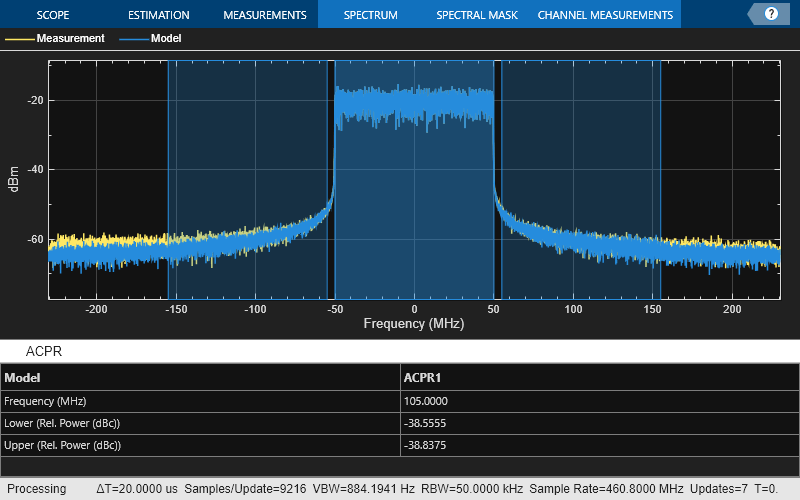

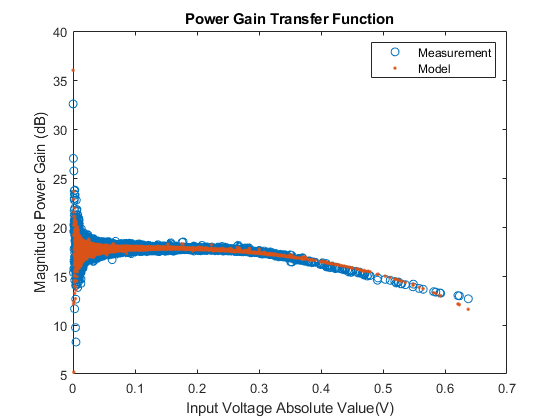
Finally, save the PA model and relevant parameters for later use.
close all; save('PA_model', 'Tstep','degLen','memLen','modType','fitCoefMat', 'g0');
Use Grid Search Function to Assess Best Order and Memory Depth
Verify the order and memory depth of the PA model that minimize the time domain RMS error. Use a grid search algorithm that you can parallelize on multicore machines.
rmsErrorFreq = helperPACharGridSearchTime(in(:,2),out(:,2),modType,7);
Starting parallel pool (parpool) using the 'Processes' profile ... 06-Aug-2024 18:16:37: Job Queued. Waiting for parallel pool job with ID 1 to start ... 06-Aug-2024 18:17:37: Job Queued. Waiting for parallel pool job with ID 1 to start ... Connected to parallel pool with 4 workers.
