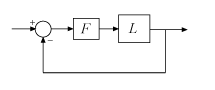
wcdiskmargin
Worst-case disk-based stability margins of uncertain feedback loops
Syntax
Description
The worst-case disk margin is the smallest disk margin that occurs within a
specified uncertainty range. It is also the minimum guaranteed margin over the uncertainty
range. wcdiskmargin estimates the worst-case disk margins and
corresponding worst-case gain and phase margins for both loop-at-a-time and multiloop
variations. The function also returns the worst-case perturbation, the combination of
uncertain elements that yields the weakest margins.
[
estimates the worst-case loop-at-a-time disk-based stability margins for the uncertain
negative feedback loop wcDM,wcu] = wcdiskmargin(L,'siso')feedback(L,eye(N)), where N is
the number of inputs and outputs in L.
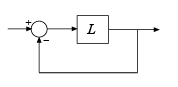
While diskmargin
computes stability margins for a nominal model, wcdiskmargin computes
the worst-case (smallest) disk margin over the modeled uncertainty in
L. Disk-based margin analysis provides a stronger guarantee of robust
stability than the classical gain and phase margins. For general information about disk
margins, see Stability Analysis Using Disk Margins.
___ = wcdiskmargin(___,
specifies an additional skew parameter that biases the modeled gain and phase variation
toward gain increase (positive sigma)sigma) or gain decrease (negative
sigma). You can use this argument to test the relative sensitivity of
stability margins to gain increases versus decreases. You can use this argument with any of
the previous syntaxes.
[___,
returns a structure with additional information about the worst-case margins and the
perturbations that generate them. You can use this output argument with any of the previous
syntaxes.info] = wcdiskmargin(___)
Examples
Use wcdiskmargin to compute worst-case loop-at-a-time and multiloop disk margins. This example illustrates that loop-at-a-time margins can give an overly optimistic assessment of the true robustness of MIMO feedback loops. Margins of individual loops can be sensitive to small perturbations within other loops.
Consider the closed-loop system of the following illustration.
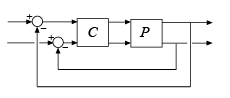
P is a two-input, two-output second-order plant and C is a 2x2 static gain. Construct P in state-space form, assuming that it has an uncertain parameter and some dynamic uncertainty. Compute the worst-case disk margins at the plant output (to compute the margins at the plant input, use L = C*Pu).
p = ureal('p',10,'Percentage',10); a = [-0.2 p;-p -0.2]; b = eye(2); c = [1 p;-p 1]; d = zeros(2,2); P = ss(a,b,c,0); DEL = ultidyn('DEL',[2 2],'Bound',0.1); Pu = P*(eye(2)+DEL); C = [1 -2;0 1]; L = Pu*C; [wcDM,wcu] = wcdiskmargin(L,'siso');
Examine the worst-case loop-at-a-time disk margins, returned in the structure array wcDM. Each entry in this structure array contains the worst-case stability margins of the corresponding channel.
wcDM(1)
ans = struct with fields:
GainMargin: [0.5298 1.8875]
PhaseMargin: [-34.1696 34.1696]
DiskMargin: 0.6147
LowerBound: 0.6147
UpperBound: 0.6160
CriticalFrequency: 0
WorstPerturbation: [2×2 ss]
The result in wcDM(1) gives guaranteed stability margins for the specified uncertainty range. As long as the open-loop gain of the first channel changes by a factor between 0.53 and 1.88, the closed loop remains stable for all (p,DEL) values within the specified range. Similarly, the closed loop remains stable as long as the phase variation does not exceed 34° in absolute value.
Similarly, wcDM(2) shows that in the second feedback channel, the gain can vary by any factor between 0.52 and 1.93 or the phase can vary by up to 35°, and the system remains stable for such variations and the (p,DEL) uncertainty.
wcDM(2)
ans = struct with fields:
GainMargin: [0.5167 1.9352]
PhaseMargin: [-35.3450 35.3450]
DiskMargin: 0.6372
LowerBound: 0.6372
UpperBound: 0.6386
CriticalFrequency: -2.2950e-08
WorstPerturbation: [2×2 ss]
The lower bound returned by wcdiskmargin is a theoretical minimum guaranteed worst-case disk margin. The upper bound corresponds to an actual perturbation in the specified uncertainty range that approaches the lower-bound prediction. The output wcu contains the values of that perturbation for each feedback channel. For example, wcu(2) is the worst combination of (alpha,DEL) for the second channel, and the disk margins for this worst combination are close to wcDM(2). In particular, DM(2).UpperBound and wcDM(1).UpperBound match.
wcL = usubs(L,wcu(2)); DM = diskmargin(wcL); DM(2)
ans = struct with fields:
GainMargin: [0.5159 1.9382]
PhaseMargin: [-35.4184 35.4184]
DiskMargin: 0.6386
LowerBound: 0.6386
UpperBound: 0.6386
Frequency: 2.2950e-08
WorstPerturbation: [2×2 ss]
In practice, gain and phase variations affect both channels simultaneously. To estimate the stability margins with respect to such independent and concurrent variations, examine the worst-case multiloop disk margins.
wcMM = wcdiskmargin(L,'mimo')wcMM = struct with fields:
GainMargin: [0.8836 1.1317]
PhaseMargin: [-7.0729 7.0729]
DiskMargin: 0.1236
LowerBound: 0.1236
UpperBound: 0.1239
CriticalFrequency: 0
WorstPerturbation: [2×2 ss]
The multiloop margins are much weaker than when considering one loop at a time. This is because it takes a smaller amount of gain (or phase) variation to destabilize the feedback loop when both channels are subject to variations.
You can visualize how uncertainty affects the margins with wcdiskmarginplot. This plots the (disk-based) gain and phase margins as a function of frequency for the nominal and worst-case values of (alpha,DEL) as well as 20 random samples of this uncertainty. The plot shows that uncertainty weakens the margins most near DC.
wcdiskmarginplot(L,{1e-1,1e1})
legend('location','NorthWest')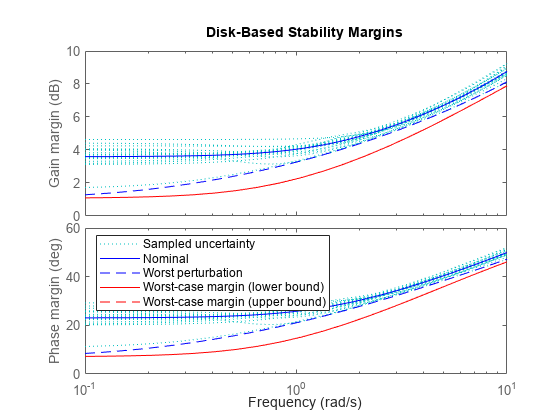
Finally, compute the multiloop margin for simultaneous variations in gain (or phase) at both the plant inputs and plant outputs. When you allow the gain (or phase) to vary in more places, it becomes easier to destabilize the feedback loop, so the margins get even smaller. Thus, the multiloop I/O margin provides the most comprehensive and most conservative assessment of robust stability in the face of gain or phase variations and (alpha,DEL) uncertainty.
wcMMIO = wcdiskmargin(Pu,C)
wcMMIO = struct with fields:
GainMargin: [0.9363 1.0680]
PhaseMargin: [-3.7681 3.7681]
DiskMargin: 0.0658
LowerBound: 0.0658
UpperBound: 0.0659
CriticalFrequency: 1.0000e-04
WorstPerturbation: [1×1 struct]
Input Arguments
Uncertain open-loop response, specified as an uncertain model such as a
uss or ufrd model. L
can be SISO or MIMO, as long as it has the same number of inputs and outputs.
wcdiskmargin computes the worst-case disk-based stability margins
for the negative-feedback closed-loop system
feedback(L,eye(N)).

To compute the worst-case disk margins of the positive feedback system
feedback(L,eye(N),+1), use
wcdiskmargin(-L).
When you have a controller P and a plant C,
you can compute the worst-case disk margins for gain (or phase) variations at the plant
inputs or outputs, as in the following diagram.
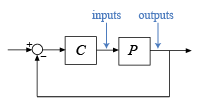
To compute margins at the plant outputs, set
L = P*C.To compute margins at the plant inputs, set
L = C*P.To consider variations at both the plant inputs and the plant output, use the syntax
[wcMMIO,wcu] = wcdiskmargin(P,C)instead.
L can be continuous time or discrete time. If
L is a generalized state-space model (genss)
then wcdiskmargin uses the current value of the tunable control
design blocks in L.
If L is a frequency-response data model (such as
ufrd), then wcdiskmargin computes the
margins at each frequency represented in the model. The function returns the worst-case
margins at the frequency with the smallest disk margin.
If L is a model array, then wcdiskmargin
computes margins for each model in the array.
Plant, specified as an uncertain model such as a uss or
ufrd model. P can be SISO or MIMO, as long
as P*C has the same number of inputs and outputs.
wcdiskmargin computes the worst-case disk margins for a
negative-feedback closed-loop system. To compute the disk margins of the system with
positive feedback, use wcdiskmargin(P,-C).
P can be continuous time or discrete time. If
P is a generalized state-space model (genss)
then wcdiskmargin uses the current value of the tunable control
design blocks in P.
If P is a frequency-response data model (such as
frd), then wcdiskmargin computes the margins
at each frequency represented in the model. The function returns the worst-case margins
at the frequency with the smallest disk margin.
Controller, specified as a dynamic system model. C can be SISO
or MIMO, as long as P*C has the same number of inputs and outputs.
wcdiskmargin computes the disk-based stability margins for a
negative-feedback closed-loop system. To compute the disk margins of the system with
positive feedback, use wcdiskmargin(-C,P).
C can be continuous time or discrete time. If
C is a generalized state-space model (genss)
then wcdiskmargin uses the current value of the tunable control
design blocks in C.
If C is a frequency-response data model (such as
frd), then wcdiskmargin computes the margins
at each frequency represented in the model. The function returns the worst-case margins
at the frequency with the smallest disk margin.
Skew of uncertainty region used to compute the stability margins, specified as a real scalar value. This parameter biases the uncertainty used to model gain and phase variations toward gain increase or gain decrease.
The default
sigma= 0 uses a balanced model of gain variation in a range[gmin,gmax], withgmin = 1/gmax.Positive
sigmauses a model with more gain increase than decrease (gmin > 1/gmax).Negative
sigmauses a model with more gain decrease than increase (gmin < 1/gmax).
Use the default sigma = 0 to get unbiased estimates of gain and
phase margins. You can test relative sensitivity to gain increase and decrease by
comparing the margins obtained with both positive and negative
sigma values. For more detailed information about how the choice
of sigma affects the margin computation, see Stability Analysis Using Disk Margins.
Options for worst-case computation, specified as an object you create with
wcOptions. The available options include settings that let
you:
Extract frequency-dependent worst-case margins.
Examine the sensitivity of the worst-case margins to each uncertain element.
Improve the results of the worst-case margin calculation by setting certain options for the underlying
mussvcalculation.
For more information about all available options, see wcOptions.
Example: wcOptions('Sensitivity','on','MussvOptions','m3')
Output Arguments
Worst-case disk margins for each feedback channel with all other loops closed,
returned as a structure for SISO feedback loops, or an N-by-1
structure array for a MIMO loop with N feedback channels. The fields
of wcDM(i) are:
| Field | Value |
|---|---|
GainMargin | Minimum guaranteed disk-based gain margin of the corresponding feedback
channel, returned as a vector of the form [gmin,gmax]. These
values mean that as long as the open-loop gain of the ith
channel changes by a factor no less than gmin and no more
than gmax, the closed loop remains stable for all uncertainty
values within the ranges specified in L. If the open-loop
gain can change sign without loss of stability, gmin can be
less than zero for large enough negative sigma. If the
closed-loop system goes unstable for some combination of uncertainty values,
then wcDM(i).GainMargin = [1 1]. |
PhaseMargin | Minimum guaranteed disk-based phase margin of the corresponding feedback
channel, returned as a vector of the form [-pm,pm] in
degrees. If the closed-loop system goes unstable for some combination of
uncertainty values, then wcDM(i).PhaseMargin = [0 0]. |
DiskMargin | Minimum guaranteed disk margin (see Stability Analysis Using Disk Margins for the
definition and interpretation of the disk margin). If the closed-loop system is
unstable for some combination of uncertain-element values, then
wcDM(i).DiskMargin = 0. |
LowerBound | Lower bound on worst-case disk margin. This value is the same as
DiskMargin. |
UpperBound | Upper bound on worst-case disk margin. This value is the disk margin
obtained for the worst perturbation found by wcdiskmargin,
returned as wcu(i). The actual
worst-case disk margin is no better than this value. |
CriticalFrequency | Frequency at which the disk margin for the worst perturbation
wcu(i) is weakest, as a function of frequency. This value
is in rad/TimeUnit, where TimeUnit is the
TimeUnit property of L. |
WorstPerturbation | Smallest gain and phase variation that drives the feedback loop
unstable for the worst-case combination of uncertain elements. The
perturbation is returned as a state-space (
This state-space model is a diagonal perturbation of the
form For more information on interpreting
This field is different from the
|
When L = P*C is the open-loop response of a system comprising a
controller and plant with unit negative feedback in each channel,
wcDM contains the stability margins for variations at the plant
outputs. To compute the stability margins for variations at the plant inputs, use
L = C*P. To compute the stability margins for simultaneous,
independent variations at both the plant inputs and outputs, use wcMMIO =
wcdiskmargin(P,C).
When L is a model array, wcDM has
additional dimensions corresponding to the array dimensions of L.
For instance, if L is a 1-by-3 array of two-input, two-output
models, then wcDM is a 2-by-3 structure array.
wcDM(j,k) contains the margins for the
jth feedback channel of the kth
model in the array.
Perturbation of uncertain elements yielding the weakest margins, returned as:
A structure array of dimensions N-by-1 for loop-at-a-time margins, where N is the number of feedback channels
A scalar structure for multiloop margins
The lower bound returned by wcdiskmargin is a theoretical
minimum guaranteed worst-case disk margin. The upper bound corresponds to an actual
perturbation in the specified uncertainty range that approaches the lower-bound
prediction. wcu contains the values of that perturbation. For
example, if the input system includes uncertain elements M and
delta, then wcu.M and
wcu.delta contain the worst perturbations found by
wcdiskmargin. It is possible that a worse perturbation exists,
but no perturbation can yield a worse margin than the lower bound returned by
wcdiskmargin.
Use usubs to substitute these values for the uncertain elements
in the input system, to obtain the dynamic system that has the worst-case disk
margin.
Worst-case multiloop disk margins, returned as a structure. The gain (or phase)
margins quantify how much gain variation (or phase variation) the system can tolerate in
all feedback channels at once while remaining stable. Thus, wcMM is
a single structure regardless of the number of feedback channels in the system. (For
SISO systems, wcMM = wcDM.) The fields of
wcMM are:
| Field | Value |
|---|---|
GainMargin | Minimum guaranteed multiloop disk-based gain margin, returned as a vector
of the form [gmin,gmax]. These values mean that as long as
the gain in all loop channels changes by a factor no less than
gmin and no more than gmax, the closed
loop remains stable for all uncertainty values within the ranges specified in
L. If the closed-loop system goes unstable for some
combination of uncertainty values, then wcMM.GainMargin = [1
1]. |
PhaseMargin | Minimum guaranteed multiloop disk-based phase margin, returned as a vector
of the form [-pm,pm] in degrees. If the closed-loop system
goes unstable for some combination of uncertainty values, then
wcMM.PhaseMargin = [0 0]. |
DiskMargin | Minimum guaranteed disk margin (see Stability Analysis Using Disk Margins for the
definition and interpretation of the disk margin). If the closed-loop system is
unstable for some combination of uncertain-element values, then
wcMM.DiskMargin = 0. |
LowerBound | Lower bound on worst-case disk margin. This value is the same as
DiskMargin. |
UpperBound | Upper bound on worst-case disk margin. This value is the disk margin
obtained for the worst perturbation found by wcdiskmargin,
returned as wcu. The actual worst-case multiloop disk
margin is no better than this value. |
CriticalFrequency | Frequency at which the disk margin for the worst perturbation
wcu is weakest, as a function of frequency. This value is
in rad/TimeUnit, where TimeUnit is the
TimeUnit property of L. |
WorstPerturbation | Smallest gain and phase variation that drives the feedback loop
unstable for the worst-case combination of uncertain elements. The
perturbation is returned as a state-space (
This state-space model is a diagonal perturbation of the
form For more information on interpreting
This field is different from the
|
When L = P*C is the open-loop response of a system comprising a
controller and plant with unit negative feedback in each channel,
wcMM contains the stability margins for variations at the plant
outputs. To compute the stability margins for variations at the plant inputs, use
L = C*P. To compute the stability margins for simultaneous,
independent variations at both the plant inputs and outputs, use wcMMIO =
wcdiskmargin(P,C).
When L is a model array, wcMM is a
structure array with one entry for each model in L.
Worst-case disk margins for independent variations in all input and output channels
of the plant P, returned as a structure having the same fields as
wcMM.
For variations applied simultaneously at inputs and outputs, the
WorstPerturbation field is itself a structure with fields
Input and Output. Each of these fields contains
a state-space model such that for Fi(s) =
wcMMIO.WorstPerturbation.Input and Fo(s) =
wcMMIO.WorstPerturbation.Output, the system of the following diagram is
marginally unstable, with a pole on the stability boundary at the frequency
wcMMIO.CriticalFrequency, when P is evaluated
with the worst-case uncertainty values wcu.
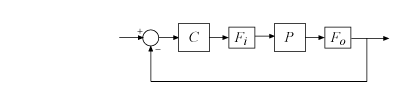
These state-space models Input and Output are
diagonal perturbations of the form F(s) = diag(f1(s),...,fN(s)). Each
fj(s) is a real-parameter dynamic system that realizes the
worst-case complex gain and phase variation applied to each channel of the feedback
loop.
Additional information about the worst-case values, returned as a structure with the following fields:
| Field | Description |
|---|---|
| Index of the model that has the smallest disk margin, when
|
| Frequency points at which
The |
| Lower and upper bounds on the actual worst-case disk margin of the
model, returned as an array. |
| Worst perturbations at each frequency point in
|
| Sensitivity of the worst-case disk margin to each uncertain element,
returned as a structure when the If the
|
Tips
wcdiskmarginassumes negative feedback. To compute the worst-case disk margins of a positive feedback system, usewcdiskmargin(-L)orwcdiskmargin(P,-C).You can visualize worst-case disk margins with
wcdiskmarginplot.
Algorithms
wcdiskmargin models gain (and phase) variation as
umargin uncertainty, combines it with the specified plant uncertainty,
and uses mussv to compute the worst-case disk margins and perturbation.
This generalizes the diskmargin algorithm to feedback loops with
uncertainty. For more information about disk-margin computation and interpretation, see Stability Analysis Using Disk Margins.
Version History
Introduced in R2018bThe wcdiskmargin command returns disk-based gain margins in the
GainMargin field of its output structures wcDM,
wcMM, and wcMMIO. These margins take the form
[gmin,gmax], meaning that the open-loop gain can be multiplied by any
factor in that range without loss of closed-loop stability. Beginning in R2020a, the lower
end of the range gmin can be negative for some negative values of the
skew sigma, if the closed-loop system remains stable even if the sign
of the open-loop gain changes. The skew controls the bias in the disk-based gain margin
toward gain decrease or increase (see Stability Analysis Using Disk Margins). Previously, the
gain-margin range was always positive.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)