Load Predefined Control System Environments
Reinforcement Learning Toolbox™ software provides several predefined environments representing dynamical systems that are often used as benchmarks cases for control systems design.
In these environments, the state and observation (which are predefined) belong to nonfinite numerical vector spaces, while the action (also predefined) can still belong to a finite set. The (deterministic) state transitions laws are derived by discretizing the dynamics of an underlying physical system.
Environments that rely on an underlying Simulink® model for the calculation of the state transition, reward and observation, are referred to as Simulink environments. Some of the predefined control system environments belong to this category.
Multiagent environments are environments in which you can train and simulate multiple agents together. Some of the predefined MATLAB® and Simulink control system environments are multiagent environments.
You can use predefined control system environments to learn how to apply reinforcement learning to the control of physical systems, gain familiarity with Reinforcement Learning Toolbox software features, or test your own agents.
To load the following predefined MATLAB control system environments, use the rlPredefinedEnv
function. Each of these predefined environment is available in two versions, one with a
discrete action space, the other with a continuous action space.
| Environment | Agent Task |
|---|---|
| Double integrator | Control a second-order dynamic system using either a discrete or continuous action space. |
| Cart-pole | Balance a pole on a moving cart by applying forces to the cart using either a discrete or continuous action space. |
| Simple pendulum with image observation | Swing up and balance a simple pendulum using either a discrete or continuous action space. |
You can also load the following predefined Simulink environments using the rlPredefinedEnv
function. For these environments, rlPredefinedEnv creates a SimulinkEnvWithAgent
object. Each of these predefined environment is also available in two versions, one with a
discrete action space, the other with a continuous action space.
| Environment | Agent Task |
|---|---|
| Simple pendulum Simulink model | Swing up and balance a simple pendulum using either a discrete or continuous action space. |
| Cart-pole Simscape™ model | Balance a pole on a moving cart by applying forces to the cart using either a discrete or continuous action space. |
You can also load predefined grid world environments. For more information, see Load Predefined Grid World Environments.
To learn how to create your own custom environment, see Create Custom Environment Using Step and Reset Functions, Create Custom Simulink Environments and Create Custom Environment from Class Template.
Double Integrator Environments
The goal of the agent in the predefined double integrator environments is to control the position of a mass in a frictionless mono-dimensional space by applying a force input. The system has a second-order dynamics that can be represented by a double integrator (that is two integrators in series).
In this environment, a training episode ends when either of the following events occurs:
The mass moves beyond a given threshold from the origin.
The norm of the state vector is less than a given threshold.
There are two double integrator environment variants, which differ by the agent action space.
Discrete — Agent can apply a force of either Fmax or -Fmax to the cart, where Fmax is the
MaxForceproperty of the environment.Continuous — Agent can apply any force within the range [-Fmax,Fmax].
To create a double integrator environment, use the rlPredefinedEnv
function.
Discrete action space
env = rlPredefinedEnv('DoubleIntegrator-Discrete');Continuous action space
env = rlPredefinedEnv('DoubleIntegrator-Continuous');
You can visualize the double integrator environment using the plot
function. The plot displays the mass as a red rectangle.
plot(env)
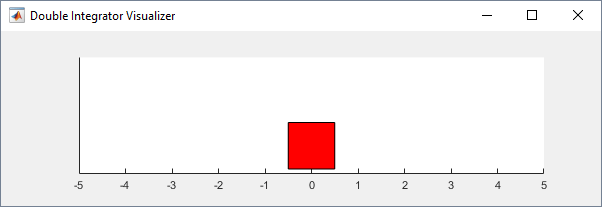
To visualize the environment during training, call plot before
training and keep the visualization figure open.
For examples showing how to train agents in double integrator environments, see the following:
Environment Properties
| Property | Description | Default |
|---|---|---|
Gain | Gain for the double integrator | 1 |
Ts | Sample time in seconds | 0.1 |
MaxDistance | Distance magnitude threshold in meters | 5 |
GoalThreshold | State norm threshold | 0.01 |
Q | Weight matrix for observation component of reward signal | [10 0; 0 1] |
R | Weight matrix for action component of reward signal | 0.01 |
MaxForce | Maximum input force in newtons | Discrete: Continuous:
|
State | Environment state, specified as a column vector with the following state variables:
| [0 0]' |
Actions
In the double integrator environments, the agent interacts with the environment using a single action signal, the force applied to the mass. The environment contains a specification object for this action signal. For the environment with a:
Discrete action space, the specification is an
rlFiniteSetSpecobject.Continuous action space, the specification is an
rlNumericSpecobject.
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the double integrator system, the agent can observe both of the environment state
variables in env.State. For each state variable, the environment
contains an rlNumericSpec
observation specification. Both states are continuous and unbounded.
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment is the discrete-time equivalent of the following continuous-time reward, which is analogous to the cost function of an LQR controller.
Here:
QandRare environment properties.x is the environment state vector.
u is the input force.
Cart-Pole Environments
The goal of the agent in the predefined cart-pole environments is to balance a pole on a moving cart by applying horizontal forces to the cart. The pole is considered successfully balanced if both of the following conditions are satisfied:
The pole angle remains within a given threshold of the vertical position, where the vertical position is zero radians.
The magnitude of the cart position remains below a given threshold.
There are two cart-pole environment variants, which differ by the agent action space.
Discrete — Agent can apply a force of either Fmax or -Fmax to the cart, where Fmax is the
MaxForceproperty of the environment.Continuous — Agent can apply any force within the range [-Fmax,Fmax].
To create a cart-pole environment, use the rlPredefinedEnv
function.
Discrete action space
env = rlPredefinedEnv('CartPole-Discrete');Continuous action space
env = rlPredefinedEnv('CartPole-Continuous');
You can visualize the cart-pole environment using the plot
function. The plot displays the cart as a blue square and the pole as a red
rectangle.
plot(env)
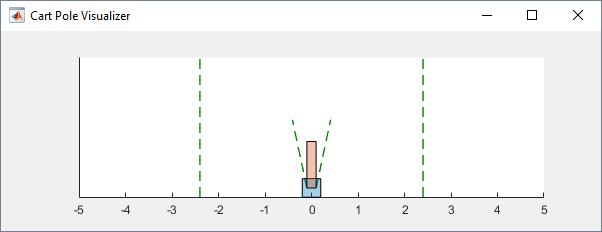
To visualize the environment during training, call plot before
training and keep the visualization figure open.
For examples showing how to train agents in cart-pole environments, see the following:
Environment Properties
| Property | Description | Default |
|---|---|---|
Gravity | Acceleration due to gravity in meters per second squared | 9.8 |
MassCart | Mass of the cart in kilograms | 1 |
MassPole | Mass of the pole in kilograms | 0.1 |
Length | Half the length of the pole in meters | 0.5 |
MaxForce | Maximum horizontal force magnitude in newtons | 10 |
Ts | Sample time in seconds | 0.02 |
ThetaThresholdRadians | Pole angle threshold in radians | 0.2094 |
XThreshold | Cart position threshold in meters | 2.4 |
RewardForNotFalling | Reward for each time step the pole is balanced | 1 |
PenaltyForFalling | Reward penalty for failing to balance the pole | Discrete — Continuous —
|
State | Environment state, specified as a column vector with the following state variables:
| [0 0 0 0]' |
Actions
In the cart-pole environments, the agent interacts with the environment using a single scalar action signal, the horizontal force applied to the cart. The environment contains a specification object for this action signal. For the environment with a:
Discrete action space, the specification is an
rlFiniteSetSpecobject.Continuous action space, the specification is an
rlNumericSpecobject.
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the cart-pole system, the agent can observe all the environment state variables in
env.State. For
each state variable, the environment contains an rlNumericSpec
observation specification. All the states are continuous and unbounded.
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment consists of two components.
A positive reward for each time step that the pole is balanced, that is, the cart and pole both remain within their specified threshold ranges. This reward accumulates over the entire training episode. To control the size of this reward, use the
RewardForNotFallingproperty of the environment.A one-time negative penalty if either the pole or cart moves outside of their threshold range. At this point, the training episode stops. To control the size of this penalty, use the
PenaltyForFallingproperty of the environment.
Simple Pendulum Environments with Image Observation
This environment is a simple frictionless pendulum that is initially hangs in a downward position. The training goal is to make the pendulum stand upright without falling over using minimal control effort.
There are two simple pendulum environment variants, which differ by the agent action space.
Discrete — Agent can apply a torque of
-2,-1,0,1, or2to the pendulum.Continuous — Agent can apply any torque within the range [
-2,2].
To create a simple pendulum environment, use the
rlPredefinedEnv
function.
Discrete action space
env = rlPredefinedEnv('SimplePendulumWithImage-Discrete');Continuous action space
env = rlPredefinedEnv('SimplePendulumWithImage-Continuous');
For examples showing how to train an agent in this environment, see the following:
Environment Properties
| Property | Description | Default |
|---|---|---|
Mass | Pendulum mass | 1 |
RodLength | Pendulum length | 1 |
RodInertia | Pendulum moment of inertia | 0 |
Gravity | Acceleration due to gravity in meters per second squared | 9.81 |
DampingRatio | Damping on pendulum motion | 0 |
MaximumTorque | Maximum input torque in newtons | 2 |
Ts | Sample time in seconds | 0.05 |
State | Environment state, specified as a column vector with the following state variables:
| [0 0 ]' |
Q | Weight matrix for observation component of reward signal | [1 0;0 0.1] |
R | Weight matrix for action component of reward signal | 1e-3 |
Actions
In the simple pendulum environments, the agent interacts with the environment using a single action signal, the torque applied at the base of the pendulum. The environment contains a specification object for this action signal. For the environment with a:
Discrete action space, the specification is an
rlFiniteSetSpecobject.Continuous action space, the specification is an
rlNumericSpecobject.
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the simple pendulum environment, the agent receives the following observation signals:
50-by-50 grayscale image of the pendulum position
Derivative of the pendulum angle
For each observation signal, the environment contains an rlNumericSpec
observation specification. All the observations are continuous and unbounded.
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment is
Here:
θt is the pendulum angle of displacement from the upright position.
is the derivative of the pendulum angle.
ut-1 is the control effort from the previous time step.
Simple Pendulum Simulink Model
This environment is a simple frictionless pendulum that initially hangs in a downward
position. The training goal is to make the pendulum stand upright without falling over using
minimal control effort. The model for this environment is defined in the
rlSimplePendulumModel
Simulink model.
open_system('rlSimplePendulumModel')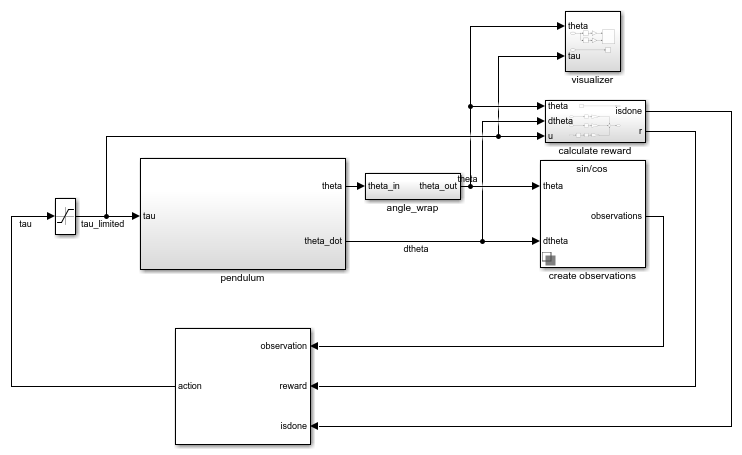
There are two simple pendulum environment variants, which differ by the agent action space.
Discrete — Agent can apply a torque of either Tmax,
0, or -Tmax to the pendulum, where Tmax is themax_tauvariable in the model workspace.Continuous — Agent can apply any torque within the range [-Tmax,Tmax].
To create a simple pendulum environment, use the rlPredefinedEnv
function.
Discrete action space
env = rlPredefinedEnv('SimplePendulumModel-Discrete');Continuous action space
env = rlPredefinedEnv('SimplePendulumModel-Continuous');
For examples that train agents in the simple pendulum environment, see:
Actions
In the simple pendulum environments, the agent interacts with the environment using a single action signal, the torque applied at the base of the pendulum. The environment contains a specification object for this action signal. For the environment with a:
Discrete action space, the specification is an
rlFiniteSetSpecobject.Continuous action space, the specification is an
rlNumericSpecobject.
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the simple pendulum environment, the agent receives the following three observation signals, which are constructed within the create observations subsystem.
Sine of the pendulum angle
Cosine of the pendulum angle
Derivative of the pendulum angle
For each observation signal, the environment contains an rlNumericSpec
observation specification. All the observations are continuous and unbounded.
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment, which is constructed in the calculate reward subsystem, is
Here:
θt is the pendulum angle of displacement from the upright position.
is the derivative of the pendulum angle.
ut-1 is the control effort from the previous time step.
Cart-Pole Simscape Model
The goal of the agent in the predefined cart-pole environments is to balance a pole on a moving cart by applying horizontal forces to the cart. The pole is considered successfully balanced if both of the following conditions are satisfied:
The pole angle remains within a given threshold of the vertical position, where the vertical position is zero radians.
The magnitude of the cart position remains below a given threshold.
The model for this environment is defined in the
rlCartPoleSimscapeModel
Simulink model. The dynamics of this model are defined using Simscape
Multibody™.
open_system('rlCartPoleSimscapeModel')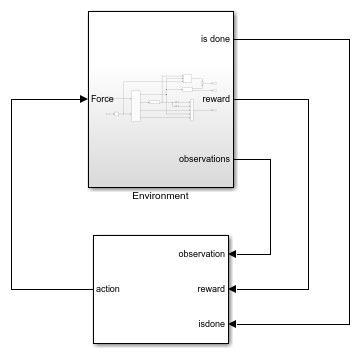
In the Environment subsystem, the model dynamics are defined using Simscape components and the reward and observation are constructed using Simulink blocks.
open_system('rlCartPoleSimscapeModel/Environment')
There are two cart-pole environment variants, which differ by the agent action space.
Discrete — Agent can apply a force of
15,0, or-15to the cart.Continuous — Agent can apply any force within the range [
-15,15].
To create a cart-pole environment, use the rlPredefinedEnv
function.
Discrete action space
env = rlPredefinedEnv('CartPoleSimscapeModel-Discrete');Continuous action space
env = rlPredefinedEnv('CartPoleSimscapeModel-Continuous');
For an example that trains an agent in this cart-pole environment, see Train DDPG Agent to Swing Up and Balance Cart-Pole System.
Actions
In the cart-pole environments, the agent interacts with the environment using a single action signal, the force applied to the cart. The environment contains a specification object for this action signal. For the environment with a:
Discrete action space, the specification is an
rlFiniteSetSpecobject.Continuous action space, the specification is an
rlNumericSpecobject.
For more information on obtaining action specifications from an environment, see
getActionInfo.
Observations
In the cart-pole environment, the agent receives the following five observation signals.
Sine of the pole angle
Cosine of the pole angle
Derivative of the pendulum angle
Cart position
Derivative of cart position
For each observation signal, the environment contains an rlNumericSpec
observation specification. All the observations are continuous and unbounded.
For more information on obtaining observation specifications from an environment, see
getObservationInfo.
Reward
The reward signal for this environment is the sum of two components (r = rqr + rn + rp):
A quadratic regulator control reward, constructed in the
Environment/qr rewardsubsystem.A cart limit penalty, constructed in the
Environment/x limit penaltysubsystem. This subsystem generates a negative reward when the magnitude of the cart position exceeds a given threshold.
Here:
x is the cart position.
θ is the pole angle of displacement from the upright position.
ut-1 is the control effort from the previous time step.
See Also
Functions
rlPredefinedEnv|train|sim|reset
