meanDifferenceModel
Identify most degraded cell in serially connected lithium-ion battery pack
Since R2022b
Syntax
Description
meanDifferenceModel( analyzes the
consistency of the open-circuit voltage (OCV) for each cell in a serially connected
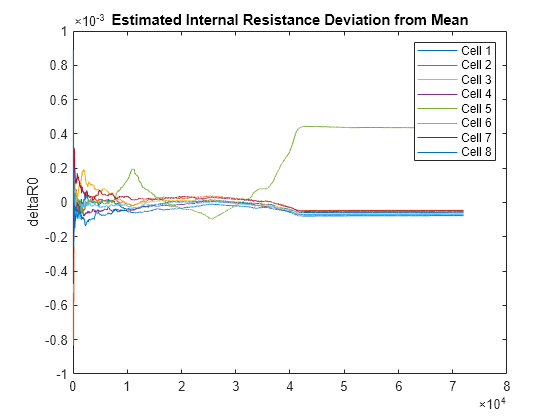
lithium-ion battery pack and plots the results. The software combines the recursive least
square (RLS) algorithm with the mean-difference model (MDM) to estimate the deviation of the
OCV of each cell from the mean OCV of the pack [1]. The larger the
deviation is in the negative direction, the more likely it is that the battery pack has a
fault condition, such as an internal short circuit. The plot legend identifies the cell with
the highest deviation, and therefore, the worst cell in the
pack.data)
The algorithm imposes no restrictions on battery activity during the collection of
data. The battery can be in any operating sequence, including
charging, discharging, and standby phases.
meanDifferenceModel(
incorporates additional options specified by one or more name-value arguments. For example,
set the data,Name=Value)CurrentVariable argument to 10 to specify that
the column with index 10 contains the pack current values.
[
returns the index of the worst cell worstcell,deltae,deltar0] = meanDifferenceModel(___)worstcell, the deviation
deltae of the cell voltages from the mean OCV, and the deviation
deltar0 of the internal resistances from the mean
R0 value. You can use this syntax with any of
the previous input-argument combinations.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Ouyang, Minggao, Mingxuan Zhang, Xuning Feng, Languang Lu, Jianqiu Li, Xiangming He, and Yuejiu Zheng. “Internal Short Circuit Detection for Battery Pack Using Equivalent Parameter and Consistency Method.” Journal of Power Sources 294 (October 2015): 272–83. https://doi.org/10.1016/j.jpowsour.2015.06.087.
Extended Capabilities
Version History
Introduced in R2022b