phased.FMCWWaveform
FMCW waveform
Description
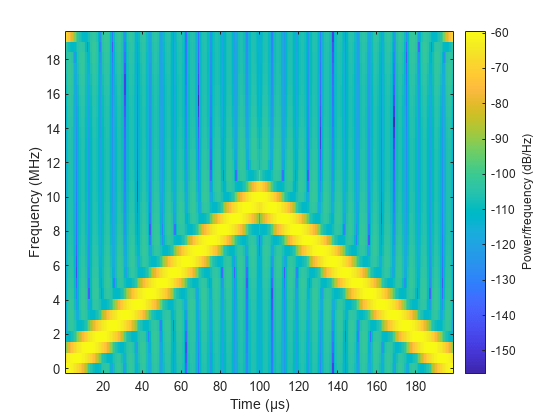
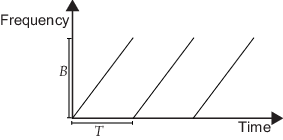
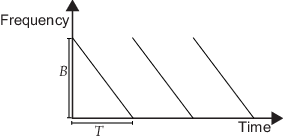
The phased.FMCWWaveform object creates an FMCW (frequency modulated continuous
wave) waveform.
To create and use the object:
Create the
phased.FMCWWaveformobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
waveform = phased.FMCWWaveformphased.FMCWWaveform
System object™, waveform, with default property values.
waveform = phased.FMCWWaveform(Name=Value)Name set to the specified
Value. You can specify additional name-value pair arguments in any
order as
(Name1=Value1,...,NameN=ValueN).
Properties
Usage
Syntax
Description
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Issakov, Vadim. Microwave Circuits for 24 GHz Automotive Radar in Silicon-based Technologies. Berlin: Springer, 2010.
[2] Skolnik, M.I. Introduction to Radar Systems. New York: McGraw-Hill, 1980.
Extended Capabilities
Version History
Introduced in R2012b
See Also
range2time | time2range | range2bw | phased.LinearFMWaveform
Topics
- Automotive Adaptive Cruise Control Using FMCW Technology (Radar Toolbox)