materialProperties
Material properties for structural, thermal, and electromagnetic analysis
Since R2023a
Description
A materialProperties object contains the description of
material properties for structural, thermal, and electromagnetic analysis. An femodel object contains
an array of materialProperties objects in its MaterialProperties property.
Creation
Syntax
Description
In R2025a: model.MaterialProperties = materialProperties(Material=
finds MaterialName)MaterialName in a built-in catalog and assigns all material
properties for this material from the catalog. This syntax sets all material properties as
properties of the
materialProperties object.
Note
The catalog specifies material properties in SI units.
model.MaterialProperties = materialProperties(Name=Value)
creates a material properties object and sets properties using one
or more name-value arguments. This syntax assigns the specified structural, thermal, or
electromagnetic material properties to the entire geometry of the
femodel object model.
Input Arguments
Cell or face IDs, specified as a vector of positive integers. Find the region IDs
using pdegplot with the
CellLabels (3-D) or FaceLabels (2-D) value set
to "on".
Data Types: double
Since R2025a
Material name from a catalog, specified as a string. When you specify a material from a catalog, the toolbox automatically assigns all material properties for this material in SI units. You can use any material name listed in this table, except for materials that are not supported in the toolbox:
"PEC"or"perfect-reflector"— Perfect electrical conductor"vegetation"— Vegetation
| Common Building Materials | Metals | Terrestrial Materials | Theoretical Materials |
|---|---|---|---|
|
|
|
|
Example: Material="teflon"
Data Types: string
Properties
Young's modulus of the material, specified as a positive number, three-element vector of positive numbers (for both 2-D and 3-D geometries), or function handle. Use a function handle to specify Young's modulus that depends on space. For details, see Nonconstant Parameters of Finite Element Model.
Specifying Young's modulus as a three-element vector of positive numbers (or a function handle returning a three-row matrix of positive numbers) means that the material is orthotropic. A matrix of positive numbers specifies the orthotropic Young's modulus along the Cartesian coordinates x, y, and z as [Ex Ey Ez]. For orthotropic materials, you must also specify a shear modulus and Poisson's ratio as three-row matrices of positive numbers or function handles returning three-row matrices of positive numbers.
Data Types: double
Poisson's ratio of the material, specified as a positive number, three-element
vector of positive numbers (for both 2-D and 3-D geometries), or function handle. Use a
function handle to specify Poisson's ratio that depends on space. For details, see Nonconstant Parameters of Finite Element Model. For isotropic
materials, the value must be in the range (0,0.5).
Specifying Poisson's ratio as a three-element vector of positive numbers (or a function handle returning a three-row matrix of positive numbers) means that the material is orthotropic. A matrix of positive numbers specifies the orthotropic Poisson's ratio along the Cartesian coordinates x, y, and z as [νxy νyz νxz]. For orthotropic materials, you must also specify Young's modulus and a shear modulus as three-element vectors of positive numbers or function handles returning three-row matrices of positive numbers.
Data Types: double
Shear modulus of the material, specified as a three-element vector of positive numbers (for both 2-D and 3-D geometries), or function handle. Specify shear modulus for orthotropic materials. Use a function handle to specify shear modulus that depends on space. For details, see Nonconstant Parameters of Finite Element Model.
Specifying a shear modulus indicates that the material is orthotropic. A matrix of positive numbers specifies the orthotropic shear modulus along the Cartesian coordinates x, y, and z as [Gxy Gyz Gxz]. For orthotropic materials, you must also specify Young's modulus and Poisson's ratio as three-element vectors of positive numbers or function handles returning three-row matrices of positive numbers.
Data Types: double
Mass density of the material, specified as a positive number or function handle. Use a function handle to specify mass density that depends on space. For details, see Nonconstant Parameters of Finite Element Model. This property is required when modeling gravitational effects.
Data Types: double
Coefficient of thermal expansion of the material, specified as a real number. This property is required for thermal stress analysis. Thermal stress analysis requires the structural model to be static.
Data Types: double
Thermal conductivity of the material, specified as a nonnegative number, matrix, or function handle. You can specify thermal conductivity for a steady-state or transient analysis. For orthotropic thermal conductivity, use a thermal conductivity matrix. Use a function handle to specify a thermal conductivity that depends on space, time, or temperature. For details, see Nonconstant Parameters of Finite Element Model.
Data Types: double | function_handle
Specific heat of the material, specified as a positive number or function handle. Specify this property for a transient thermal conduction analysis. Use a function handle to specify a specific heat that depends on space, time, or temperature. For details, see Nonconstant Parameters of Finite Element Model.
Data Types: double | function_handle
Hysteretic damping of the material, specified as a nonnegative number. This type of damping is also called structural damping.
Data Types: double
Relative permittivity of the material, specified as a number or function handle.
Use a positive number to specify a relative permittivity for an electrostatic analysis.
Use a real or complex number to specify a relative permittivity for a harmonic electromagnetic analysis.
Use a function handle to specify a relative permittivity that depends on the coordinates and, for a harmonic analysis, on the frequency. For details, see Nonconstant Parameters of Finite Element Model.
Data Types: double | function_handle
Complex Number Support: Yes
Relative permeability of the material, specified as a number or function handle. For a magnetostatic analysis:
Use a positive number to specify a constant relative permeability.
Use a function handle to specify a relative permeability that depends on the coordinates, magnetic potential and its gradients, and the norm of the magnetic flux density. For details, see Nonconstant Parameters of Finite Element Model.
For a harmonic analysis:
Use a real or complex number to specify a constant relative permeability.
Use a function handle to specify a relative permeability that depends on the coordinates and on the frequency. For details, see Nonconstant Parameters of Finite Element Model.
Data Types: double | function_handle
Complex Number Support: Yes
Conductivity of the material, specified as a nonnegative number or function handle. Use a function handle to specify a conductivity that depends on the coordinates and, for a harmonic analysis, on the frequency. For details, see Nonconstant Parameters of Finite Element Model.
Data Types: double | function_handle
Examples
Since R2025a
Specify materials for a bimetallic beam by their names.
First, create and plot a bimetallic beam geometry.
H = 0.1;
gm = multicuboid(0.5,0.1,[H,H],Zoffset=[0,H]);
pdegplot(gm,CellLabels="on",FaceAlpha=0.2);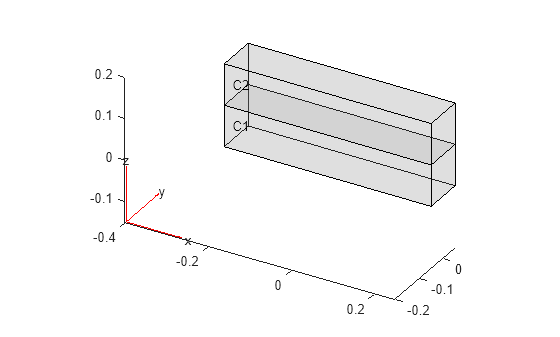
Create an femodel object for solving a transient structural problem, and assign the geometry to the model.
model = femodel(AnalysisType="structuralTransient", ... Geometry=gm);
Specify that cell 1 is a copper strip and cell 2 is an invar strip.
model.MaterialProperties(1) = materialProperties(Material="copper"); model.MaterialProperties(2) = materialProperties(Material="Invar")
model =
1×1 femodel array
Properties for analysis type: structuralTransient
AnalysisType: "structuralTransient"
Geometry: [1×1 fegeometry]
MaterialProperties: [1×2 materialProperties]
Boundary Conditions
FaceBC: [0×11 faceBC]
EdgeBC: [0×20 edgeBC]
VertexBC: [0×12 vertexBC]
Loads
CellLoad: [0×2 cellLoad]
FaceLoad: [0×11 faceLoad]
EdgeLoad: [0×20 edgeLoad]
VertexLoad: [0×12 vertexLoad]
Initial Conditions
CellIC: [0×2 cellIC]
FaceIC: [0×11 faceIC]
EdgeIC: [0×20 edgeIC]
VertexIC: [0×12 vertexIC]
Other Parameters
DampingAlpha: 0
DampingBeta: 0
ReferenceTemperature: []
SolverOptions: [1×1 pde.PDESolverOptions]
Show all properties
The materialProperties function finds the names of the materials in a built-in catalog and assigns all properties for these materials from the catalog. By default, the toolbox displays only the properties for the specified analysis type. To display all properties, click Show all properties.
model.MaterialProperties
ans = 1×2 materialProperties array Properties for analysis type: structuralTransient Index PoissonsRatio YoungsModulus MassDensity ShearModulus 1 0.3080 1.2800e+11 8960 [] 2 0.3000 1.5000e+11 8.0000e+03 [] Show all properties
You can change values of the material properties imported from the catalog. The values in the catalog do not change.
model.MaterialProperties(1).PoissonsRatio = 0.35; model.MaterialProperties(2).YoungsModulus = 1.5e+11; model.MaterialProperties
ans = 1×2 materialProperties array Properties for analysis type: structuralTransient Index PoissonsRatio YoungsModulus MassDensity ShearModulus 1 0.3500 1.2800e+11 8960 [] 2 0.3000 1.5000e+11 8.0000e+03 [] Show all properties
If you change the analysis type, the toolbox displays the properties relevant to the new analysis type.
model.AnalysisType = "thermalTransient";
model.MaterialPropertiesans = 1×2 materialProperties array Properties for analysis type: thermalTransient Index ThermalConductivity MassDensity SpecificHeat 1 398 8960 380 2 11 8.0000e+03 515 Show all properties
All material properties in the catalog are in SI units. Ensure consistency with other specified values.
Specify relative permeability for an femodel object representing a magnetostatic problem.
Create an femodel object for solving a magnetostatic problem, and assign a geometry representing a plate with a hole to the model.
model = femodel(AnalysisType="magnetostatic", ... Geometry="PlateHolePlanar.stl");
Plot the geometry with the face labels.
pdegplot(model.Geometry,FaceLabels="on");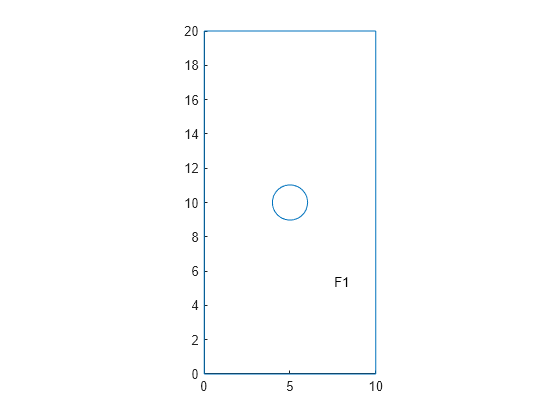
Specify the vacuum permeability value in the SI system of units.
model.MaterialProperties = materialProperties(RelativePermeability=5000); model.MaterialProperties
ans = 1×1 materialProperties array Properties for analysis type: magnetostatic Index RelativePermeability 1 5000 Show all properties
Specify Young's modulus, Poisson's ratio, and the mass density for an femodel object representing a static structural problem.
Create and plot a bimetallic beam geometry.
H = 0.1;
gm = multicuboid(0.5,0.1,[H,H],Zoffset=[0,H]);
pdegplot(gm,CellLabels="on");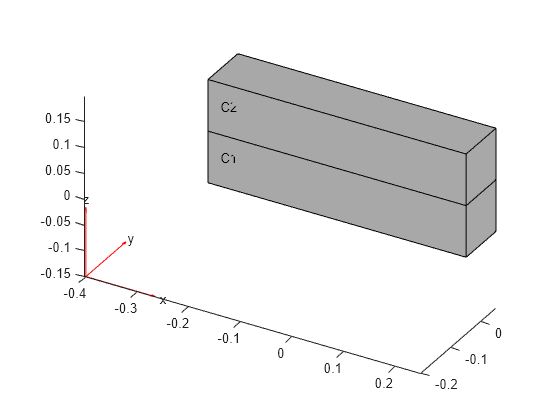
Create an femodel object for solving a static structural problem, and assign the geometry to the model.
model = femodel(AnalysisType="structuralStatic", ... Geometry=gm);
Specify different values of Young's modulus, Poisson's ratio, and the mass density for cells 1 and 2.
model.MaterialProperties(1) = materialProperties(YoungsModulus=210e9, ... PoissonsRatio=0.28, ... MassDensity=1.3e-5); model.MaterialProperties(2) = materialProperties(YoungsModulus=110e9, ... PoissonsRatio=0.37, ... MassDensity=2.4e-5); model.MaterialProperties
ans = 1×2 materialProperties array Properties for analysis type: structuralStatic Index CTE PoissonsRatio YoungsModulus MassDensity ShearModulus 1 [] 0.2800 2.1000e+11 1.3000e-05 [] 2 [] 0.3700 1.1000e+11 2.4000e-05 [] Show all properties
Use function handles to specify a thermal conductivity that depends on temperature and a specific heat that depends on coordinates.
Create a rectangular geometry.
gm = decsg([3 4 -1.5 1.5 1.5 -1.5 0 0 .2 .2]');
Create an femodel object for solving a transient thermal problem, and assign the geometry to the model.
model = femodel(AnalysisType="thermalTransient", ... Geometry=gm);
Specify the thermal conductivity as a linear function of temperature, k = 40 + 0.003T.
k = @(location,state)40 + 0.003*state.u;
Specify the specific heat as a linear function of the y-coordinate, cp = 500y.
cp = @(location,state)500*location.y;
Specify the thermal conductivity, mass density, and specific heat of the material.
model.MaterialProperties = materialProperties(ThermalConductivity=k, ... MassDensity=2.7*10^(-6), ... SpecificHeat=cp); model.MaterialProperties
ans = 1×1 materialProperties array Properties for analysis type: thermalTransient Index ThermalConductivity MassDensity SpecificHeat 1 @(location,state)40+0.003*state.u 2.7000e-06 @(location,state)500*location.y Show all properties
Use a function handle to specify a relative permeability that depends on the magnetic flux density.
Create an femodel object for solving a magnetostatic problem, and assign a geometry representing a plate with a hole to the model.
model = femodel(AnalysisType="magnetostatic", ... Geometry="PlateHolePlanar.stl");
Plot the geometry with the face labels.
pdegplot(model.Geometry,FaceLabels="on");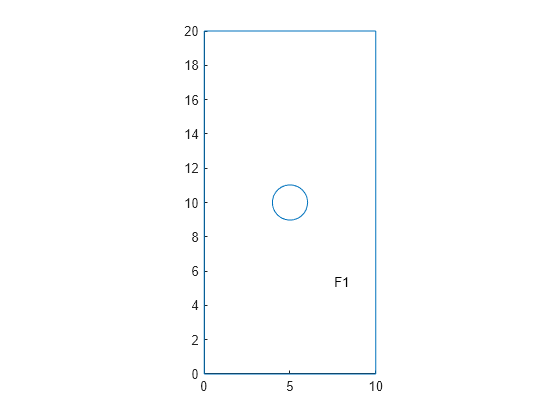
Specify the vacuum permeability value in the SI system of units.
model.VacuumPermeability = 1.2566370614e-6;
Specify the data for the magnetic flux density, B, and the corresponding magnetic field strength, H.
B = [0 .3 .8 1.12 1.32 1.46 1.54 1.61875 1.74]; H = [0 29.8 79.6 159.2 318.31 795.8 1591.6 3376.7 7957.8];
From the data for B and H, interpolate the H(B) dependency (B-H curve) using the modified Akima cubic Hermite interpolation method.
HofB = griddedInterpolant(B,H,"makima","linear"); muR = @(B) B./HofB(B)/mu0;
Specify the relative permeability that depends on the magnetic flux density.
model.MaterialProperties = materialProperties(RelativePermeability=muR); model.MaterialProperties
ans = 1×1 materialProperties array Properties for analysis type: magnetostatic Index RelativePermeability 1 @(B)B./HofB(B)/mu0 Show all properties
Use vector values to specify Young's modulus, Poisson's ratio, and shear modulus representing an orthotropic material.
Create an femodel object for solving a static structural problem, and assign a geometry representing a cube with a cylindrical hole to the model.
model = femodel(AnalysisType="structuralStatic", ... Geometry="BlockWithHole.step");
Plot the geometry.
pdegplot(model.Geometry,FaceAlpha=0.3);
Specify Young's modulus, Poisson's ratio, shear modulus, and the mass density. For an orthotropic material, all parameters, except the mass density, must be 1-by-3 vector of positive numbers.
E = [22E9,9.8E9,22E9]; nu = [0.28,0.28,0.11]; G = [3.5E9,3.5E9,2.5E9]; rho = 1.3e-5; model.MaterialProperties = materialProperties(YoungsModulus=E, ... PoissonsRatio=nu, ... ShearModulus=G, ... MassDensity=rho); model.MaterialProperties
ans = 1×1 materialProperties array Properties for analysis type: structuralStatic Index CTE PoissonsRatio YoungsModulus MassDensity ShearModulus 1 [] [0.2800 0.2800 0.1100] [2.2000e+10 9.8000e+09 2.2000e+10] 1.3000e-05 [3.5000e+09 3.5000e+09 2.5000e+09] Show all properties
Version History
Introduced in R2023amaterialProperties accepts material names, specified as strings such
as "teflon" or "copper", as arguments. The function
finds the specified material name in a built-in catalog and assigns all material properties
for this material from the catalog.
See Also
Functions
generateMesh|solve|pdegplot|pdemesh
Objects
femodel|fegeometry|edgeBC|faceBC|vertexBC|farFieldBC|cellLoad|faceLoad|edgeLoad|vertexLoad|cellIC|faceIC|edgeIC|vertexIC
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)