optimproblem
Create optimization problem
Description
Use optimproblem to create an optimization
problem.
Tip
For the full workflow, see Problem-Based Optimization Workflow.
prob = optimproblem(Name,Value)Name,Value pair
arguments. For example, to specify a maximization problem instead of a minimization
problem, use prob =
optimproblem('ObjectiveSense','maximize').
Note
All names in an optimization problem must be unique. Specifically, all variable names, objective function names, and constraint function names must be different.
Examples
Create an optimization problem with default properties.
prob = optimproblem
prob =
OptimizationProblem with properties:
Description: ''
ObjectiveSense: 'minimize'
Variables: [0×0 struct] containing 0 OptimizationVariables
Objective: [0×0 OptimizationExpression]
Constraints: [0×0 struct] containing 0 OptimizationConstraints
No problem defined.
Create a linear programming problem for maximization. The problem has two positive variables and three linear inequality constraints.
prob = optimproblem('ObjectiveSense','max');
Create positive variables. Include an objective function in the problem.
x = optimvar('x',2,1,'LowerBound',0); prob.Objective = x(1) + 2*x(2);
Create linear inequality constraints in the problem.
cons1 = x(1) + 5*x(2) <= 100; cons2 = x(1) + x(2) <= 40; cons3 = 2*x(1) + x(2)/2 <= 60; prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3;
Review the problem.
show(prob)
OptimizationProblem :
Solve for:
x
maximize :
x(1) + 2*x(2)
subject to cons1:
x(1) + 5*x(2) <= 100
subject to cons2:
x(1) + x(2) <= 40
subject to cons3:
2*x(1) + 0.5*x(2) <= 60
variable bounds:
0 <= x(1)
0 <= x(2)
Solve the problem.
sol = solve(prob);
Solving problem using linprog. Optimal solution found.
sol.x
ans = 2×1
25
15
Create a problem with two objective functions of a 2-D variable x. Create the objective functions as expressions in x, and place them in the objective as structures.
x = optimvar("x",2,LowerBound=-2,UpperBound=2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = norm(x - [1;0])^2;Solve the problem.
rng default % For reproducibility sol = solve(prob);
Solving problem using gamultiobj. gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
Plot the solution.
paretoplot(sol)

Examine one point on the Pareto front. To do so, click the figure and click the Data Tips tool:
![]()
Then click a point on the Pareto front.
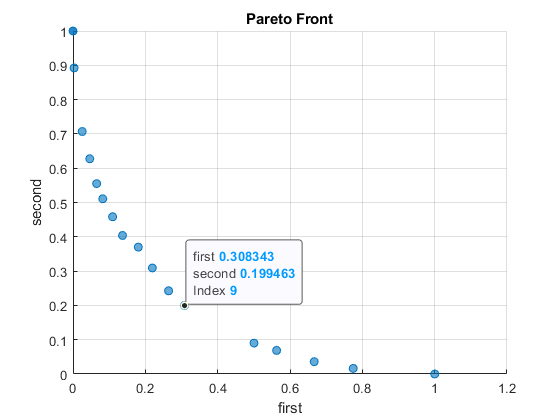
The index of the pictured point is 9. You can find the x value associated with this point as the solution with index 9.
sol(9).x
ans = 2×1
0.5544
-0.0306
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: To specify a maximization problem, use prob =
optimproblem('ObjectiveSense','maximize').
Problem constraints, specified as an OptimizationConstraint array or a structure with
OptimizationConstraint arrays as fields.
Example: prob = optimproblem('Constraints',sum(x,2) ==
1)
Problem label, specified as a string or character vector. The software does not use
Description for computation. Description is an
arbitrary label that you can use for any reason. For example, you can share, archive, or
present a model or problem, and store descriptive information about the model or problem
in Description.
Example: "An iterative approach to the Traveling Salesman problem"
Data Types: char | string
Objective function, specified as a scalar OptimizationExpression object, an array of
OptimizationExpression objects, or a structure
with scalar OptimizationExpression as fields.
For a scalar (single-objective) problem, specify the objective function as a scalar optimization expression or as a structure with a scalar optimization expression as the value.
For a multiobjective problem, specify the objective functions as a vector-valued optimization expression, as an array of optimization expressions, or as a structure of optimization expressions. For example, this objective is a structure of optimization expressions in a scalar optimization variable
x:prob = optimproblem; prob.Objective.first = x^2; prob.Objective.second = (x + 1)^2;
Example: prob =
optimproblem('Objective',sum(sum(x))) for a 2-D variable
x.
Example: prob = optimproblem('Objective',(x-a).^2)
where x and a have size 2-by-1,
and x is an optimization variable.
Sense of optimization, specified as 'minimize' or
'maximize'. You can also specify
'min' to obtain 'minimize' or
'max' to obtain 'maximize'.
The solve function minimizes an objective when
ObjectiveSense is 'minimize'
and maximizes an objective when ObjectiveSense is
'maximize'.
ObjectiveSense can be a structure with values
'minimize', 'min',
'maximize', or 'max'. You can
use this form when the problem objective is a structure. The
Objective and ObjectiveSense
structures should have the same field names, so the
ObjectiveSense applies to the corresponding
Objective. For example,
x = optimvar('x',2,"UpperBound",2,"LowerBound",-2); prob = optimproblem; prob.Objective.first = norm(x)^2; prob.Objective.second = -norm(x - [1;0])^2; prob.ObjectiveSense.first = "min"; prob.ObjectiveSense.second = "max";
If Objective is a structure, you can specify
ObjectiveSense as a name such as
'max'. In this case, all objectives have the same
ObjectiveSense.
Example: prob =
optimproblem('ObjectiveSense','max')
Data Types: char | string
Output Arguments
Optimization problem, returned as an OptimizationProblem object. Typically, to complete the problem
description, you specify an objective function and constraints. However, you
can have a feasibility problem, which has no objective function, or you can
have a problem with no constraints. Solve a complete problem by calling
solve.
Warning
The problem-based approach does not support complex values in the following: an objective function, nonlinear equalities, and nonlinear inequalities. If a function calculation has a complex value, even as an intermediate value, the final result might be incorrect.
Version History
Introduced in R2017b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)