fminsearch
Search for local minimum of unconstrained multivariable function using derivative-free method
Syntax
Description
Nonlinear programming solver. Searches for a local minimum of a problem specified by
f(x) is a function that returns a scalar, and x is a vector or array.
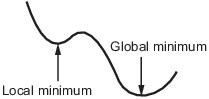
For details, see Local vs. Global Minimum.
Examples
Input Arguments
Output Arguments
More About
Tips
fminsearchonly minimizes over the real numbers, that is, the vector or array x must only consist of real numbers and f(x) must only return real numbers. When x has complex values, split x into real and imaginary parts.Use
fminsearchto solve nondifferentiable problems or problems with discontinuities, particularly if no discontinuity occurs near the solution.
Algorithms
fminsearch uses the simplex search method
of Lagarias et al. [1]. This is a direct search method that does not use numerical
or analytic gradients as in fminunc (Optimization Toolbox).
The algorithm is described in detail in fminsearch Algorithm.
The algorithm is not guaranteed to converge to a local minimum.
Alternative Functionality
App
The Optimize Live
Editor task provides a visual interface for fminsearch.
References
[1] Lagarias, J. C., J. A. Reeds, M. H. Wright, and P. E. Wright. “Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions.” SIAM Journal of Optimization. Vol. 9, Number 1, 1998, pp. 112–147.
Extended Capabilities
Version History
Introduced before R2006a