fminunc
Find minimum of unconstrained multivariable function
Syntax
Description
Nonlinear programming solver.
Finds the minimum of a problem specified by
where f(x) is a function that returns a scalar.
x is a vector or a matrix; see Matrix Arguments.
x = fminunc(fun,x0)x0 and attempts to find a local minimum x of
the function described in fun. The point x0 can
be a scalar, vector, or matrix.
Note
Passing Extra Parameters explains how to pass extra parameters to the objective function and nonlinear constraint functions, if necessary.
fminunc is for nonlinear problems without
constraints. If your problem has constraints, generally use fmincon. See Optimization Decision Table.
x = fminunc(fun,x0,options)fun with
the optimization options specified in options.
Use optimoptions to set these
options.
Examples
Minimize the function .
To do so, write an anonymous function fun that calculates the objective.
fun = @(x)3*x(1)^2 + 2*x(1)*x(2) + x(2)^2 - 4*x(1) + 5*x(2);
Call fminunc to find a minimum of fun near [1,1].
x0 = [1,1]; [x,fval] = fminunc(fun,x0)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
x = 1×2
2.2500 -4.7500
fval = -16.3750
fminunc can be faster and more reliable when you provide derivatives.
Write an objective function that returns the gradient as well as the function value. Use the conditionalized form described in Including Gradients and Hessians. The objective function is Rosenbrock's function,
which has gradient
.
The code for the objective function with gradient appears at the end of this example.
Create options to use the objective function’s gradient. Also, set the algorithm to 'trust-region'.
options = optimoptions('fminunc','Algorithm','trust-region','SpecifyObjectiveGradient',true);
Set the initial point to [-1,2]. Then call fminunc.
x0 = [-1,2]; fun = @rosenbrockwithgrad; x = fminunc(fun,x0,options)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
x = 1×2
1.0000 1.0000
The following code creates the rosenbrockwithgrad function, which includes the gradient as the second output.
function [f,g] = rosenbrockwithgrad(x) % Calculate objective f f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2; if nargout > 1 % gradient required g = [-400*(x(2)-x(1)^2)*x(1) - 2*(1-x(1)); 200*(x(2)-x(1)^2)]; end end
Solve the same problem as in Supply Gradient using a problem structure instead of separate arguments.
Write an objective function that returns the gradient as well as the function value. Use the conditionalized form described in Including Gradients and Hessians. The objective function is Rosenbrock's function,
,
which has gradient
.
The code for the objective function with gradient appears at the end of this example.
Create options to use the objective function’s gradient. Also, set the algorithm to 'trust-region'.
options = optimoptions('fminunc','Algorithm','trust-region','SpecifyObjectiveGradient',true);
Create a problem structure including the initial point x0 = [-1,2]. For the required fields in this structure, see problem.
problem.options = options;
problem.x0 = [-1,2];
problem.objective = @rosenbrockwithgrad;
problem.solver = 'fminunc';Solve the problem.
x = fminunc(problem)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
x = 1×2
1.0000 1.0000
The following code creates the rosenbrockwithgrad function, which includes the gradient as the second output.
function [f,g] = rosenbrockwithgrad(x) % Calculate objective f f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2; if nargout > 1 % gradient required g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1)); 200*(x(2)-x(1)^2)]; end end
Find both the location of the minimum of a nonlinear function and the value of the function at that minimum. The objective function is
.
fun = @(x)x(1)*exp(-(x(1)^2 + x(2)^2)) + (x(1)^2 + x(2)^2)/20;
Find the location and objective function value of the minimizer starting at x0 = [1,2].
x0 = [1,2]; [x,fval] = fminunc(fun,x0)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
x = 1×2
-0.6691 0.0000
fval = -0.4052
Choose fminunc options and outputs to examine the solution process.
Set options to obtain iterative display and use the 'quasi-newton' algorithm.
options = optimoptions(@fminunc,'Display','iter','Algorithm','quasi-newton');
The objective function is
fun = @(x)x(1)*exp(-(x(1)^2 + x(2)^2)) + (x(1)^2 + x(2)^2)/20;
Start the minimization at x0 = [1,2], and obtain outputs that enable you to examine the solution quality and process.
x0 = [1,2]; [x,fval,exitflag,output] = fminunc(fun,x0,options)
First-order
Iteration Func-count f(x) Step-size optimality
0 3 0.256738 0.173
1 6 0.222149 1 0.131
2 9 0.15717 1 0.158
3 18 -0.227902 0.438133 0.386
4 21 -0.299271 1 0.46
5 30 -0.404028 0.102071 0.0458
6 33 -0.404868 1 0.0296
7 36 -0.405236 1 0.00119
8 39 -0.405237 1 0.000252
9 42 -0.405237 1 7.97e-07
Local minimum found.
Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.
<stopping criteria details>
x = 1×2
-0.6691 0.0000
fval = -0.4052
exitflag = 1
output = struct with fields:
iterations: 9
funcCount: 42
stepsize: 2.9343e-04
lssteplength: 1
firstorderopt: 7.9721e-07
algorithm: 'quasi-newton'
message: 'Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 6.796073e-07, is less ↵than options.OptimalityTolerance = 1.000000e-06.'
The exit flag
1shows that the solution is a local optimum.The
outputstructure shows the number of iterations, number of function evaluations, and other information.The iterative display also shows the number of iterations and function evaluations.
When your problem has a large number of variables, the
default value of the HessianApproximation can cause
fminunc to use a large amount of memory and run slowly.
To use less memory and run faster, specify
HessianApproximation="lbfgs".
For example, if you attempt to minimize the multirosenbrock
function (listed below) with 1e5 variables using the default parameters,
fminunc issues an error.
N = 1e5; x0 = -2*ones(N,1); x0(2:2:N) = 2; [x,fval] = fminunc(@multirosenbrock,x0)
Error using eye
Requested 100000x100000 (74.5GB) array exceeds maximum array size preference (63.9GB). This might cause MATLAB to become
unresponsive.
Error in optim.internal.fminunc.AbstractDenseHessianApproximation (line 21)
this.Value = eye(nVars);
Error in optim.internal.fminunc.BFGSHessianApproximation (line 14)
this = this@optim.internal.fminunc.AbstractDenseHessianApproximation(nVars);
Error in fminusub (line 73)
HessApprox = optim.internal.fminunc.BFGSHessianApproximation(sizes.nVar);
Error in fminunc (line 488)
[x,FVAL,GRAD,HESSIAN,EXITFLAG,OUTPUT] = fminusub(funfcn,x, ...To solve this problem, set the HessianApproximation
option to "lbfgs". To speed the solution, set options to
use the supplied gradient.
N = 1e5; x0 = -2*ones(N,1); x0(2:2:N) = 2; options = optimoptions("fminunc",HessianApproximation="lbfgs",... SpecifyObjectiveGradient=true); [x,fval] = fminunc(@multirosenbrock,x0,options);
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance.
The theoretical solution is x(i) = 1 for all
i. Check the accuracy of the returned
solution.
max(abs(x-1))
ans = 1.3795e-04
This code creates the multirosenbrock function.
function [f,g] = multirosenbrock(x) % Get the problem size n = length(x); if n == 0, error('Input vector, x, is empty.'); end if mod(n,2) ~= 0 error('Input vector, x ,must have an even number of components.'); end % Evaluate the vector function odds = 1:2:n; evens = 2:2:n; F = zeros(n,1); F(odds,1) = 1-x(odds); F(evens,1) = 10.*(x(evens)-x(odds).^2); f = sum(F.^2); if nargout >= 2 % Calculate gradient g = zeros(n,1); g(evens) = 200*(x(evens)-x(odds).^2); g(odds) = -2*(1 - x(odds)) - 400*(x(evens)-x(odds).^2).*x(odds); end end
Input Arguments
Function to minimize, specified as a function handle or function
name. fun is a function that accepts a vector or
array x and returns a real scalar f,
the objective function evaluated at x.
fminunc passes x to your objective function in the shape of the x0 argument. For example, if x0 is a 5-by-3 array, then fminunc passes x to fun as a 5-by-3 array.
Specify fun as a function handle for a file:
x = fminunc(@myfun,x0)
where myfun is a MATLAB® function such
as
function f = myfun(x) f = ... % Compute function value at x
You can also specify fun as a function handle
for an anonymous function:
x = fminunc(@(x)norm(x)^2,x0);
If you can compute the gradient of fun
and the SpecifyObjectiveGradient
option is set to true, as set
by
options = optimoptions('fminunc','SpecifyObjectiveGradient',true)
fun must return the gradient vector
g(x) in the second output argument.If you can also compute the Hessian matrix and the HessianFcn option
is set to 'objective' via options = optimoptions('fminunc','HessianFcn','objective') and the Algorithm option
is set to 'trust-region', fun must
return the Hessian value H(x), a symmetric matrix,
in a third output argument. fun can give a sparse
Hessian. See Hessian for fminunc trust-region or fmincon trust-region-reflective algorithms for
details.
The trust-region algorithm allows you to
supply a Hessian multiply function. This function gives the result
of a Hessian-times-vector product without computing the Hessian directly.
This can save memory. See Hessian Multiply Function.
Example: fun = @(x)sin(x(1))*cos(x(2))
Data Types: char | function_handle | string
Initial point, specified as a real vector or real array. Solvers use the number of elements in
x0 and the size of x0 to determine the number
and size of variables that fun accepts.
Example: x0 = [1,2,3,4]
Data Types: double
Optimization options, specified as the output of optimoptions or
a structure such as optimset returns.
Some options apply to all algorithms, and others are relevant for particular algorithms. See Optimization Options Reference for detailed information.
Some options are absent from the
optimoptions display. These options appear in italics in the following
table. For details, see View Optimization Options.
| All Algorithms | |
| Choose the The |
| CheckGradients | Compare user-supplied derivatives (gradient of objective) to
finite-differencing derivatives. Choices are
For
The |
| Diagnostics | Display diagnostic information
about the function to be minimized or solved. Choices are |
| DiffMaxChange | Maximum change in variables for
finite-difference gradients (a positive scalar). The default is |
| DiffMinChange | Minimum change in variables for
finite-difference gradients (a positive scalar). The default is |
Display | Level of display (see Iterative Display):
|
FiniteDifferenceStepSize | Scalar or vector step size factor for finite differences. When
you set
sign′(x) = sign(x) except sign′(0) = 1.
Central finite differences are
FiniteDifferenceStepSize expands to a vector. The default
is sqrt(eps) for forward finite differences, and eps^(1/3)
for central finite differences.The
trust-region algorithm uses For |
FiniteDifferenceType | Finite differences, used to estimate
gradients, are either For |
| FunValCheck | Check whether objective function
values are valid. The default setting, |
MaxFunctionEvaluations | Maximum number of function evaluations allowed, a nonnegative
integer. The default value is
For |
MaxIterations | Maximum number of iterations allowed, a nonnegative integer. The
default value is For |
OptimalityTolerance | Termination tolerance on the first-order optimality (a
nonnegative scalar). The default is For |
OutputFcn | Specify one or more user-defined functions that an optimization
function calls at each iteration. Pass a function handle
or a cell array of function handles. The default is none
( |
PlotFcn | Plots various measures of progress while the algorithm executes;
select from predefined plots or write your own. Pass a
built-in plot function name, a function handle, or a
cell array of built-in plot function names or function
handles. For custom plot functions, pass function
handles. The default is none
(
Custom plot functions use the same syntax as output functions. See Output Functions for Optimization Toolbox and Output Function and Plot Function Syntax. For
|
SpecifyObjectiveGradient | Gradient for the objective function
defined by the user. See the description of For |
StepTolerance | Termination tolerance on For |
TypicalX | Typical The |
trust-region Algorithm | |
FunctionTolerance | Termination tolerance on the function value, a nonnegative
scalar. The default is For |
HessianFcn | If set to If set to For |
HessianMultiplyFcn | Hessian multiply function, specified as a function handle. For
large-scale structured problems, this function computes
the Hessian matrix product W = hmfun(Hinfo,Y) where
The first
argument is the same as the third argument returned by
the objective function [f,g,Hinfo] = fun(x)
Note To use the For an example, see Minimization with Dense Structured Hessian, Linear Equalities. For |
| HessPattern | Sparsity pattern of the Hessian
for finite differencing. Set Use When the structure is unknown,
do not set |
| MaxPCGIter | Maximum number of preconditioned
conjugate gradient (PCG) iterations, a positive scalar. The default
is |
| PrecondBandWidth | Upper bandwidth of preconditioner
for PCG, a nonnegative integer. By default, |
SubproblemAlgorithm | Determines how the iteration step
is calculated. The default, |
| TolPCG | Termination tolerance on the PCG
iteration, a positive scalar. The default is |
quasi-newton Algorithm | |
HessianApproximation | Specifies how
The choice For Note Usually, the |
ObjectiveLimit | A tolerance (stopping criterion)
that is a scalar. If the objective function value at an iteration
is less than or equal to |
UseParallel | When |
Example: options = optimoptions('fminunc','SpecifyObjectiveGradient',true)
Problem structure, specified as a structure with the following fields:
| Field Name | Entry |
|---|---|
| Objective function |
| Initial point for x |
| 'fminunc' |
| Options created with optimoptions |
Data Types: struct
Output Arguments
Solution, returned as a real vector or real array. The size
of x is the same as the size of x0.
Typically, x is a local solution to the problem
when exitflag is positive. For information on
the quality of the solution, see When the Solver Succeeds.
Objective function value at the solution, returned as a real
number. Generally, fval = fun(x).
Reason fminunc stopped, returned as an
integer.
| Magnitude of gradient is smaller than the |
| Change in |
| Change in the objective function value was less than
the |
| Predicted decrease in the objective function was less
than the |
| Number of iterations exceeded |
| Algorithm was terminated by the output function. |
| Objective function at current iteration went below |
Information about the optimization process, returned as a structure with fields:
iterations | Number of iterations taken |
funcCount | Number of function evaluations |
firstorderopt | Measure of first-order optimality |
algorithm | Optimization algorithm used |
cgiterations | Total number of PCG iterations ( |
lssteplength | Size of line search step relative to search direction
( |
stepsize | Final displacement in |
message | Exit message |
Gradient at the solution, returned as a real vector. grad gives
the gradient of fun at the point x(:).
Approximate Hessian, returned as a real matrix. For the meaning of
hessian, see Hessian Output.
If the HessianApproximation option is
"lbfgs" or {"lbfgs" n} then the
returned hessian is [].
Data Types: double
More About
The next few items list the possible enhanced exit messages from
fminunc. Enhanced exit messages give a link for more
information as the first sentence of the message.
The solver located a point that seems to be a local minimum, since the First-Order Optimality Measure is less than the OptimalityTolerance tolerance.
For suggestions on how to proceed, see When the Solver Succeeds.
The initial point seems to be a local minimum because the First-Order Optimality Measure is less than the OptimalityTolerance tolerance.
For suggestions on how to proceed, see Final Point Equals Initial Point.
The solver may have reached a local minimum, but cannot be certain because the First-Order Optimality Measure is not less than the OptimalityTolerance tolerance.
For suggestions on how to proceed, see Local Minimum Possible.
The solver stopped because it reached a limit on the number of iterations or function evaluations before it minimized the objective to the requested tolerance.
For suggestions on how to proceed, see Too Many Iterations or Function Evaluations.
The solver reached a feasible point whose objective function value was less than or equal to the ObjectiveLimit tolerance. The problem is unbounded, or poorly scaled, or the ObjectiveLimit option is too high.
For suggestions on how to proceed, see Problem Unbounded.
The 'trust-region' algorithm requires that you provide a
gradient in the objective function and set the
SpecifyObjectiveGradient option to
true.
To proceed, do one of the following:
Set the
Algorithmoption to'quasi-newton'.Ensure that your objective function provides a gradient and set the
SpecifyObjectiveGradientoption totrue. See Including Gradients and Hessians.
The next few items contain definitions for terms in the fminunc exit messages.
Generally, a tolerance is a threshold which, if crossed, stops the iterations of a solver. For more information on tolerances, see Tolerances and Stopping Criteria.
A local minimum of a function is a point where the function value is smaller than at nearby points, but possibly greater than at a distant point.
A global minimum is a point where the function value is smaller than at all other feasible points.
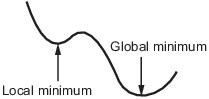
Solvers try to find a local minimum. The result can be a global minimum. For more information, see Local vs. Global Optima.
The first-order optimality measure is the maximum of the absolute value of the components of the gradient vector (also known as the infinity norm of the gradient). This should be zero at a minimizing point.
For more information, see First-Order Optimality Measure.
The size of the gradient is the maximum of the absolute value of the components of the gradient vector (also known as the infinity norm). This should be zero at a minimizing point.
For more information, see First-Order Optimality Measure.
The tolerance called OptimalityTolerance relates to the
first-order optimality measure. Iterations end when the first-order optimality
measure is less than OptimalityTolerance.
The first-order optimality measure of an unconstrained problem is the maximum of the absolute value of the components of the gradient vector (also known as the infinity norm of the gradient). This should be zero at a minimizing point.
For more information, see First-Order Optimality Measure.
FunctionTolerance is a tolerance for the size of
the latest change in objective function value.

StepTolerance is a tolerance for the size of
the last step, meaning the size of the change in location where the objective
function was evaluated.

The norm of the current step is the size of the change in location where the objective function was evaluated.
For more information, see Tolerances and Stopping Criteria.
The solver reached a feasible point whose objective function value was less than or equal to the ObjectiveLimit tolerance. The problem is unbounded, or poorly scaled, or the ObjectiveLimit option is too high.
For suggestions on how to proceed, see Problem Unbounded.
The line search interval is the line segment along the search direction in which the solver attempts to minimize the objective function. If this interval is too small, the solver exits. The solver calculates the search direction and the size of this interval according to various algorithms described in Unconstrained Nonlinear Optimization Algorithms.
An output function (or plot function) is evaluated once per iteration of a solver. It can report many optimization quantities during the course of a solver's progress, and can halt the solver.
For more information, see Output Functions for Optimization Toolbox or Plot Functions.
MaxIterations is a tolerance on the number of iterations the solver performs. When the solver has taken MaxIterations iterations, the iterations end.
For more information, see Iterations and Function Counts or Tolerances and Stopping Criteria.
MaxFunctionEvaluations is a tolerance on the number of points where the solver evaluates the objective and/or constraint functions. When the solver has evaluated functions at MaxFunctionEvaluations points, the iterations end.
For more information, see Iterations and Function Counts or Tolerances and Stopping Criteria.
The search direction is the vector from the current point along which the solver looks for an improvement. Optimization Toolbox™ solvers compute search directions via various algorithms, described in Unconstrained Nonlinear Optimization Algorithms.
Algorithms
By default, the quasi-newton algorithm uses the BFGS Quasi-Newton method
with a cubic line search procedure. This quasi-Newton method uses the BFGS ([1],[5],[8], and [9]) formula for updating the approximation of
the Hessian matrix. You can also specify the low-memory BFGS algorithm
("lbfgs") as the HessianApproximation
option. While not recommended, you can specify the DFP ([4],[6], and [7]) formula, which approximates the inverse Hessian matrix, by setting
the option to 'dfp'. You can specify a steepest descent method by
setting the option to 'steepdesc', although this setting is
usually inefficient. See fminunc quasi-newton Algorithm.
The trust-region algorithm requires that
you supply the gradient in fun and
set SpecifyObjectiveGradient to true using optimoptions. This algorithm is a subspace
trust-region method and is based on the interior-reflective Newton
method described in [2] and [3]. Each iteration involves the approximate
solution of a large linear system using the method of preconditioned
conjugate gradients (PCG). See fminunc trust-region Algorithm, Trust-Region Methods for Nonlinear Minimization and Preconditioned Conjugate Gradient Method.
Alternative Functionality
App
The Optimize Live Editor task provides a visual interface for fminunc.
References
[1] Broyden, C. G. “The Convergence of a Class of Double-Rank Minimization Algorithms.” Journal Inst. Math. Applic., Vol. 6, 1970, pp. 76–90.
[2] Coleman, T. F. and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds.” SIAM Journal on Optimization, Vol. 6, 1996, pp. 418–445.
[3] Coleman, T. F. and Y. Li. “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds.” Mathematical Programming, Vol. 67, Number 2, 1994, pp. 189–224.
[4] Davidon, W. C. “Variable Metric Method for Minimization.” A.E.C. Research and Development Report, ANL-5990, 1959.
[5] Fletcher, R. “A New Approach to Variable Metric Algorithms.” Computer Journal, Vol. 13, 1970, pp. 317–322.
[6] Fletcher, R. “Practical Methods of Optimization.” Vol. 1, Unconstrained Optimization, John Wiley and Sons, 1980.
[7] Fletcher, R. and M. J. D. Powell. “A Rapidly Convergent Descent Method for Minimization.” Computer Journal, Vol. 6, 1963, pp. 163–168.
[8] Goldfarb, D. “A Family of Variable Metric Updates Derived by Variational Means.” Mathematics of Computing, Vol. 24, 1970, pp. 23–26.
[9] Shanno, D. F. “Conditioning of Quasi-Newton Methods for Function Minimization.” Mathematics of Computing, Vol. 24, 1970, pp. 647–656.
Extended Capabilities
To run in parallel, set the 'UseParallel' option to true.
options = optimoptions('solvername','UseParallel',true)
For more information, see Using Parallel Computing in Optimization Toolbox.
Version History
Introduced before R2006aThe CheckGradients option will be removed in a future release. To check the first derivatives of objective functions or nonlinear constraint functions, use the checkGradients function.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)