uniquetol

Unique values within tolerance

Syntax

C = uniquetol(A,tol)

C = uniquetol(A)

C = uniquetol(A,___,occurrence)

[___] = uniquetol(___,Name=Value)

[C,IA,IC] = uniquetol(___)

Description

C = uniquetol(A,tol) returns the unique elements in A using tolerance tol. Two values, u and v, are within tolerance if

abs(u-v) <= tol*max(abs(A(:)))

That is, uniquetol scales tol input based on the magnitude of the data.

uniquetol is similar to unique. unique performs exact comparisons, while uniquetol performs comparisons using a tolerance.

C = uniquetol(A) uses a default tolerance of 1e-6 for single-precision inputs and 1e-12 for double-precision inputs.

C = uniquetol(A,___,occurrence) specifies whether to select the highest or lowest value as being unique when several values are within tolerance of each other. You can specify occurrence for either of the previous syntaxes.

[___] = uniquetol(___,Name=Value) specifies additional parameters for determining the unique elements using one or more name-value arguments. For example, uniquetol(A,ByRows=true) determines the unique rows in A.

[C,IA,IC] = uniquetol(___) returns index vectors IA and IC. C = A(IA) and A~C(IC) (or A(:)~C(IC) if A is a matrix), where ~ means the values are within tolerance of each other.

Examples

Unique Elements in Presence of Numerical Error

Create a vector x. Obtain a second vector y by transforming and untransforming x. This transformation introduces round-off differences in y.

x = (1:6)'*pi;
y = 10.^log10(x);

Verify that x and y are not identical by taking the difference.

x-y

ans = 6×1
10-14 ×

    0.0444
         0
         0
         0
         0
   -0.3553

Concatenate the vectors x and y. Then, use unique to find the unique elements. The unique function performs exact comparisons and determines that some values in x are not exactly equal to values in y. These are the same elements that have a nonzero difference in x-y. Thus, C contains values that appear to be duplicates.

A = [x; y];
C = unique(A)

C = 8×1

    3.1416
    3.1416
    6.2832
    9.4248
   12.5664
   15.7080
   18.8496
   18.8496

Use uniquetol to perform the comparison using a small tolerance. uniquetol treats elements that are within tolerance as equal.

Ctol = uniquetol(A)

Ctol = 6×1

    3.1416
    6.2832
    9.4248
   12.5664
   15.7080
   18.8496

Determine Unique Rows

By default, uniquetol looks for unique elements that are within tolerance, but it also can find unique rows of a matrix that are within tolerance.

Create a numeric matrix, x. Obtain a second matrix, y, by transforming and untransforming x. This transformation introduces round-off differences to y.

x = [0.05 0.11 0.18; 0.18 0.21 0.29; 0.34 0.36 0.41; 0.46 0.52 0.76];
y = log10(10.^x);

Concatenate the matrices x and y. Then, use unique to find the unique rows. The unique function performs exact comparisons and determines that all of the rows in the concatenated matrix [x; y] are unique, even though some of the rows differ by only a small amount.

A = [x; y];
C = unique(A,"rows")

C = 8×3

    0.0500    0.1100    0.1800
    0.0500    0.1100    0.1800
    0.1800    0.2100    0.2900
    0.1800    0.2100    0.2900
    0.3400    0.3600    0.4100
    0.3400    0.3600    0.4100
    0.4600    0.5200    0.7600
    0.4600    0.5200    0.7600

Use uniquetol to find the unique rows. uniquetol treats rows that are within tolerance as equal.

Ctol = uniquetol(A,ByRows=true)

Ctol = 4×3

    0.0500    0.1100    0.1800
    0.1800    0.2100    0.2900
    0.3400    0.3600    0.4100
    0.4600    0.5200    0.7600

Prepare Vectors for Exact Comparison

Create a vector, x. Obtain a second vector, y, by transforming and untransforming x. This transformation introduces round-off differences to some elements in y.

x = (1:5)'*pi;
y = 10.^log10(x);

Concatenate the vectors x and y. Then, use uniquetol to reconstruct A, treating the values that are within tolerance as equal.

A = [x; y];
[C,IA,IC] = uniquetol(A);
newA = C(IC)

newA = 10×1

    3.1416
    6.2832
    9.4248
   12.5664
   15.7080
    3.1416
    6.2832
    9.4248
   12.5664
   15.7080

You can use newA with == or functions that use exact equality like isequal or unique in subsequent code.

D1 = unique(A)

D1 = 6×1

    3.1416
    3.1416
    6.2832
    9.4248
   12.5664
   15.7080

D2 = unique(newA)

D2 = 5×1

    3.1416
    6.2832
    9.4248
   12.5664
   15.7080

Control Selection of Unique Values

Control which elements uniquetol selects as being unique by specifying the occurrence option.

Create a vector and find which elements are unique within a tolerance of 1e-1.

A = [1 1.1 1.11 1.12 1.13 2];
C = uniquetol(A,1e-1)

C = 1×2

     1     2

Since the first five elements in A all have similar values with respect to the tolerance of 1e-1, only the lowest value among them is selected as being unique. This is because uniquetol begins with the lowest value in a and does not find a new element that is not within tolerance until the 2 at the end of the vector.

Use the "highest" option to specify that uniquetol should begin with the highest value in A. Now, the 1.13 element is selected as being unique since uniquetol works down from the highest values.

C2 = uniquetol(A,1e-1,"highest")

C2 = 1×2

    1.1300    2.0000

Subset Data Using Large Tolerance

Create a cloud of 2-D sample points constrained to be inside a circle of radius 0.5 centered at the point $$(\frac{1}{2},\frac{1}{2})$$.

x = rand(10000,2); 
insideCircle = sqrt((x(:,1)-.5).^2+(x(:,2)-.5).^2)<0.5;
A = x(insideCircle,:);

Find a reduced set of points, such that each point of the original dataset is within tolerance of a point.

tol = 0.05;
C = uniquetol(A,tol,ByRows=true);

Plot the original data set and the reduced set of points. All of the points in the reduced set are members of the original data set and are at least a distance tol apart.

plot(A(:,1),A(:,2),"c.")
hold on
axis equal
plot(C(:,1),C(:,2),"r.",MarkerSize=10)
legend("Original Data","Reduced Data")

Average Similar Values in Vector

Create a vector of random numbers and determine the unique elements using a tolerance. Specify OutputAllIndices as true to return all of the indices for the elements that are within tolerance of the unique values.

rng default
A = rand(100,1);
[C,IA] = uniquetol(A,1e-2,OutputAllIndices=true);

Find the average value of the elements that are within tolerance of the value C(2).

C(2)

ans = 
0.0318

allA = A(IA{2})

allA = 3×1

    0.0357
    0.0318
    0.0344

aveA = mean(allA)

aveA = 
0.0340

Specify Absolute Tolerance

By default, uniquetol uses a tolerance test of the form abs(u-v) <= tol*DS, where DS automatically scales based on the magnitude of the input data. You can specify a different DS value to use with the DataScale name-value argument. However, absolute tolerances (where DS is a scalar) do not scale based on the magnitude of the input data.

First, compare two small values that are a distance eps apart. Specify tol and DS to make the within tolerance equation: abs(u-v) <= 10^-6.

x = 0.1;
uniquetol([x exp(log(x))],10^-6,DataScale=1)

ans = 
0.1000

Next, increase the magnitude of the values. The round-off error in the calculation exp(log(x)) is proportional to the magnitude of the values, specifically to eps(x). Even though the two large values are a distance eps from one another, eps(x) is now much larger. Therefore, 10^-6 is no longer a suitable tolerance.

x = 10^10;
uniquetol([x exp(log(x))],10^-6,DataScale=1)

ans = 1×2
1010 ×

    1.0000    1.0000

Correct this issue by using the default (scaled) value of DS.

format long
Y = [0.1 10^10];
uniquetol([Y exp(log(Y))])

ans = 1×2
1010 ×

   0.000000000010000   1.000000000000000

Specify Scale of Data by Column

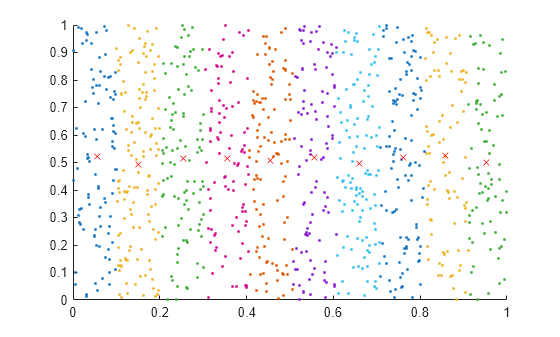
Create a set of random 2-D points, then use uniquetol to group the points into vertical bands that have a similar (within tolerance) x-coordinate. Use these options with uniquetol:

• Specify ByRows as true since the point coordinates are in the rows of A.

• Specify OutputAllIndices as true to return the indices for all points that have an x-coordinate within tolerance of each other.

• Specify DataScale as [1 Inf] to use an absolute tolerance for the x-coordinate while ignoring the y-coordinate.

A = rand(1000,2);
DS = [1 Inf];
[C,IA] = uniquetol(A,0.1,ByRows=true,OutputAllIndices=true,DataScale=DS);

Plot the points and average value for each band.

hold on
for k = 1:length(IA)
    plot(A(IA{k},1),A(IA{k},2),".")
    meanAi = mean(A(IA{k},:));
    plot(meanAi(1),meanAi(2),"xr")
end

Input Arguments

A — Query array

array

Query array, specified as a real and full array.

Data Types: single | double

tol — Comparison tolerance

positive real scalar

Comparison tolerance, specified as a positive real scalar. uniquetol scales the tol input using the maximum absolute value in input array A. Then uniquetol uses the resulting scaled comparison tolerance to determine which elements in A are unique. If two elements in A are within tolerance of each other, then uniquetol considers them to be equal.

Two values, u and v, are within tolerance if abs(u-v) <= tol*max(abs(A)).

To specify an absolute tolerance, specify both tol and the DataScale name-value argument.

Example: 0.05

Example: 1e-8

Example: eps

Data Types: single | double

occurrence — Occurrence of unique values

"lowest" (default) | "highest"

Occurrence of unique values, specified as one of the options in this table. The value of occurrence determines which elements uniquetol selects as being unique.

Option	Description
"lowest"	uniquetol starts with the lowest value in A, then repeatedly finds the next lowest value in A that is not within tolerance of any other value in C. The effect of this is that when several input values are within tolerance of each other, the lowest one is selected as being unique.
"highest"	uniquetol starts with the highest value in A, then repeatedly finds the next highest value in A that is not within tolerance of any other value in C. The effect of this is that when several input values are within tolerance of each other, the highest one is selected as being unique.

Example: C = uniquetol(A,tol,"highest")

Example: C = uniquetol([1 2 3],2,"highest") returns 3, since uniquetol starts with the highest value in the input and all other values are within tolerance.

Data Types: string | char

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: C = uniquetol(A,ByRows=true)

OutputAllIndices — Return all indices for repeated elements

false or 0 (default) | true or 1

Whether to return all indices for repeated elements, specified as logical 0 (false) or 1 (true).

When OutputAllIndices is false, IA is a column vector that contains indices to the first occurrence of repeated elements.

When OutputAllIndices is true, IA is a cell array that contains the indices for all elements in A that are within tolerance of a value in C. Each cell in IA corresponds to a value in C, and the values in each cell correspond to locations in A.

Example: [C,IA] = uniquetol(A,tol,OutputAllIndices=true)

ByRows — Compare rows

false or 0 (default) | true or 1

Whether to compare the rows of A, specified as logical 0 (false) or 1 (true). Specify ByRows to find rows in A that are unique, within tolerance.

When ByRows is true:

• A must be a 2-D array.

• uniquetol compares the rows of A by considering each column separately. For two rows to be within tolerance of one another, each column has to be in tolerance.

• Each row in A is within tolerance of a row in C. However, no two rows in C are within tolerance of each other.

Two rows, u and v, are within tolerance if all(abs(u-v) <= tol*max(abs(A),[],1)).

Example: C = uniquetol(A,tol,ByRows=true)

DataScale — Scale of data

scalar | vector

Scale of data, specified as a scalar or vector. Specify DataScale as a numeric scalar, DS, to change the tolerance test to be abs(u-v) <= tol*DS.

When you specify both DataScale and ByRows, DataScale can be a vector. In this case, each element of the vector specifies DS for a corresponding column in A. If a value in the DataScale vector is Inf, then uniquetol ignores the corresponding column in A.

Example: C = uniquetol(A,DataScale=1)

Example: [C,IA,IC] = uniquetol(A,ByRows=true,DataScale=[eps(1) eps(10) eps(100)])

Data Types: single | double

PreserveRange — Preserve range

false or 0 (default) | true or 1

Whether to preserve the range of A, specified as logical 0 (false) or 1 (true). If PreserveRange is true, then the minimum and maximum values in the output C are the same as those in A.

If PreserveRange is false and the minimum and maximum values in A are within the tolerance tol of each other, then uniquetol returns only one of the values.

Example: C = uniquetol(A,tol,PreserveRange=true)

Output Arguments

C — Unique elements within tolerance

vector | matrix

Unique elements within tolerance, returned as a vector or matrix.

If A is a row vector, then C is also a row vector. Otherwise, C is a column vector. The elements in C are sorted in ascending order. Each element in A is within tolerance of an element in C, but no two elements in C are within tolerance of each other.

If ByRows is true, then C is a matrix containing the unique rows in A. In this case, the rows in C are sorted in ascending order by the first column. Each row in A is within tolerance of a row in C, but no two rows in C are within tolerance of each other.

IA — Index to A

column vector | cell array

Index to A, returned as a column vector of indices to the first occurrence of repeated elements or as a cell array. IA generally satisfies C = A(IA), with these exceptions:

• If the ByRows option is true, then C = A(IA,:).

• If OutputAllIndices is true, then IA is a cell array and C(i) and A(IA{i}) are within tolerance of each other.

IC — Index to C

column vector

Index to C, returned as a column vector of indices. IC satisfies the following properties, where ~ means the values are within tolerance of each other.

• If A is a vector, then A~C(IC).

• If A is a matrix, then A(:)~C(IC).

• If ByRows is true, then A~C(IC,:).

Algorithms

uniquetol sorts the input lexicographically, and then starts at the lowest or highest value to find unique values within tolerance. As a result, changing the sorting of the input could change the output. For example, uniquetol(-A) might not give the same results as -uniquetol(A).

There can be multiple valid C outputs that satisfy the condition, no two elements in C are within tolerance of each other. The uniquetol function can return several of the valid outputs, depending on whether the value of occurrence is "highest" or "lowest" and whether PreserveRange is specified.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• The OutputAllIndices name-value argument is not supported.

• The query array must be a vector unless the value of ByRows is true.

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Refer to the usage notes and limitations in the C/C++ Code Generation section. The same usage notes and limitations apply to GPU code generation.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

The uniquetol function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The uniquetol function supports GPU array input with these usage notes and limitations:

• The occurrence argument for occurrence of unique values is not supported.

• The ByRows, OutputAllIndices, and PreserveRange name-value arguments are not supported.

• 64-bit integers are not supported.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2015a

R2026a: Code generation support

You can generate C/C++ code for the uniquetol function.

R2021b: Options to control element selection and preserve range of data

The occurrence argument controls whether the algorithm begins with the highest or lowest elements in the input data. The PreserveRange name-value argument specifies whether the range of the output data should be the same as the input data.