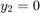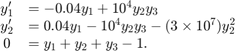ode15s
Solve stiff differential equations and DAEs — variable order method
Syntax
Description
[,
where t,y] =
ode15s(odefun,tspan,y0)tspan = [t0 tf], integrates the system of
differential equations from t0 to tf with
initial conditions y0. Each row in the solution
array y corresponds to a value returned in column
vector t.
All MATLAB® ODE solvers can solve systems of equations of
the form ,
or problems that involve a mass matrix, .
The solvers all use similar syntaxes. The ode23s solver
only can solve problems with a mass matrix if the mass matrix is constant. ode15s and ode23t can
solve problems with a mass matrix that is singular, known as differential-algebraic
equations (DAEs). Specify the mass matrix using the Mass option
of odeset.
[ additionally
finds where functions of (t,y),
called event functions, are zero. In the output, t,y,te,ye,ie]
= ode15s(odefun,tspan,y0,options)te is
the time of the event, ye is the solution at the
time of the event, and ie is the index of the triggered
event.
For each event function, specify whether the integration is
to terminate at a zero and whether the direction of the zero crossing
matters. Do this by setting the 'Events' property
to a function, such as myEventFcn or @myEventFcn,
and creating a corresponding function: [value,isterminal,direction]
= myEventFcn(t,y).
For more information, see ODE Event Location.
Examples
Input Arguments
Output Arguments
Algorithms
ode15s is a variable-step, variable-order
(VSVO) solver based on the numerical differentiation formulas (NDFs)
of orders 1 to 5. Optionally, it can use the backward differentiation
formulas (BDFs, also known as Gear's method) that are usually less
efficient. Like ode113, ode15s is
a multistep solver. Use ode15s if ode45 fails
or is very inefficient and you suspect that the problem is stiff,
or when solving a differential-algebraic equation (DAE) [1], [2].
References
[1] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.
[2] Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, “Solving Index-1 DAEs in MATLAB and Simulink,” SIAM Review, Vol. 41, 1999, pp. 538–552.
Extended Capabilities
Version History
Introduced before R2006a