Find the Length of a Pendulum in Motion
This example shows you how to calculate the length of a pendulum in motion by segmenting the pendulum and calculating the center of the pendulum across many image frames, then fitting the center coordinates to the equation of a circle.
Step 1: Load Images
Load the pendulum data from a MAT file. The file contains two variables. The frames variable contains the video as a 4-D numeric array. The rect variable contains a region of interest that bounds the extent of the pendulum.
load pendulum;
Preview the video using implay. You can see that the pendulum is swinging in the upper half of each frame.
implay(frames);

Step 2: Select Region where Pendulum is Swinging
To improve the efficiency of the segmentation, create a new series of frames that contains only the region where the pendulum is swinging.
First perform imcrop on one frame, specifyiing the cropping region as the preloaded rect variable. Next, initialize an array to store all of the cropped frames, based on the size of the first cropped frame. Finally, loop through all of the frames, crop each one using the same cropping region, and save the result to the initialized array.
first_frame = frames(:,:,:,1); first_region = imcrop(first_frame,rect); nFrames = size(frames,4); frame_regions = repmat(uint8(0), [size(first_region) nFrames]); for count = 1:nFrames frame_regions(:,:,:,count) = imcrop(frames(:,:,:,count),rect); end imshow(frame_regions(:,:,:,1))

Step 3: Segment the Pendulum in Each Frame
Notice that the pendulum is much darker than the background. You can segment the pendulum in each frame by converting the frame to grayscale, thresholding it using imbinarize, and removing background structures using imopen and imclearborder.
Initialize a binary array to contain the segmented pendulum frames.
seg_pend = false([size(first_region,1) size(first_region,2) nFrames]);
centroids = zeros(nFrames,2);
se_disk = strel("disk",3);
Loop through all of the frames and perform the segmentation and postprocessing. In a montage, display the original frame and the segmentation result.
for count = 1:nFrames fr = frame_regions(:,:,:,count); gfr = im2gray(fr); gfr = imcomplement(gfr); bw = imbinarize(gfr,0.7); % Threshold is determined experimentally bw = imopen(bw,se_disk); bw = imclearborder(bw); seg_pend(:,:,count) = bw; montage({fr,labeloverlay(gfr,bw)}); pause(0.2) end

Step 4: Find the Center of the Segmented Pendulum in Each Frame
You can see that the shape of the pendulum varied in different frames. This is not a serious issue because you just need its center. You will use the pendulum centers to find the length of the pendulum.
Use regionprops to calculate the center of the pendulum.
pend_centers = zeros(nFrames,2); for count = 1:nFrames property = regionprops(seg_pend(:,:,count),"Centroid"); pend_centers(count,:) = property.Centroid; end
Display the pendulum centers using plot.
x = pend_centers(:,1); y = pend_centers(:,2); figure plot(x,y,"m.") axis ij axis equal hold on; xlabel("x"); ylabel("y"); title("Pendulum Centers");
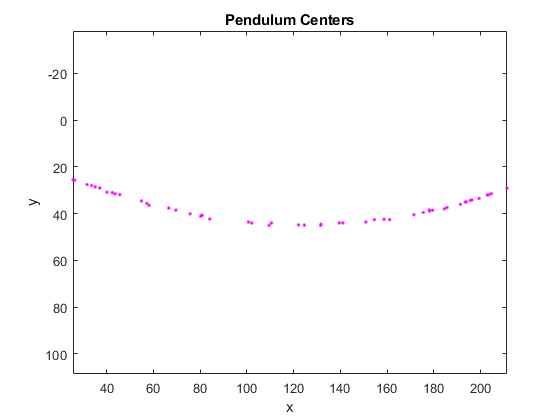
Step 5: Calculate Radius by Fitting a Circle Through Pendulum Centers
Rewrite the basic equation of a circle:
(x-xc)^2 + (y-yc)^2 = radius^2
where (xc,yc) is the center, in terms of parameters a, b, c as
x^2 + y^2 + a*x + b*y + c = 0
where a = -2*xc, b = -2*yc, and c = xc^2 + yc^2 - radius^2.
You can solve for parameters a, b, and c using the least squares method. Rewrite the above equation as
a*x + b*y + c = -(x^2 + y^2)
which can also be rewritten as
[x y 1] * [a;b;c] = -x^2 - y^2.
Solve this equation using the backslash(\) operator.
The circle radius is the length of the pendulum in pixels.
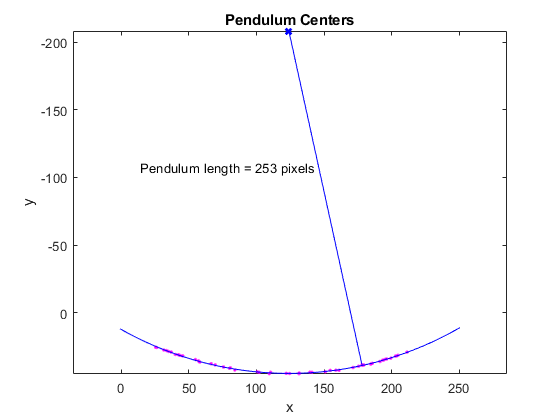
abc = [x y ones(length(x),1)] \ -(x.^2 + y.^2); a = abc(1); b = abc(2); c = abc(3); xc = -a/2; yc = -b/2; circle_radius = sqrt((xc^2 + yc^2) - c); pendulum_length = round(circle_radius)
pendulum_length = 253
Superimpose the circle and circle center on the plot of pendulum centers.
circle_theta = pi/3:0.01:pi*2/3; x_fit = circle_radius*cos(circle_theta)+xc; y_fit = circle_radius*sin(circle_theta)+yc; plot(x_fit,y_fit,"b-"); plot(xc,yc,"bx","LineWidth",2); plot([xc x(1)],[yc y(1)],"b-"); text(xc-110,yc+100,sprintf("Pendulum length = %d pixels",pendulum_length));
See Also
regionprops | imclearborder | imopen | imbinarize | imcomplement | labeloverlay
