What are Neural State-Space Models?

A neural state-space model is a type of nonlinear state-space model where you use neural networks to model the state-transition and measurement functions defining the system. You can identify the weights and biases of these networks using System Identification Toolbox™ software. You can use the trained model to simulate and predict model output at the command line, in the System Identification app, or in Simulink^®. You can also use the trained model for control, estimation, optimization, and reduced order modeling.

Structure of Neural State-Space Models

A state-space model is a representation of a dynamic system that uses a state equation and an output equation.

The state equation is a set of first-order ordinary differential equations (ODEs) or difference equations, which are often derived from first principles (white-box modeling). In practice, however, finding analytical equations that accurately describe your system is nontrivial due to the lack of prior knowledge or inherent complex nonlinear dynamics.

In these cases, data-driven modeling (grey-box or black-box modeling) can be a useful alternative. One such data-driven approach is neural state-space modeling, which represents both the state and output equations of the nonlinear system by neural networks.

Continuous-time neural state-space models have the following general form consisting of a state equation and output equation,

$\begin{array}{l} \dot{x} (t) = F (t, x (t), u (t)) \\ y (t) = [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] = [\begin{matrix} x (t) + e_{1} (t) \\ H (t, x (t), u (t)) + e_{2} (t) \end{matrix}] \end{array}$

where the state function F and the nontrivial output function H are approximated by neural networks. Here, x, u, and y are vectors representing the plant state, input, and measured output, respectively. t represents the independent variable time.

When the state is unmeasurable, to enable the training of the state function, the measured output is used as the state. So you fix the output y to be equal to the state x. If the state is measurable, you fix the state to be equal to the first part of the output, y₁, and you fix the second part, y₂, to be equal to the measured output and concatenate it with the first part to form the output y. Here, e₁ and e₂ are measurement noises in the data sets which are minimized by the network training algorithm.

For discrete-time state-space systems, the state and output equations have this form.

$\begin{array}{l} x (t + 1) = F (t, x (t), u (t)) \\ y (t) = [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] = [\begin{matrix} x (t) + e_{1} (t) \\ H (t, x (t), u (t)) + e_{2} (t) \end{matrix}] \end{array}$

where x(t+1) represents the plant state at the next sample time.

Defining and Estimating Neural State-Space Models

Estimating a neural state-space model requires the states of the system to be measured. If they are not measured, then you can treat the output as the state.

To create a black-box continuous-time or discrete-time neural state-space model with identifiable network weights and biases, use idNeuralStateSpace. You can change the default state and output network of the model by assigning a multi-layer perceptron network or a custom network as the state or output function network.

A multi-layer perceptron network (MLP) is a class of feedforward artificial neural networks (ANNs). An MLP consists of atleast three layers of nodes: an input layer, one or more hidden layers, and an output layer. A custom network refers to any neural network structure that you can create using dlnetwork (Deep Learning Toolbox).

An MLP network has a fixed structure and is simple to use. The training of this network is usually faster. On the other hand, a custom network allows advanced designs of network structures that can improve the performance. For an example, see Augment Known Linear Model with Flexible Nonlinear Functions. You also have the flexibility to use some advanced layers from Deep Learning Toolbox™ like dropoutLayer and batchNormalizationLayer when creating a custom network.

Multi-layer perceptron (MLP) networks with at least one hidden layer featuring squashing functions (such as hyperbolic tangent or sigmoid) are universal approximators, that is, are theoretically capable of approximating any function to any desired degree of accuracy provided that sufficiently many hidden units are available. Deeper networks (networks with more hidden layers) can approximate compositional functions as well as shallow networks but with exponentially lower number of training parameters and sample complexity.

To assign an MLP network as the state or output function network, use createMLPNetwork. To assign a custom network, directly assign a dlnetwork object as the state or output function or use setNetwork.

To train a neural state-space model using measured time-domain system data, use nlssest, which updates the weights and biases of the network. You can train the model using the Adam, SGDM, RMSProp, or L-BFGS solvers. For more information on these algorithms, see the Algorithms section of trainingOptions (Deep Learning Toolbox).

A new training starts with the previously trained network. To reset the network, you can either manually assign the learnables of the dlnetwork object or initialize it.

Autoencoders in Neural State-Space Models

Use autoencoders in neural state-space models to map the model states into a latent space of a different dimension compared to the original state space. Doing so enables you to project the states into a lower-dimensional space for reduced order modeling applications. You can also choose a larger latent space dimension than the original dimension, which is useful for linearizing the state transition function in the latent space.

Discrete-time state-space systems contain a state network and output network.

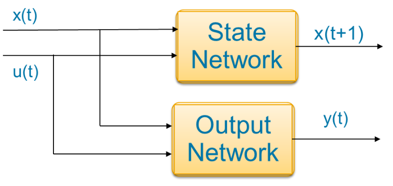
To use an autoencoder, you need to add an encoder network that transforms the input data and a decoder network that reconstructs the input data. To do so, specify the LatentDim property of the idNeuralStateSpace object as a finite positive integer.

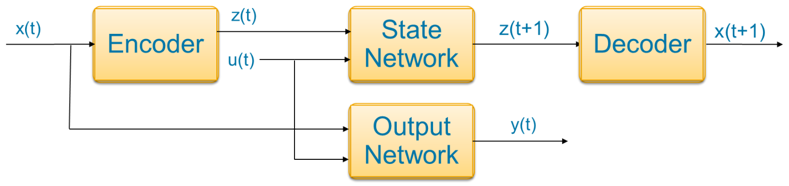
Here, x(t) is the state measurement, u(t) is the input, y(t) is the measured output, and z(t) is the latent state at time t. The four networks shown in the diagram are:

Encoder — x(t) is the input to the encoder and it usually consists of high dimensional data. The latent state z(t) is the output from the encoder. This is relatively low dimensional and captures the main characteristics of the data. The encoder maps x(t) to z(t).
State Network — z(t) and u(t) are inputs to the state network (for a time invariant system). The prediction z(t+1) is the output for discrete-time systems. You train a state network to learn a state transition function that maps z(t) to z(t+1).
Decoder — z(t+1) is the input to the decoder. x(t+1) is the output of the decoder, which is the reconstructed state. The decoder maps the latent state space back to the original state space.
Output Network — The output y(t) has two parts. The first part of the output function is y₁(t) = x(t), which implies the direct measurement of the states. For the second part, a trained output neural network maps the inputs x(t) and u(t) to the output y₂(t) (for a time invariant system). The second part of the output function only exists if the number of measured outputs is greater than the number of states.

Time-varying discrete-time neural state-space models with autoencoder have the following general form,

$\begin{array}{l} z (t) = e (x (t)) \\ z (t + 1) = f (t, z (t), u (t)) \\ x (t + 1) = d (z (t + 1)) \\ y_{1} (t) = x (t) + e_{1} (t) \\ y_{2} (t) = g (t, x (t), u (t)) + e_{2} (t) \\ y (t) = [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] \end{array}$

where e is the encoder function, f is the state function, d is the decoder function, and g is the non-trivial output function.

Similarly, time-varying continuous-time neural state-space models with autoencoder have this form.

$\begin{array}{l} z (t) = e (x (t)) \\ \dot{z} (t) = f (t, z (t), u (t)) \\ \dot{x} (t) = d (\dot{z} (t)) \\ y_{1} (t) = x (t) + e_{1} (t) \\ y_{2} (t) = g (t, x (t), u (t)) + e_{2} (t) \\ y (t) = [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] \end{array}$