Continuous-Discrete Conversion Methods
System Identification Toolbox™ offers several discretization and interpolation methods for converting identified dynamic system models between continuous time and discrete time and for resampling discrete-time models. Some methods tend to provide a better frequency-domain match between the original and converted systems, while others provide a better match in the time domain. Use the following table to help select the method that is best for your application.
| Discretization Method | Use When |
|---|---|
| Zero-Order Hold | You want an exact discretization in the time domain for staircase inputs. |
| First-Order Hold | You want an exact discretization in the time domain for piecewise linear inputs. |
| Impulse-Invariant Mapping (continuous-to-discrete conversion only) | You want an exact discretization in the time domain for impulse train inputs. |
| Tustin Approximation |
|
| Zero-Pole Matching Equivalents |
|
| Least Squares (Control System Toolbox) (continuous-to-discrete conversion only) |
|
For information about how to specify a conversion method at the command line, see
c2d, d2c, and d2d. You can experiment interactively with different discretization methods
in the Live Editor using the Convert Model
Rate (Control System Toolbox) task (requires a license).
Zero-Order Hold
The Zero-Order Hold (ZOH) method provides an exact match between the continuous- and discrete-time systems in the time domain for staircase inputs.
The following block diagram illustrates the zero-order-hold discretization Hd(z) of a continuous-time linear model H(s).
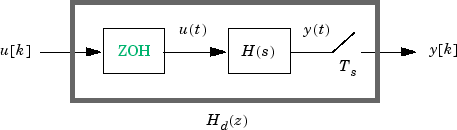
The ZOH block generates the continuous-time input signal u(t) by holding each sample value u(k) constant over one sample period:
The signal u(t) is the input to the continuous system H(s). The output y[k] results from sampling y(t) every Ts seconds.
Conversely, given a discrete system Hd(z), d2c produces a continuous system H(s). The ZOH discretization of H(s) coincides with Hd(z).
The ZOH discrete-to-continuous conversion has the following limitations:
d2ccannot convert LTI models with poles at z = 0.For discrete-time LTI models having negative real poles, ZOH
d2cconversion produces a continuous system with higher order. The model order increases because a negative real pole in the z domain maps to a pure imaginary value in the s domain. Such mapping results in a continuous-time model with complex data. To avoid this issue, the software instead introduces a conjugate pair of complex poles in the s domain.
ZOH Method for Systems with Time Delays
You can use the ZOH method to discretize SISO or MIMO continuous-time models with time delays. The ZOH method yields an exact discretization for systems with input delays, output delays, or transport delays.
For systems with internal delays (delays in feedback loops), the ZOH method results in approximate discretizations. The following figure illustrates a system with an internal delay.

For such systems, c2d performs the following actions to
compute an approximate ZOH discretization:
Decomposes the delay τ as with .
Absorbs the fractional delay into H(s).
Discretizes H(s) to H(z).
Represents the integer portion of the delay kTs as an internal discrete-time delay z–k. The final discretized model appears in the following figure:

First-Order Hold
The First-Order Hold (FOH) method provides an exact match between the continuous- and discrete-time systems in the time domain for piecewise linear inputs.
FOH differs from ZOH by the underlying hold mechanism. To turn the input samples u[k] into a continuous input u(t), FOH uses linear interpolation between samples:
In general, this method is more accurate than ZOH for systems driven by smooth inputs.
This FOH method differs from standard causal FOH and is more appropriately called triangle approximation (see [2], p. 228). The method is also known as ramp-invariant approximation.
FOH Method for Systems with Time Delays
You can use the FOH method to discretize SISO or MIMO continuous-time models with time delays. The FOH method handles time delays in the same way as the ZOH method. See ZOH Method for Systems with Time Delays.
Impulse-Invariant Mapping
The impulse-invariant mapping produces a discrete-time model with the same impulse response as the continuous time system. For example, compare the impulse response of a first-order continuous system with the impulse-invariant discretization:
G = tf(1,[1,1]);
Gd1 = c2d(G,0.01,'impulse');
impulse(G,Gd1)
The impulse response plot shows that the impulse responses of the continuous and discretized systems match.
Impulse-Invariant Mapping for Systems with Time Delays
You can use impulse-invariant mapping to discretize SISO or MIMO continuous-time
models with time delays, except that the method does not support
ss models with internal delays. For supported models,
impulse-invariant mapping yields an exact discretization of the time delay.
Tustin Approximation
The Tustin or bilinear approximation yields the best frequency-domain match between the continuous-time and discretized systems. This method relates the s-domain and z-domain transfer functions using the approximation:
In c2d conversions, the discretization Hd(z) of a continuous transfer function H(s) is:
Similarly, the d2c conversion relies on the inverse
correspondence
When you convert a state-space model using the Tustin method, the states are not preserved. The state transformation depends upon the state-space matrices and whether the system has time delays. For example, for an explicit (E = I) continuous-time model with no time delays, the state vector w[k] of the discretized model is related to the continuous-time state vector x(t) by:
Ts is the sample time of the discrete-time model. A and B are state-space matrices of the continuous-time model.
The Tustin approximation is not defined for systems with poles at z = –1 and is ill-conditioned for systems with poles near z = –1.
Tustin Approximation with Frequency Prewarping
If your system has important dynamics at a particular frequency that you want the transformation to preserve, you can use the Tustin method with frequency prewarping. This method ensures a match between the continuous- and discrete-time responses at the prewarp frequency.
The Tustin approximation with frequency prewarping uses the following transformation of variables:
This change of variable ensures the matching of the continuous- and discrete-time frequency responses at the prewarp frequency ω, because of the following correspondence:
Tustin Approximation for Systems with Time Delays
You can use the Tustin approximation to discretize SISO or MIMO continuous-time models with time delays.
By default, the Tustin method rounds any time delay to the nearest multiple of the
sample time. Therefore, for any time delay tau, the integer
portion of the delay, k*Ts, maps to a delay of
k sampling periods in the discretized model. This approach
ignores the residual fractional delay, tau
-
k*Ts.
You can approximate the fractional portion of the delay by a discrete all-pass
filter (Thiran filter) of specified order. To do so, use the
ThiranOrder option of c2dOptions.
To understand how the Tustin method handles systems with time delays, consider the following SISO state-space model G(s). The model has input delay τi, output delay τo, and internal delay τ.

The following figure shows the general result of discretizing G(s) using the Tustin method.

By default, c2d converts the time delays to pure integer time
delays. The c2d command computes the integer delays by rounding
each time delay to the nearest multiple of the sample time
Ts. Thus, in the default case, mi =
round(τi/Ts),
mo =
round(τo/Ts),
and m =
round(τ/Ts).. Also in this case,
Fi(z) =
Fo(z) =
F(z) = 1.
If you set ThiranOrder to a non-zero value,
c2d approximates the fractional portion of the time delays
by Thiran filters
Fi(z),
Fo(z), and
F(z).
The Thiran filters add additional states to the model. The maximum number of
additional states for each delay is ThiranOrder.
For example, for the input delay τi, the order of the Thiran filter Fi(z) is:
order(Fi(z))
=
max(ceil(τi/Ts),
ThiranOrder).
If
ceil(τi/Ts)
< ThiranOrder, the Thiran filter
Fi(z)
approximates the entire input delay τi. If
ceil(τi/Ts)
> ThiranOrder, the Thiran filter only approximates a portion
of the input delay. In that case, c2d represents the remainder
of the input delay as a chain of unit delays
z–mi,
where
mi =
ceil(τi/Ts)
– ThiranOrder
c2d uses Thiran filters and ThiranOrder in
a similar way to approximate the output delay
τo and the internal delay
τ.
When you discretizetf and zpk models
using the Tustin method, c2d first aggregates all input,
output, and transport delays into a single transport delay
τTOT for each channel.
c2d then approximates
τTOT as a Thiran filter and a chain of
unit delays in the same way as described for each of the time delays in
ss models.
For more information about Thiran filters, see the thiran (Control System Toolbox) reference page and [4].
Zero-Pole Matching Equivalents
This method of conversion, which computes zero-pole matching equivalents, applies only to SISO systems. The continuous and discretized systems have matching DC gains. Their poles and zeros are related by the transformation:
where:
zi is the ith pole or zero of the discrete-time system.
si is the ith pole or zero of the continuous-time system.
Ts is the sample time.
See [2] for more information.
Zero-Pole Matching for Systems with Time Delays
You can use zero-pole matching to discretize SISO continuous-time models with time
delay, except that the method does not support ss models with
internal delays. The zero-pole matching method handles time delays in the same way
as the Tustin approximation. See Tustin Approximation for Systems with Time Delays.
Least Squares
The least squares method minimizes the error between the frequency responses of the continuous-time and discrete-time systems up to the Nyquist frequency using a vector-fitting optimization approach. This method is useful when you want to capture fast system dynamics but must use a larger sample time, for example, when computational resources are limited.
This method is supported only by the c2d function and only for SISO
systems.
As with Tustin approximation and zero-pole matching, the least squares method provides a good match between the frequency responses of the original continuous-time system and the converted discrete-time system. However, when using the least squares method with:
The same sample time as Tustin approximation or zero-pole matching, you get a smaller difference between the continuous-time and discrete-time frequency responses.
A lower sample time than what you would use with Tustin approximation or zero-pole matching, you can still get a result that meets your requirements. Doing so is useful if computational resources are limited, since the slower sample time means that the processor must do less work.
References
[1] Åström, K.J. and B. Wittenmark, Computer-Controlled Systems: Theory and Design, Prentice-Hall, 1990, pp. 48-52.
[2] Franklin, G.F., Powell, D.J., and Workman, M.L., Digital Control of Dynamic Systems (3rd Edition), Prentice Hall, 1997.
[3] Smith, J.O. III, "Impulse Invariant Method", Physical Audio Signal Processing, August 2007. https://www.dsprelated.com/dspbooks/pasp/Impulse_Invariant_Method.html.
[4] T. Laakso, V. Valimaki, "Splitting the Unit Delay", IEEE Signal Processing Magazine, Vol. 13, No. 1, p.30-60, 1996.
See Also
Functions
c2d|d2c|c2dOptions|d2cOptions|d2d|d2dOptions|thiran(Control System Toolbox)
Live Editor Tasks
- Convert Model Rate (Control System Toolbox)