Fuzzy PID Controller
Libraries:
Fuzzy Logic Toolbox
Description
The Fuzzy PID Controller block implements a PID controller with a single Fuzzy Logic Controller block and parallel structure. The control architecture is shown in the following figure.
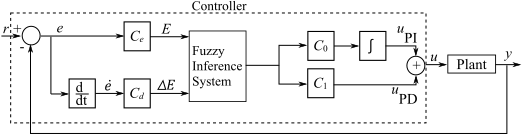
For this controller:
The inputs to the block are the reference signal (r) and the plant output (y).
The inputs to the FIS are the error (E) and the change in error (ΔE).
The error signal is scaled by gain factor Ce.
The change in error is scaled by gain factor Cd.
The FIS has a single output that splits into a PI control branch and a PD control branch.
The PI control branch contains gain C0 and an integrator.
The PD control branch contains gain C1.
The control signal output by the block is the sum of the PI and PD branches.
For more information on this controller structure, see [1].
Examples
Implement Fuzzy PID Controller in Simulink
Implement a fuzzy PID controller using a lookup table, and compare the controller performance with a traditional PID controller.
Fuzzy PID Control with Type-2 FIS
Create a type-2 fuzzy logic PID controller and compare its performance with a type-1 fuzzy PID controller and a conventional PID controller.
Fuzzy Logic Control for House Heating System
Use a fuzzy PID controller to regulate the temperature of a house, balancing the trade off between comfort and cost.
- Since R2024b
- Open Live Script
Field-Oriented Control of PMSM Using Fuzzy PI Controller
Use a fuzzy PI controller for speed control of a permanent magnet synchronous motor using field-oriented control (FOC) principles.
Ports
Input
Reference signal to track.
Output of the system under control.
Output
Controller output, based on a sum of the PI, PD, and feedforward controller paths.
Difference between the reference signal r and plant output y. Use this output for tracking error metrics, such as the integral of absolute (IAE).
Dependencies
To enable this port, select the Add error (e) output parameter.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Controller Options
Specify either a discrete-time or continuous-time controller.
When you select Discrete-time, it is recommended that you specify an explicit sample time for the block using the Sample time parameter. Selecting Discrete-time also enables the Integrator method, and Filter method parameters.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | TimeDomainType |
| Values: | "Discrete-time" (default) | "Continuous-time" |
Specify a gain factor to scale the error signal to the range of the corresponding input variable of the FIS.
For more information on selecting initial controller gains, see Derive Controller Gains from Conventional PID Gains.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | CE |
| Values: | "1" (default) | nonnegative scalar in quotes |
Specify the gain factor applied to the derivative signal before it enters the FIS.
This gain factor is also applied in the reference feedforward path when
Derivative signal is Process output
(y).
For more information on selecting initial controller gains, see Derive Controller Gains from Conventional PID Gains.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | CD |
| Values: | "1" | nonnegative scalar in quotes |
Specify the gain factor applied to the FIS output in the PI control branch.
This gain factor is also applied in the reference feedforward path when
Derivative signal is Process output
(y).
To design a PD controller, set C0 to zero.
For more information on selecting initial controller gains, see Derive Controller Gains from Conventional PID Gains.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | C0 |
| Values: | "1" | nonnegative scalar in quotes |
Specify the gain factor applied to the FIS output in the PD control path.
To design a PI controller, set C1 to zero.
For more information on selecting initial controller gains, see Derive Controller Gains from Conventional PID Gains.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | C1 |
| Values: | "1" | nonnegative scalar in quotes |
In discrete time, the integral term of the controller transfer function is Iα(z), where α(z) depends on the integrator method you specify with this parameter.
You can specify one of the following integration methods:
Forward Euler— Forward rectangular (left-hand)Backward Euler— Backward rectangular (right-hand) approximationTrapezoidal— Bilinear approximation
For more information about the filtered derivative, see the Integrator method (Simulink) parameter of the PID Controller block.
Dependencies
To enable this parameter, set the Time Domain parameter to Discrete-time.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | IntegratorMethod |
| Values: | "Forward Euler" (default) | "Backward Euler" | "Trapezoidal" |
Select this parameter to accumulate signal in the integration stage.
When you clear Use accumulator, the integration sample time for the controller is the block sample time, as specified in the Sample time parameter.
When you select Use accumulator, the integration sample time for the controller is 1. In this case, the block sample time determines when the integral output is computed but does not impact the integral output value.
When you use an accumulator, multiply C0 by the Sample time.
Dependencies
To enable this parameter, set the Time Domain parameter to Discrete-time.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | UseAccumulator |
| Values: | "off" (default) | "on" |
Compute the derivative from one of the following signals:
Error (e)—Use the error signal, which is the difference between the plant output and the reference signal, as shown in the following figure.
Process output (y)— Use the plant output directly, as shown in the following figure. When you select this option, the controller includes a feedforward path from the reference signal to the controller output.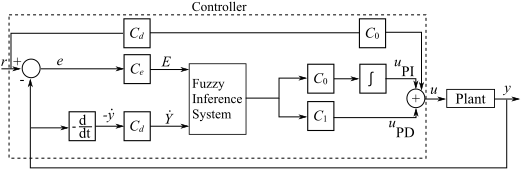
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | DerivativeSignal |
| Values: | "Error (e)" (default) | "Process output (y)" |
For discrete-time controllers, clear this option to replace the filtered derivative with an unfiltered discrete-time differentiator with pole locations that depend on the Filter method parameter.
For continuous-time controllers, the derivative term is always filtered.
For more information about the filtered derivative, see the Use filtered derivative (Simulink) parameter of the PID Controller block.
Dependencies
To enable this parameter, set Time domain to Discrete-time.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | UseFilter |
| Values: | "on" (default) | "off" |
Specify a finite, real gain value for the filter coefficient. The filter coefficient determines the pole location of the filter in the derivative action of the block. The location of the filter pole depends on the Time domain parameter.
For more information about the filter coefficient and its impact on pole locations, see the Filter coefficient (N) (Simulink) parameter of the PID Controller block.
Dependencies
To enable this parameter for discrete-time controllers, select the Use filtered derivative parameter.
This parameter is always enabled for continuous-time controllers.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | N |
| Values: | "100" (default) | positive scalar in quotes |
You can specify one of the following filter methods for the derivative term of the controller:
Forward Euler— Forward rectangular (left-hand)Backward Euler— Backward rectangular (right-hand) approximationTrapezoidal— Bilinear approximation
For more information about these methods, see the Filter method (Simulink) parameter of the PID Controller block.
Dependencies
To enable this parameter, set the Time Domain parameter to Discrete-time and select the Use filtered derivative parameter.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | DerivativeFilterMethod |
| Values: | "Forward Euler" (default) | "Backward Euler" | "Trapezoidal" |
Enable e output port for accessing the error signal.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | E |
| Values: | "off" (default) | "on" |
Specify a sample time by entering a positive scalar value, such as 0.1. The default discrete sample time of –1 means that the block inherits its sample time from upstream blocks. However, it is recommended that you set the controller sample time explicitly, especially if you expect the sample time of upstream blocks to change. The effect of the controller coefficients depend on the sample time. Thus, for a given set of coefficient values, changing the sample time changes the performance of the controller.
Dependencies
To enable this parameter, set the Time Domain parameter to Discrete-time.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | SampleTime |
| Values: | "-1" (default) | positive scalar in quotes |
Fuzzy Inference System
Fuzzy inference system, specified as one of the following:
mamfisorsugfisobject — Specify the name of a type-1 FIS object in the MATLAB® workspace.mamfistype2orsugfistype2object — Specify the name of a type-2 FIS object in the MATLAB workspace.Name of a FIS file (
*.fis) in the current working folder or on the MATLAB path. Including the file extension in the file name is optional. Specify the filename in quotes.Name of a MAT file (
*.mat) in the current working folder or on the MATLAB path. The MAT file must contain only one FIS object. Including the file extension in the file name is optional. Specify the filename in quotes.
The FIS must have two input variables (error signal and derivative signal) and one output variable.
The default FIS, fuzzycontroller, is a linear FIS configured to
allow easier selection of fuzzy PID controller gains based on specified conventional
PID controller gains. For more information about this FIS, see Default FIS.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | FIS |
| Values: | '"fuzzycontroller"' (default) | variable name in quotes | file name in quotes |
Number of samples for discretizing the range of FIS output variables, specified as an integer greater than 1. This value corresponds to the number of points in the output fuzzy set for each rule.
To reduce memory usage while evaluating Mamdani FISs, specify a lower number of samples. Doing so sacrifices the accuracy of the defuzzified output value. Specifying a low number of samples can make the output area for defuzzification zero. In this case, the defuzzified output value is the midpoint of the output variable range.
Note
The block ignores this parameter when evaluating Sugeno FISs.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | OutputSampleNumber |
| Values: | "101" (default) | integer greater than 1 in quotes |
To reduce the processing time for the controller, you can represent your FIS as a lookup table.
The block divides the input range of each FIS input into equally sized regions based on the number of breakpoints, which you specify using the Number of input breakpoints parameter.
For each input combination, the block calculates a corresponding FIS output. During evaluation, the controller uses these precomputed outputs instead of performing the fuzzy inference process.
Programmatic Use
To set the block parameter value
programmatically, use the set_param (Simulink) function.
| Parameter: | UseLookupTable |
| Values: | "off" (default) | "on" |
Number of lookup table breakpoints, specified as a positive integer. Increasing the number of breakpoints improves the accuracy of the lookup table while increasing its memory requirements.
Dependencies
To enable this parameter, select the Implement FIS as lookup table parameter.
Programmatic Use
To set the block parameter value
programmatically, use the set_param (Simulink) function.
| Parameter: | NumBreakpoints |
| Values: | "10" (default) | positive integer in quotes |
Algorithms
The default fuzzycontroller FIS for the Fuzzy PID Controller block is
a Sugeno FIS with a linear control surface. This default FIS configuration is proposed in
[2].
![Linear control surface with error and rate input variables, both with range [-1,1] and output variable with range [-2,2].](fuzzy-pid-control-surface.png)
The linear control surface allows you to compute controller gains based on conventional PID gains. To simplify controller gain calculations, the output variable range of the FIS is double the range of each input variable. For more information, see Derive Controller Gains from Conventional PID Gains.
Each input variable has two triangular membership functions, positive
and negative,
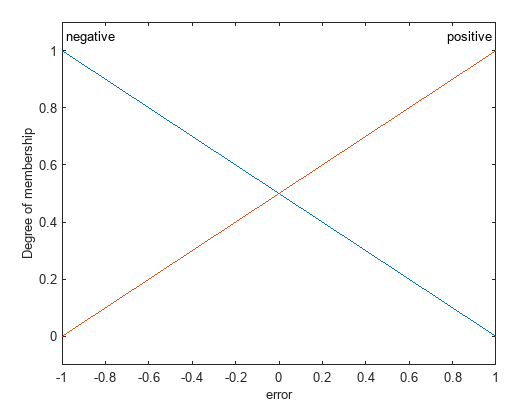
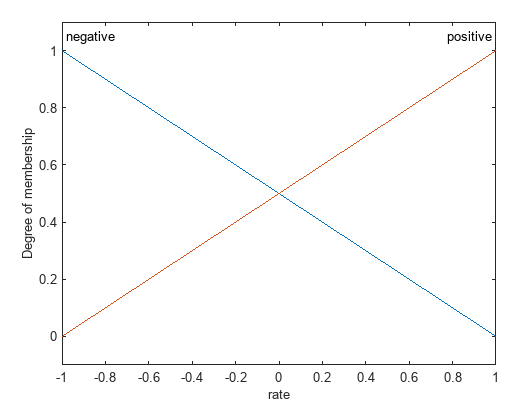
The output variable has three constant membership functions located at –1, 0, and 1
named negative, zero, and positive,
respectively.
To generate a linear control surface using these membership functions,
fuzzycontroller uses the following rules:
If (error is negative) and (rate is negative) then (u is negative)If (error is positive) and (rate is negative) then (u is zero)If (error is negative) and (rate is positive) then (u is zero)If (error is positive) and (rate is positive) then (u is positive)
You can use the following approach to design your fuzzy PID controller based on the tuned gain values from a conventional PID controller.
Design a conventional PID controller and obtain gain values Kp, Ki, and Kd.
Determine the expected ranges of the FIS inputs and outputs for your application, where [–L,L] is the range for both input variables and [–H,H] is the range for the output variable.
Select initial values for the Ce, Cd, C0, and C1 gain parameters based on the conventional PID gains and signal ranges.
Design a nonlinear control surface by modifying the rule base of your FIS.
For an example that uses this approach, see Implement Fuzzy PID Controller in Simulink.
If you assume a linear control surface for your FIS, the fuzzy PID controller gains are related to the conventional PID gains as follows:
You can select Ce based on the expected error and FIS input error range. For example, if the input range for the error signal is [–1,1] and the maximum expected error magnitude is 10, set Ce to 0.1.
You can then solve for Cd, C0, and C1.
You can simplify your gain calculations by setting the FIS variable ranges such that H = 2L.
References
[1] Xu, J. X., Hang, C. C., Liu, C. "Parallel structure and tuning of a fuzzy PID controller." Automatica, Vol. 36, pp. 673-684. 2000.
[2] Ying, Hao. Fuzzy Control and Modeling: Analytical Foundations and Applications. IEEE Press Series in Biomedical Engineering. New York: IEEE Press, 2000.
Extended Capabilities
Usage notes and limitations:
Continuous-time controller:
Not recommended for production code.
Discrete-time controller:
Depends on absolute time when placed inside a triggered subsystem hierarchy.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2024b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)



