Implement Fuzzy PID Controller in Simulink
This example shows how to implement a fuzzy inference system (FIS) for nonlinear PID control and how to convert that FIS to a lookup table.
A fuzzy inference system (FIS) maps given inputs to outputs using fuzzy logic. For control applications, typical FIS inputs are the error and change of error. The FIS output is the control action inferred from the fuzzy rules. Fuzzy Logic Toolbox™ provides commands and apps for designing a FIS for a desired control surface. You can then simulate the designed FIS using the Fuzzy PID Controller block in Simulink®.
You can often approximate nonlinear control surfaces using lookup tables to simplify the generated code and improve execution speed. The Fuzzy PID Controller block allows you to implement its FIS as a 2-D lookup table.
For this example, you design a nonlinear fuzzy PID controller for a plant in Simulink. The plant is a discrete-time, single-input, single-output system. The design goal is to achieve good reference tracking performance.
Ts = 0.1; Plant = c2d(zpk([],[-1 -3 -5],1),Ts);
Fuzzy PID Controller Structure
The fuzzy controller in this example is in the feedback loop and computes PID-like actions using fuzzy inference. Open the Simulink model.
open_system("sllookuptable")
This model simulates three different controllers, each controlling the same plant.
Conventional PID controller
Fuzzy PID controller
Fuzzy PID controller implemented as a lookup table
Both fuzzy controllers are implemented using a Fuzzy PID Controller block. This controller uses a parallel structure as shown in the following figure. The controller includes PI and PD control branches following a Fuzzy Logic Controller, where the PI branch includes an integrator. For more information, see [1].

The fuzzy PID controller uses the change of the output -(y(k)-y(k-1)), instead of change of error e(k)-e(k-1), as the second input signal to the FIS. Doing so prevents the step change in reference signal from directly triggering the derivative action. The two gain blocks, Cd and C0, in the feedforward path from r to u, ensure that the error signal e is used in the proportional action when the fuzzy PID controller is linear.
Design Conventional PID Controller
The conventional PID controller in this example is a discrete-time PID controller with Backward Euler numerical integration in both the integral and derivative actions. The controller gains are Kp, Ki, and Kd.
open_system("sllookuptable/Conventional PID")
Similar to the fuzzy PID controller, the input signal to the derivative action is -y(k), instead of e(k).
You can tune the PID controller gains manually or using tuning formulas. In this example, obtain the initial PID design using the pidtune command from Control System Toolbox™.
Define the PID structure, tune the controller, and extract the PID gains.
convPID = pid(1,1,1,... Ts=Ts, ... IFormula="BackwardEuler", ... DFormula="BackwardEuler"); convPID = pidtune(Plant,convPID)
convPID =
Ts*z z-1
Kp + Ki * ------ + Kd * ------
z-1 Ts*z
with Kp = 30.6, Ki = 25.2, Kd = 9.02, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time PID controller in parallel form.
Model Properties
[Kp,Ki,Kd] = piddata(convPID);
Design Equivalent Linear Fuzzy PID Controller
By configuring the FIS and selecting the appropriate scaling factors, you can obtain a linear fuzzy PID controller that reproduces the control performance of the conventional PID controller.
First, configure the fuzzy inference system so that it produces a linear control surface from inputs E and Ydot to output u. The FIS settings are based on design choices described in [2]:
Use a Sugeno style fuzzy inference system with default inference methods.
Normalize the ranges of both inputs to [-10, 10].
Use triangular input membership functions that overlap their neighbor functions at a membership value of 0.5.
Use an output range of [-20, 20].
Use constant output membership functions.
Construct the fuzzy inference system.
FIS = sugfis;
Define input variable E.
FIS = addInput(FIS,[-10 10],Name="E"); FIS = addMF(FIS,"E","trimf",[-20 -10 0],Name="Negative"); FIS = addMF(FIS,"E","trimf",[-10 0 10],Name="Zero"); FIS = addMF(FIS,"E","trimf",[0 10 20],Name="Positive");
Define input variable Ydot.
FIS = addInput(FIS,[-10 10],Name="Ydot"); FIS = addMF(FIS,"Ydot","trimf",[-20 -10 0],Name="Negative"); FIS = addMF(FIS,"Ydot","trimf",[-10 0 10],Name="Zero"); FIS = addMF(FIS,"Ydot","trimf",[0 10 20],Name="Positive");
Define output variable u with constant membership functions.
FIS = addOutput(FIS,[-20 20],Name="u"); FIS = addMF(FIS,"u","constant",-20,Name="LargeNegative"); FIS = addMF(FIS,"u","constant",-10,Name="SmallNegative"); FIS = addMF(FIS,"u","constant",0,Name="Zero"); FIS = addMF(FIS,"u","constant",10,Name="SmallPositive"); FIS = addMF(FIS,"u","constant",20,Name="LargePositive");
Define the following fuzzy rules:
If
EisNegativeandYdotisNegative, thenuisLargeNegative.If
EisNegativeandYdotisZero, thenuisSmallNegative.If
EisNegativeandYdotisPositive, thenuisZero.If
EisZeroandYdotisNegative, thenuisSmallNegative.If
EisZeroandYdotisZero, thenuisZero.If
EisZeroandYdotisPositive, thenuisSmallPositive.If
EisPositiveandYdotisNegative, thenuisZero.If
EisPositiveandYdotisZero, thenuisSmallPositive.If
EisPositiveandYdotisPositive, thenuisLargePositive.
ruleList = [1 1 1 1 1; % Rule 1 1 2 2 1 1; % Rule 2 1 3 3 1 1; % Rule 3 2 1 2 1 1; % Rule 4 2 2 3 1 1; % Rule 5 2 3 4 1 1; % Rule 6 3 1 3 1 1; % Rule 7 3 2 4 1 1; % Rule 8 3 3 5 1 1]; % Rule 9 FIS = addRule(FIS,ruleList);
Plot the linear control surface.
gensurf(FIS)

Determine scaling factors Ce, Cd, C0, and C1 from the Kp, Ki, and Kd gains of by the conventional PID controller. Comparing the expressions of the traditional PID controller and the linear fuzzy PID controller, the variables are related as follows:
Kp= C0 * |Cd| + C1 * |Ce|Ki= C0 * |Ce|Kd= C1 * |Cd|
Assume that the maximum reference step is 1, and thus the maximum error e is 1. Since the input range of E is [-10 10], set Ce to 10. You can then solve for Cd, C0, and C1.
Ce = 10; Cd = Ce*(Kp-sqrt(Kp^2-4*Ki*Kd))/2/Ki; C0 = Ki/Ce; C1 = Kd/Cd;
Implement Fuzzy Inference System Using 2-D Lookup Table
The FIS used in the Fuzzy PID Controller block has two inputs (E and Ydot) and one output (u). Therefore, you can replace the fuzzy system using a 2-D lookup table.
The Fuzzy PID Controller block allows you to implement your FIS as a lookup table. To do so:
Select the Implement FIS as lookup table parameter.
Specify the table resolution using the Number of input breakpoints parameter.
In the sllookuptable model, the Fuzzy PID - Lookup block is configured as a lookup table with 20 breakpoints.
Simulate Closed-Loop Response in Simulink
Run the simulation. To compare the closed-loop responses to a step reference change, open the scope. As expected, all three controllers produce the same result.
sim("sllookuptable") open_system("sllookuptable/Scope")

Design Fuzzy PID Controller with Nonlinear Control Surface
Once you have a linear fuzzy PID controller, you can obtain a nonlinear control surface by adjusting your FIS settings, such as its style, membership functions, and rule base.
For this example, design a steep control surface using a Sugeno-type FIS. Each input set has two terms (Positive and Negative), and the number of rules is reduced to four.
Construct the FIS.
FIS = sugfis;
Define input E.
FIS = addInput(FIS,[-10 10],Name="E"); FIS = addMF(FIS,"E","gaussmf",[7 -10],Name="Negative"); FIS = addMF(FIS,"E","gaussmf",[7 10],Name="Positive");
Define input Ydot.
FIS = addInput(FIS,[-10 10],Name="Ydot"); FIS = addMF(FIS,"Ydot","gaussmf",[7 -10],Name="Negative"); FIS = addMF(FIS,"Ydot","gaussmf",[7 10],Name="Positive");
Define output u.
FIS = addOutput(FIS,[-20 20],Name="u"); FIS = addMF(FIS,"u","constant",-20,Name="Min"); FIS = addMF(FIS,"u","constant",0,Name="Zero"); FIS = addMF(FIS,"u","constant",20,Name="Max");
Define the following rules:
If
EisNegativeandYdotisNegative, thenuisMin.If
EisNegativeandYdotisPositive, thenuisZero.If
EisPositiveandYdotisNegative, thenuisZero.If
EisPositiveandYdotisPositive, thenuisMax.
ruleList = [1 1 1 1 1;... % Rule 1 1 2 2 1 1;... % Rule 2 2 1 2 1 1;... % Rule 3 2 2 3 1 1]; % Rule 4 FIS = addRule(FIS,ruleList);
View the nonlinear control surface. This surface has a higher gain near the center of the E and Ydot plane than the linear surface has, which helps reduce the error more quickly when the error is small. When the error is large, the controller becomes less aggressive to avoid possible saturation.
gensurf(FIS)

Run the simulation.
sim("sllookuptable")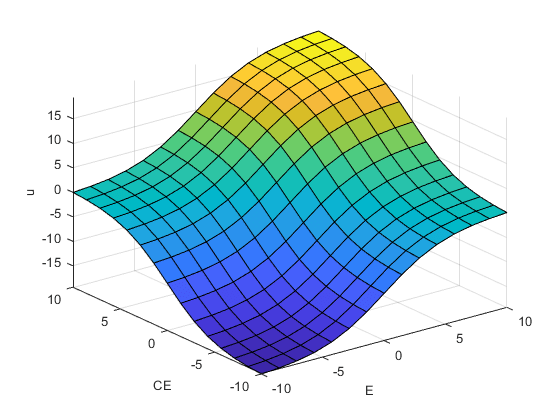
Compared with the traditional linear PID controller (the response curve with large overshoot), the nonlinear fuzzy PID controller reduces the overshoot by 50%. The two response curves from the nonlinear fuzzy controllers almost overlap, which indicates that the 2-D lookup table approximates the fuzzy system well.
References
[1] Xu, J. X., Hang, C. C., Liu, C. "Parallel structure and tuning of a fuzzy PID controller." Automatica, Vol. 36, pp. 673-684. 2000.
[2] Jantzen, J. Tuning of Fuzzy PID Controllers, Technical Report, Dept. of Automation, Technical University of Denmark. 1999.