Fuzzy Inference Process
Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic. The mapping then provides a basis from which decisions can be made, or patterns discerned. The process of fuzzy inference involves all the pieces that are described in Membership Functions, Logical Operations, and If-Then Rules.
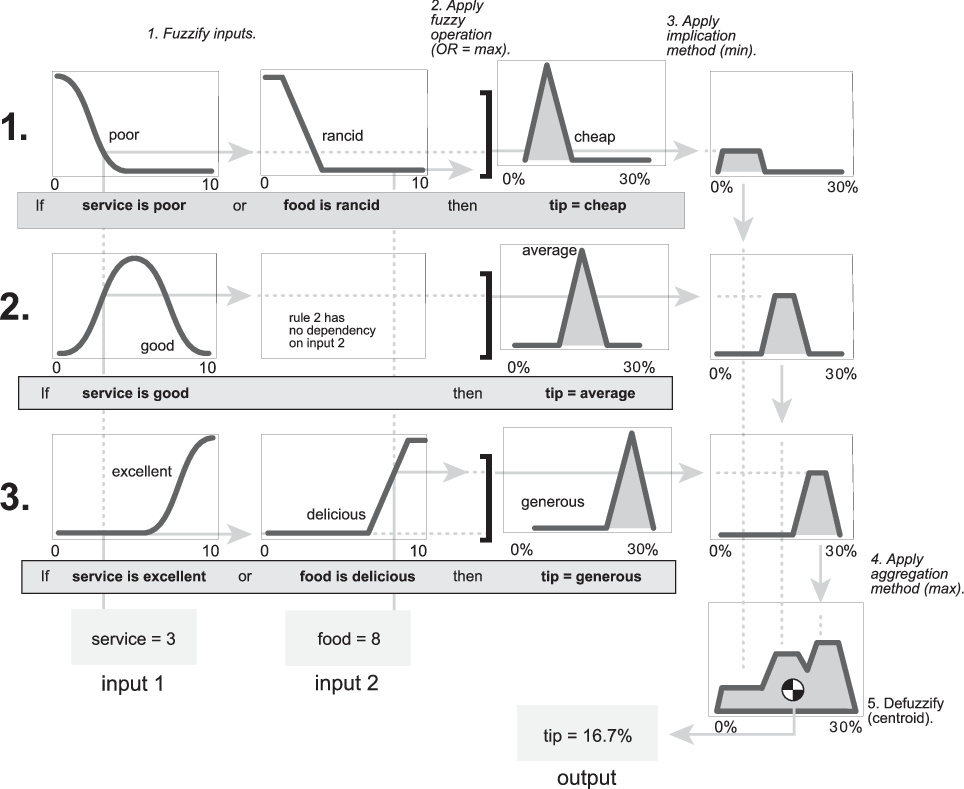
This section describes the fuzzy inference process and uses the example of the two-input, one-output, three-rule tipping problem from Fuzzy vs. Nonfuzzy Logic. The fuzzy inference system for this problem takes service and food quality as inputs and computes a tip percentage using the following rules.
If the service is poor or the food is rancid, then tip is cheap.
If the service is good, then tip is average.
If the service is excellent or the food is delicious, then tip is generous.

The parallel nature of the rules is an important aspect of fuzzy logic systems. Instead of sharp switching between modes based on breakpoints, logic flows smoothly from regions where one rule or another dominates.
The fuzzy inference process has the following steps.
Fuzzify Inputs
The first step is to take the inputs and determine the degree to which they belong to each of the appropriate fuzzy sets via membership functions (fuzzification). In Fuzzy Logic Toolbox™ software, the input is always a crisp numerical value limited to the universe of discourse of the input variable (in this case, the interval from 0 through 10). The output is a fuzzy degree of membership in the qualifying linguistic set (always the interval from 0 through 1). Fuzzification of the input amounts to either a table lookup or a function evaluation.
This example is built on three rules, and each of the rules depends on resolving the inputs into several different fuzzy linguistic sets: service is poor, service is good, food is rancid, food is delicious, and so on. Before the rules can be evaluated, the inputs must be fuzzified according to each of these linguistic sets. For example, to what extent is the food delicious? The following figure shows how well the food at the hypothetical restaurant (rated on a scale from 0 through 10) qualifies as the linguistic variable delicious using a membership function. In this case, we rate the food as an 8, which, given the graphical definition of delicious, corresponds to µ = 0.7 for the delicious membership function.

In this manner, each input is fuzzified over all the qualifying membership functions required by the rules.
Apply Fuzzy Operator
After the inputs are fuzzified, you know the degree to which each part of the antecedent is satisfied for each rule. If the antecedent of a rule has more than one part, the fuzzy operator is applied to obtain one number that represents the result of the rule antecedent. This number is then applied to the output function. The input to the fuzzy operator is two or more membership values from fuzzified input variables. The output is a single truth value.
As described in Logical Operations, any number of well-defined methods can fill in for the AND operation or the OR operation. In the toolbox, two built-in AND methods are supported: min (minimum) and prod (product). Two built-in OR methods are also supported: max (maximum) and probor (probabilistic OR). The probabilistic OR method (also known as the algebraic sum) is calculated according to the equation:
| probor(a,b) = a + b - ab |
In addition to these built-in methods, you can create your own methods for AND and OR by writing any function and setting that to be your method of choice. For more information, see Build Fuzzy Systems Using Custom Functions.
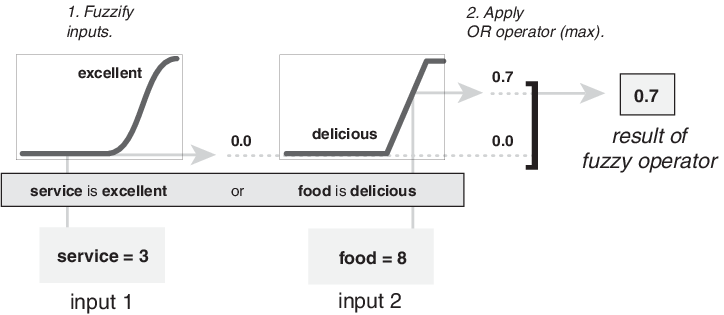
The following figure demonstrates the OR operator max by evaluating the antecedent of the third rule of the tipping calculation. For the given service and food ratings, the two elements of the antecedent (service is excellent and food is delicious) produce the fuzzy membership values 0.0 and 0.7, respectively. The fuzzy OR operator selects the maximum of the two values, 0.7. The probabilistic OR method would still result in 0.7.
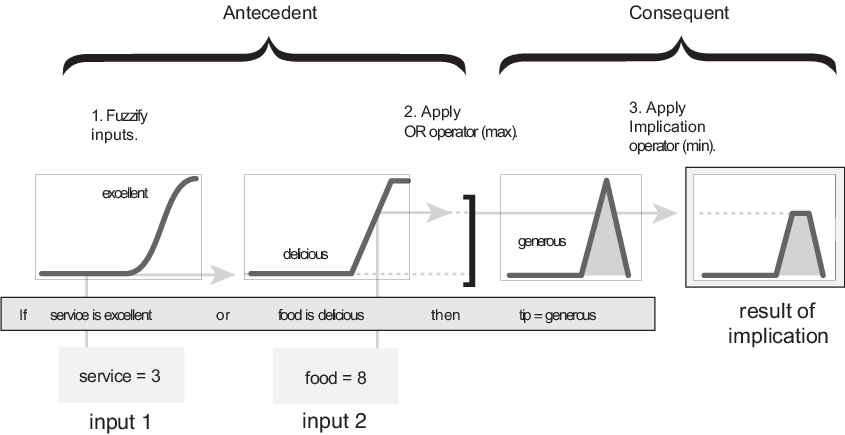
Apply Implication Method
Before applying the implication method, you must determine the rule weight. Every rule has a weight (a number from 0 through 1), which is applied to the number given by the antecedent. Generally, this weight is 1 (as it is for this example) and thus has no effect on the implication process. However, you can decrease the effect of one rule relative to the others by changing its weight value to something other than 1.
After proper weighting has been assigned to each rule, the implication method is implemented. A consequent is a fuzzy set represented by a membership function, which weights appropriately the linguistic characteristics that are attributed to it. The consequent is reshaped using a function associated with the antecedent (a single number). The input for the implication process is a single number given by the antecedent, and the output is a fuzzy set. Implication is implemented for each rule. Two built-in methods are supported, and they are the same functions that are used by the AND method: min (minimum), which truncates the output fuzzy set, and prod (product), which scales the output fuzzy set.
Note
Sugeno systems always use the product implication method.
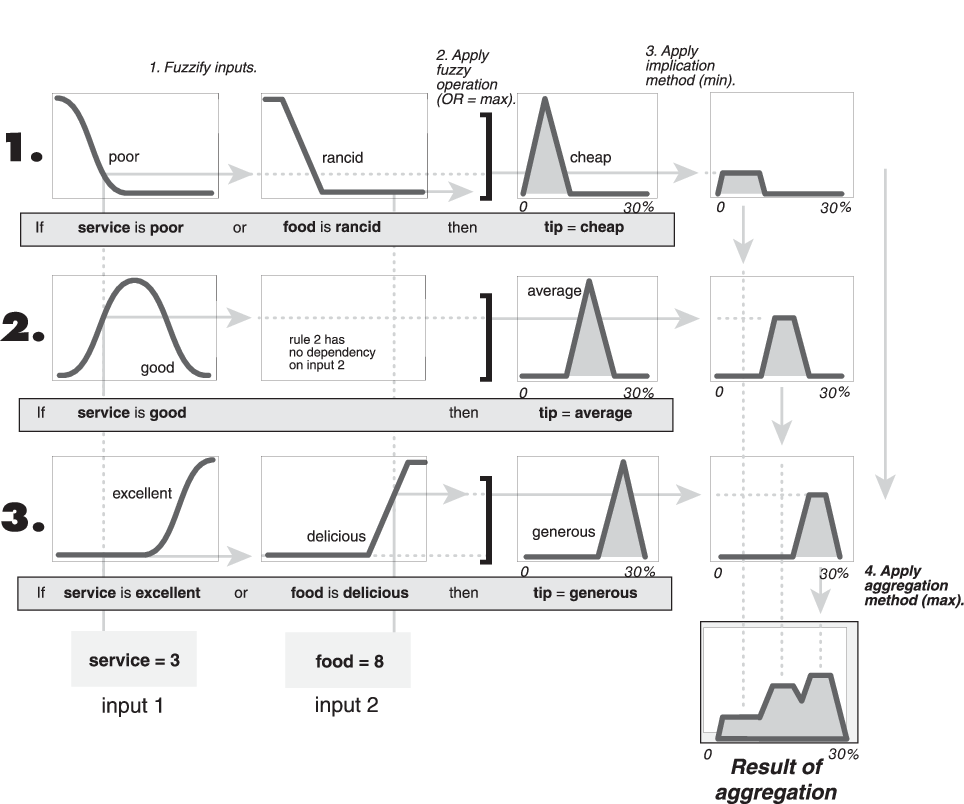
Aggregate All Outputs
Since decisions are based on testing all the rules in a FIS, the rule outputs must be combined in some manner. Aggregation is the process by which the fuzzy sets that represent the outputs of each rule are combined into a single fuzzy set. Aggregation only occurs once for each output variable, which is before the final defuzzification step. The input of the aggregation process is the list of truncated output functions returned by the implication process for each rule. The output of the aggregation process is one fuzzy set for each output variable.
As long as the aggregation method is commutative, then the order in which the rules are executed is unimportant. Three built-in methods are supported.
max(maximum)probor(probabilistic OR)sum(sum of the rule output sets)
In the following diagram, all three rules are displayed to show how the rule outputs are aggregated into a single fuzzy set whose membership function assigns a weighting for every output (tip) value.
Note
Sugeno systems always use the sum aggregation
method.
Defuzzify
The input for the defuzzification process is the aggregate output fuzzy set and the output is a single number. As much as fuzziness helps the rule evaluation during the intermediate steps, the final desired output for each variable is generally a single number. However, the aggregate of a fuzzy set encompasses a range of output values, and so must be defuzzified to obtain a single output value from the set.
There are five built-in defuzzification methods supported: centroid, bisector, middle of maximum (the average of the maximum value of the output set), largest of maximum, and smallest of maximum. Perhaps the most popular defuzzification method is the centroid calculation, which returns the center of the area under the aggregate fuzzy set, as shown in the following figure.

While the aggregate output fuzzy set covers a range from 0% though 30%, the
defuzzified value is between 5% and 25%. These limits correspond to the centroids of
the cheap and generous membership functions,
respectively.
Fuzzy Inference Diagram
The fuzzy inference diagram is the composite of all the smaller diagrams presented so far in this section. It simultaneously displays all parts of the fuzzy inference process you have examined. Information flows through the fuzzy inference diagram as shown in the following figure.
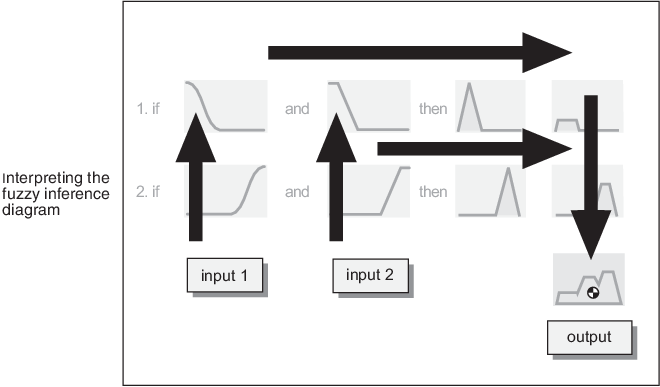
In this figure, the flow proceeds up from the inputs in the lower left, across each row, and then down the rule outputs to the lower right. This compact flow shows everything at once, from linguistic variable fuzzification all the way through defuzzification of the aggregate output.
The following figure shows the actual full-size fuzzy inference diagram for the basic tipping problem. Using a fuzzy inference diagram, you can learn a lot about how the system operates. For instance, for the particular inputs in this diagram, you can see that the implication method is truncation with the min function. The max function is used for the fuzzy OR operation. Rule 3 (the bottom-most row in the diagram shown previously) has the strongest influence on the output. For more information on viewing the rule inference diagram for a fuzzy system, see Analyze Fuzzy System Using Fuzzy Logic Designer.