rcsSignature
Radar cross-section pattern
Description
rcsSignature creates a radar cross-section (RCS) signature object.
You can use this object to model an angle-dependent and frequency-dependent radar
cross-section pattern. The radar cross-section determines the intensity of reflected radar
signal power from a target. The object models both polarized and non-polarized signals. The
object support several Swerling fluctuation models.
Creation
Description
rcssig = rcsSignaturercsSignature object with default property values.
rcssig = rcsSignature(Name,Value)Name,Value pair arguments.
Name is a property name and Value is the
corresponding value. Name must appear inside single quotes
(''). You can specify several name-value pair arguments in any order
as Name1,Value1,...,NameN,ValueN. Any unspecified properties take
default values.
Note
You can only set property values of rcsSignature when constructing the
object. The property values are not changeable after construction.
Properties
To enable polarization, set this property to true. Set this
property to false to ignore polarization.
Data Types: logical
Polarization scattering matrix form, specified as 'Full' or
'Symmetric'.
'Full'makes no assumptions about the cross-polarization terms and the polarization matrix components must all be specified (ShhPattern,SvvPattern,ShvPattern,SvhPattern). When this input method is selected, theShvPatternandSvhPatternproperties are applicable.'Symmetric'assumes reciprocity (monostatic geometry) and that the cross-polarization terms are equal (ShvPattern=SvhPattern). When this input method is selected, theShvPatternproperty is available. TheSvhPatternproperty is not available and is assumed to be equal to theShvPatternproperty.
Dependencies
To enable this property, set the EnablePolarization property
to true.
Sampled radar cross-section (RCS) pattern, specified as a scalar, a Q-by-P real-valued matrix, or a Q-by-P-by-K real-valued array. The pattern is an array of RCS values defined on a grid of elevation angles, azimuth angles, and frequencies. Azimuth and elevation are defined in the body frame of the target.
Q is the number of RCS samples in elevation.
P is the number of RCS samples in azimuth.
K is the number of RCS samples in frequency.
. Units are in dBsm.
Q, P, and K usually match
the length of the vectors defined in the Elevation,
Azimuth, and Frequency properties,
respectively, with these exceptions:
To model an RCS pattern for an elevation cut (constant azimuth), you can specify the RCS pattern as a Q-by-1 vector or a 1-by-Q-by-K matrix. Then, the azimuth vector specified in the
Azimuthproperty must have length 2.To model an RCS pattern for an azimuth cut (constant elevation), you can specify the RCS pattern as a 1-by-P vector or a 1-by-P-by-K matrix. Then, the elevation vector specified in the
Elevationproperty must have length 2.To model an RCS pattern for one frequency, you can specify the RCS pattern as a Q-by-P matrix. Then, the frequency vector specified in the
Frequencyproperty must have length 2.
Example: [10,0;0,-5]
Dependencies
To enable this property, set the EnablePolarization property
to false.
Data Types: double
Polarization scattering matrix co-polarized HH component, where
HH represents horizontal transmission and horizontal reception.
Q is the length of the vector in the Elevation
property. P is the length of the vector in the
Azimuth property. If the pattern is three-dimensional, then
K is the length of the vector in the Frequency
property.
When defining patterns for azimuth or elevation only cuts, P or
Q can equal 1, but the corresponding Azimuth
or Elevation property must still be a 2-element vector. In this
case, the Azimuth or Elevation property
defines the view angles over which the pattern is considered valid for the pattern's
dimension with length 1.
Units are in meters.
Dependencies
To enable this property, set the EnablePolarization property
to true.
Data Types: double
Complex Number Support: Yes
Polarization scattering matrix co-polarized VV component, where
VV represents vertical transmission and vertical reception.
Q is the length of the vector in the Elevation
property. P is the length of the vector in the
Azimuth property. If the pattern is three-dimensional, then
K is the length of the vector in the Frequency
property.
When defining patterns for azimuth or elevation only cuts, P or
Q can equal 1, but the corresponding Azimuth
or Elevation property must still be a 2-element vector. In this
case, the Azimuth or Elevation property
defines the view angles over which the pattern is considered valid for the pattern's
dimension with length 1.
Units are in meters.
Dependencies
To enable this property, set the EnablePolarization property
to true.
Data Types: double
Complex Number Support: Yes
Polarization scattering matrix co-polarized HV component, where
HV represents horizontal transmission and vertical reception.
Q is the length of the vector in the Elevation
property. P is the length of the vector in the
Azimuth property. If the pattern is three-dimensional, then
K is the length of the vector in the Frequency
property.
When defining patterns for azimuth or elevation only cuts, P or
Q can equal 1, but the corresponding Azimuth
or Elevation property must still be a 2-element vector. In this
case, the Azimuth or Elevation property
defines the view angles over which the pattern is considered valid for the pattern's
dimension with length 1.
Units are in meters.
Dependencies
To enable this property, set the EnablePolarization property
to true.
Data Types: double
Complex Number Support: Yes
Polarization scattering matrix co-polarized HV component, where
VH represents vertical transmission and horizontal reception.
Q is the length of the vector in the Elevation
property. P is the length of the vector in the
Azimuth property. If the pattern is three-dimensional, then
K is the length of the vector in the Frequency
property.
When defining patterns for azimuth or elevation only cuts, P or
Q can equal 1, but the corresponding Azimuth
or Elevation property must still be a 2-element vector. In this
case, the Azimuth or Elevation property
defines the view angles over which the pattern is considered valid for the pattern's
dimension with length 1.
Units are in meters.
Dependencies
To enable this property, set the EnablePolarization property
to true and set the CrossPolarization property
to 'Full'.
Data Types: double
Complex Number Support: Yes
Azimuth angles used to define the angular coordinates of each column of the matrix
or array, specified by the Pattern property. Specify the azimuth
angles as a length-P vector. P must be greater
than two. Angle units are in degrees.
When the Pattern property defines an elevation cut,
Azimuth must be a 2-element vector defining the minimum and
maximum azimuth view angles over which the elevation cut is considered valid.
Example: [-45:0.5:45]
Data Types: double
Elevation angles used to define the coordinates of each row of the matrix or array,
specified by the Pattern property. Specify the elevation angles as
a length-Q vector. Q must be greater than two.
Angle units are in degrees.
When the Pattern property defines an azimuth cut,
Elevation must be a 2-element vector defining the minimum and
maximum elevation view angles over which the azimuth cut is considered valid.
Example: [-30:0.5:30]
Data Types: double
Frequencies used to define the applicable RCS for each page of the
Pattern property, specified as a K-element
vector of positive scalars. K is the number of RCS samples in
frequency. K must be no less than two. Frequency units are in
hertz.
When the Pattern property is a matrix,
Frequency must be a 2-element vector defining the minimum and
maximum frequencies over which the pattern values are considered valid.
Example: [0:0.1:30]
Data Types: double
Fluctuation models, specified as 'Swerling0',
'Swerling1' or 'Swerling3'. Swerling cases 2 and
4 are not modeled because they are determined from how the target is sampled and are not
an inherent target property.
| Model | Description |
|---|---|
'Swerling0' | The target RCS is assumed to be non-fluctuating. In this case the instantaneous RCS signature value retrieved by the value method is deterministic. This model represents ideal radar targets with an RCS that remains constant in time across the range of aspect angles of interest, e.g., a conducting sphere and various corner reflectors. |
'Swerling1' | The target is assumed to be made up of many independent scatterers of equal
size. This model is typically used to represent aircraft. The instantaneous RCS
signature value returned by the value method in this case is a random variable
distributed according to the exponential distribution with a mean determined by
the Pattern property. |
'Swerling3' | The target is assumed to have one large dominant scatterer and several
small scatterers. The RCS of the dominant scatterer equals
1+sqrt(2) times the sum of the RCS of other scatterers.
This model can be used to represent helicopters and propeller driven aircraft.
In this case the instantaneous RCS signature's value returned by the value
method is a random variable distributed according to the 4th degree chi-square
distribution with mean determined by the Pattern
property. |
Data Types: char | string
Object Functions
Examples
Specify the radar cross-section (RCS) of a triaxial ellipsoid and plot RCS values along an azimuth cut.
Specify the lengths of the axes of the ellipsoid. Units are in meters.
a = 0.15; b = 0.20; c = 0.95;
Create an RCS array. Specify the range of azimuth and elevation angles over which RCS is defined. Then, use an analytical model to compute the radar cross-section of the ellipsoid. Create an image of the RCS.
az = [-180:1:180]; el = [-90:1:90]; rcs = rcs_ellipsoid(a,b,c,az,el); rcsdb = 10*log10(rcs); imagesc(az,el,rcsdb) title('Radar Cross-Section') xlabel('Azimuth (deg)') ylabel('Elevation (deg)') colorbar

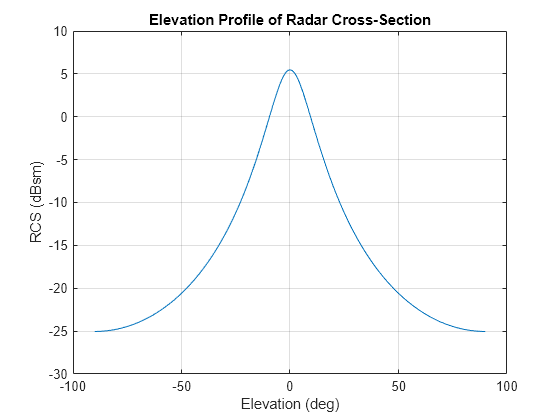
Create an rcsSignature object and plot an elevation cut at azimuth.
rcssig = rcsSignature('Pattern',rcsdb,'Azimuth',az,'Elevation',el,'Frequency',[300e6 300e6]); rcsdb1 = value(rcssig,30,el,300e6); plot(el,rcsdb1) grid title('Elevation Profile of Radar Cross-Section') xlabel('Elevation (deg)') ylabel('RCS (dBsm)')
function rcs = rcs_ellipsoid(a,b,c,az,el) sinaz = sind(az); cosaz = cosd(az); sintheta = sind(90 - el); costheta = cosd(90 - el); denom = (a^2*(sintheta'.^2)*cosaz.^2 + b^2*(sintheta'.^2)*sinaz.^2 + c^2*(costheta'.^2)*ones(size(cosaz))).^2; rcs = (pi*a^2*b^2*c^2)./denom; end
Import the radar cross-section (RCS) measurements of a 1/5th scale Boeing 737. Load the RCS data into an rcsSignature object. Assume the RCS follows a Swerling 1 distribution.
load('RCSSignatureExampleData.mat','boeing737'); rcs = rcsSignature('Pattern',boeing737.RCSdBsm, ... 'Azimuth', boeing737.Azimuth,'Elevation',boeing737.Elevation, ... 'Frequency',boeing737.Frequency,'FluctuationModel','Swerling1');
Set the seed of the random number generator for reproducibility of example.
rng(3231)
Plot sample RCS versus azimuth angle.
plot(rcs.Azimuth,rcs.Pattern) xlabel('Azimuth (deg)'); ylabel('RCS (dBsm)') title('Measured RCS from 1/5th scale Boeing 737 model')

Construct an RCS histogram and display the mean value.
N = 1000; val = zeros(1,N); for k = 1:N [val(k),expval] = value(rcs,-5,0,800.0e6); end
Convert to power units.
mean(db2pow(val))
ans = 406.9799
histogram(db2pow(val),50)
xlabel("RCS (dBsm)")
References
[1] Richards, Mark A. Fundamentals of Radar Signal Processing. New York, McGraw-Hill, 2005.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2018b
See Also
value | toStruct | tsSignature
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)