rotateframe
Quaternion frame rotation
Description
rotationResult = rotateframe(quat,cartesianPoints)quat. The elements of the quaternion are normalized before
use in the rotation.
Examples
Input Arguments
Output Arguments
Algorithms
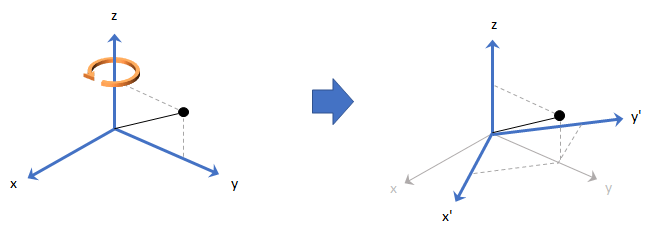
Quaternion frame rotation re-references a point specified in R3 by rotating the original frame of reference according to a specified quaternion:
where q is the quaternion, * represents conjugation, and u is the point to rotate, specified as a quaternion.
For convenience, the rotateframe function takes a point in R3 and returns a point in R3. Given a function call with
some arbitrary quaternion, q = a + bi +
cj + dk, and arbitrary coordinate, [x,y,z],
point = [x,y,z]; rereferencedPoint = rotateframe(q,point)
rotateframe function performs the following operations:
Converts point [x,y,z] to a quaternion:
Normalizes the quaternion, q:
Applies the rotation:
Converts the quaternion output, vq, back to R3
Extended Capabilities
Version History
Introduced in R2018b


