Specify GJR Models
Default GJR Model
The default GJR(,) model in Econometrics Toolbox™ has the form
,
with Gaussian innovation distribution and
.
The default model has no mean offset, and the lagged variances and squared innovations are at consecutive lags. The indicator function equals 1 if and 0 otherwise. For more details on GJR models, see What Is a GJR Model?
You can specify a model of this form using the shorthand syntax gjr(P,Q). For the input arguments P and Q, enter the number of lagged conditional variances (GARCH terms), , and lagged squared innovations (ARCH and leverage terms), , respectively. The following restrictions apply:
and must be nonnegative integers.
If , you must also specify .
When you use this shorthand syntax, gjr creates a gjr model object with these default property values.
Property | Default Value |
|---|---|
| Number of GARCH terms |
| Number of ARCH and leverage terms |
|
|
|
|
| Cell vector of |
| Cell vector of |
| Cell vector of |
|
|
To assign nondefault values to any properties, you can modify the created model using dot notation.
For example, use gjr to create the GJR(1,1) model
,
with Gaussian innovation distribution and
.
Mdl = gjr(1,1)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: 0
The returned model Mdl has NaNs for all model parameters. A NaN value signals to object functions, such as estimate, that a parameter needs to be estimated or otherwise specified by you. You must specify all parameters to, for example, forecast or simulate the model using forecast or simulate.
To estimate parameters, input the model and data to the estimate function. This function returns a fitted gjr model object. The properties of the fitted model contain parameter estimates for the corresponding NaN values of the input model.
When you call gjr without specifying input arguments, gjr returns a GJR(0,0) model object containing default property values. Inspect the default values of a default gjr model object.
DefaultMdl = gjr
DefaultMdl =
gjr with properties:
Description: "GJR(0,0) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
Q: 0
Constant: NaN
GARCH: {}
ARCH: {}
Leverage: {}
Offset: 0
Create GJR Model By Using Shorthand Syntax
Use the shorthand gjr(P,Q) syntax to create the GJR(1,1) model
,
with a Gaussian innovation distribution and
Mdl = gjr(1,1)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: 0
The output shows that the model Mdl has NaN values for these model parameters:
Constant— the conditional variance model constant termGARCH— the lag 1 GARCH coefficientARCH— the lag 1 ARCH coefficientLeverage— the lag 1 leverage coefficient
The default innovation model offset, specified by Offset, is 0.
You can modify the model by using dot notation or by passing it and data to the estimate function.
Using Name-Value Arguments
The most flexible way to specify GJR models is using name-value arguments. You do
not need, nor are you able, to specify a value for every model property.
gjr assigns default values to any model properties you do not
(or cannot) specify.
The general GJR(P,Q) model is of the form
where and
The innovation distribution can be Gaussian or Student’s t. The default distribution is Gaussian.
In order to estimate, forecast, or simulate a model, you must specify the parametric form of the model (e.g., which lags correspond to nonzero coefficients, the innovation distribution) and any known parameter values. You can set any unknown parameters equal to NaN, and then input the model to estimate (along with data) to get estimated parameter values.
gjr (and estimate) returns a model corresponding to the model specification. You can modify models to change or update the specification. Input models (with no NaN values) to forecast or simulate for forecasting and simulation, respectively. Here are some example specifications using name-value arguments.
| Model | Specification |
|---|---|
| gjr('GARCH',NaN,'ARCH',NaN,... or gjr(1,1) |
| gjr('Offset',NaN,'GARCH',NaN,... |
| gjr('Constant',0.1,'GARCH',0.6,... |
Here is a full description of the name-value arguments you can use to specify GJR models.
Note
You cannot assign values to the properties P and Q. egarch sets P equal to the largest GARCH lag, and Q equal to the largest lag with a nonzero squared innovation coefficient, including ARCH and leverage coefficients.
Name-Value Arguments for GJR Models
| Name | Corresponding GJR Model Term(s) | When to Specify |
|---|---|---|
Offset | Mean offset, μ | To include a nonzero mean offset. For example, 'Offset',0.2. If you plan to estimate the offset term, specify 'Offset',NaN.By default, Offset has value 0 (meaning, no offset). |
Constant | Constant in the conditional variance model, κ | To set equality constraints for κ. For example, if a model has known constant 0.1, specify 'Constant',0.1.By default, Constant has value NaN. |
GARCH | GARCH coefficients, | To set equality constraints for the GARCH coefficients. For example, to specify a GJR(1,1) model with specify 'GARCH',0.6.You only need to specify the nonzero elements of GARCH. If the nonzero coefficients are at nonconsecutive lags, specify the corresponding lags using GARCHLags.Any coefficients you specify must satisfy all stationarity constraints. |
GARCHLags | Lags corresponding to the nonzero GARCH coefficients | GARCHLags is not a model property.Use this argument as a shortcut for specifying GARCH when the nonzero GARCH coefficients correspond to nonconsecutive lags. For example, to specify nonzero GARCH coefficients at lags 1 and 3, e.g., nonzero and specify 'GARCHLags',[1,3].Use GARCH and GARCHLags together to specify known nonzero GARCH coefficients at nonconsecutive lags. For example, if and specify 'GARCH',{0.3,0.1},'GARCHLags',[1,3] |
ARCH | ARCH coefficients, | To set equality constraints for the ARCH coefficients. For example, to specify a GJR(1,1) model with specify 'ARCH',0.3.You only need to specify the nonzero elements of ARCH. If the nonzero coefficients are at nonconsecutive lags, specify the corresponding lags using ARCHLags. |
ARCHLags | Lags corresponding to nonzero ARCH coefficients |
Use this argument as a shortcut for specifying Use |
Leverage | Leverage coefficients, | To set equality constraints for the leverage coefficients. For example, to specify a GJR(1,1) model with specify You only need to specify the nonzero elements of |
LeverageLags | Lags corresponding to nonzero leverage coefficients |
Use this argument as a shortcut for specifying Use |
Distribution | Distribution of the innovation process | Use this argument to specify a Student’s t innovation distribution. By default, the innovation distribution is Gaussian. For example, to specify a t distribution with unknown degrees of freedom, specify To specify a t innovation distribution with known degrees of freedom, assign |
Specify GJR Model Using Econometric Modeler App
You can specify the lag structure, innovation distribution, and leverages of GJR models using the Econometric Modeler app. The app treats all coefficients as unknown and estimable, including the degrees of freedom parameter for a t innovation distribution.
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
In the app, you can see all supported models by selecting a time series variable for the response in the Time Series pane. Then, on the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.
The GARCH Models section contains all supported conditional variance models. To specify a GJR model, click GJR. The GJR Model Parameters dialog box appears.
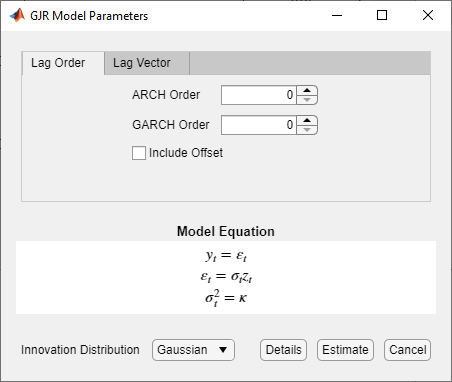
Adjustable parameters include:
GARCH Degree – The order of the GARCH polynomial.
ARCH Degree – The order of the ARCH polynomial. The value of this parameter also specifies the order of the leverage polynomial.
Include Offset – The inclusion of a model offset.
Innovation Distribution – The innovation distribution.
As you adjust parameter values, the equation in the Model Equation section changes to match your specifications. Adjustable parameters correspond to input and name-value pair arguments described in the previous sections and in the gjr reference page.
For more details on specifying models using the app, see Fitting Models to Data and Specifying Univariate Lag Operator Polynomials Interactively.
Specify GJR Model with Mean Offset
This example shows how to specify a GJR(P, Q) model with a mean offset. Use name-value pair arguments to specify a model that differs from the default model.
Specify a GJR(1,1) model with a mean offset,
where and
Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,... 'LeverageLags',1)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: NaN
The mean offset appears in the output as an additional parameter to be estimated or otherwise specified.
Specify GJR Model with Nonconsecutive Lags
This example shows how to specify a GJR model with nonzero coefficients at nonconsecutive lags.
Specify a GJR(3,1) model with nonzero GARCH terms at lags 1 and 3. Include a mean offset.
Mdl = gjr('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1,... 'LeverageLags',1)
Mdl =
gjr with properties:
Description: "GJR(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 3
Q: 1
Constant: NaN
GARCH: {NaN NaN} at lags [1 3]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: NaN
The unknown nonzero GARCH coefficients correspond to lagged variances at lags 1 and 3. The output shows only the nonzero coefficients.
Display the value of GARCH:
Mdl.GARCH
ans=1×3 cell array
{[NaN]} {[0]} {[NaN]}
The GARCH cell array returns three elements. The first and third elements have value NaN, indicating these coefficients are nonzero and need to be estimated or otherwise specified. By default, gjr sets the interim coefficient at lag 2 equal to zero to maintain consistency with MATLAB® cell array indexing.
Specify GJR Model with Known Parameter Values
This example shows how to specify a GJR model with known parameter values. You can use such a fully specified model as an input to simulate or forecast.
Specify the GJR(1,1) model
with a Gaussian innovation distribution.
Mdl = gjr('Constant',0.1,'GARCH',0.6,'ARCH',0.2,... 'Leverage',0.1)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: 0.1
GARCH: {0.6} at lag [1]
ARCH: {0.2} at lag [1]
Leverage: {0.1} at lag [1]
Offset: 0
Because all parameter values are specified, the created model has no NaN values. The functions simulate and forecast don't accept input models with NaN values.
Specify GJR Model with t Innovation Distribution
This example shows how to specify a GJR model with a Student's t innovation distribution.
Specify a GJR(1,1) model with a mean offset,
where and
Assume follows a Student's t innovation distribution with 10 degrees of freedom.
tDist = struct('Name','t','DoF',10); Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,... 'LeverageLags',1,'Distribution',tDist)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model with Offset (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 10
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: NaN
The value of Distribution is a struct array with field Name equal to 't' and field DoF equal to 10. When you specify the degrees of freedom, they aren't estimated if you input the model to estimate.
What Is a GJR Model?
A Glosten-Jagannathan-Runkle (GJR) GARCH model is a type of conditional variance model, a dynamic model that addresses conditional heteroscedasticity, or volatility clustering, in an innovations process εt. Volatility clustering occurs when an innovations process does not exhibit significant autocorrelation, but the variance of the innovations process changes with time and exhibits autocorrelation.
The GJR model is a generalization of the GARCH model that is appropriate for modeling asymmetric volatility clustering [1]. Specifically, the model posits that the current conditional variance is the sum of these linear processes, with coefficients:
Past conditional variances (the GARCH component or polynomial).
Past squared innovations (the ARCH component or polynomial).
Past squared, negative innovations (the leverage component or polynomial).
Conditional Variance Model
Consider the time series
where . Here, zt is an independent and identically distributed series of standardized random variables (Econometrics Toolbox™ supports standardized Gaussian and standardized Student’s t innovation distributions). The constant term, , is a mean offset.
A conditional variance model specifies the dynamic evolution of the innovation variance,
where Ht–1 is the history of the process. The history includes:
Past variances,
Past innovations,
Conditional variance models are appropriate for time series that do not exhibit significant autocorrelation, but are serially dependent. The innovation series is uncorrelated, because:
E(εt) = 0.
E(εtεt–h) = 0 for all t and
However, if depends on , for example, then εt depends on εt–1, even though they are uncorrelated. This kind of dependence exhibits itself as autocorrelation in the squared innovation series,
GJR Model
The GJR model is a GARCH variant that includes leverage terms for modeling asymmetric volatility clustering. In the GJR formulation, large negative changes are more likely to be clustered than positive changes. The GJR model is named for Glosten, Jagannathan, and Runkle [1]. Close similarities exist between the GJR model and the threshold GARCH (TGARCH) model—a GJR model is a recursive equation for the variance process, and a TGARCH is the same recursion applied to the standard deviation process.
The GJR(P,Q) model has P GARCH coefficients associated with lagged variances, Q ARCH coefficients associated with lagged squared innovations, and Q leverage coefficients associated with the square of negative lagged innovations. The form of the GJR(P,Q) model in Econometrics Toolbox is
where and
The indicator function equals 1 if , and 0 otherwise. Thus, the leverage coefficients are applied to negative innovations, giving negative changes additional weight.
For stationarity and positivity, the GJR model has the following constraints:
The GARCH model is nested in the GJR model. If all leverage coefficients are zero, then the GJR model reduces to the GARCH model. This means you can test a GARCH model against a GJR model using the likelihood ratio test.
References
[1] Glosten, L. R., R. Jagannathan, and D. E. Runkle. “On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks.” The Journal of Finance. Vol. 48, No. 5, 1993, pp. 1779–1801.